Sonometro a scala temperata. Seconda parte.
Non rinvenibile negli inventari e di non facile datazione, privo di marca.
Nell`inventario D del 1937 al n° 275 si legge di un altro “Sonometro con due carrucole. ₤ 60” destinato al Gabinetto di Fisica.
Il sonometro non è uno strumento musicale ma serve per costruire le scale musicali e/o per mostrare le leggi dei modi di vibrazione delle corde.
Esso deriva dal monocordo attribuito a Pitagora (560 – 480 a.C.), il quale con questo strumento costruì la prima scala musicale della storia occidentale.
Vastissima è la letteratura al riguardo e secondo alcuni autori, il monocordo era conosciuto ben prima dagli antichi egizi.
Tra gli strumenti a corda la lira fu portata a 7 corde da Terpandro nel VII secolo a.C. e tale rimase per centinaia di anni. Altri autori sostengono che i pitagorici usassero come nota tonica C la frequenza di 256 Hz, ma si ignora come facessero all`epoca a misurare il numero di vibrazioni della corda.
Dunque i greci usavano le lettere del loro alfabeto per chiamare le note (uso rimasto in molti paesi: A (La), B (Si), C (Do) ecc.) e bisogna aspettare fino a Guido D`Arezzo (992-1050) che scelse le prime sillabe dei capoversi di un inno religioso: Ut, Re, Mi, Fa, Sol La. Il Si fu introdotto più tardi ( nota il S. J. finale). UT queant laxis / REsonare fibris / MIra gestorum / FAmuli tuorum /SOLve polluti / LAbii reatum / Sancte Joannes.
La scala di Pitagora, detta melodica, individua ad esempio il Do1 facendo vibrare la corda intera e il Do2, mettendo il ponticello scorrevole nel centro, vedi la figura 1.
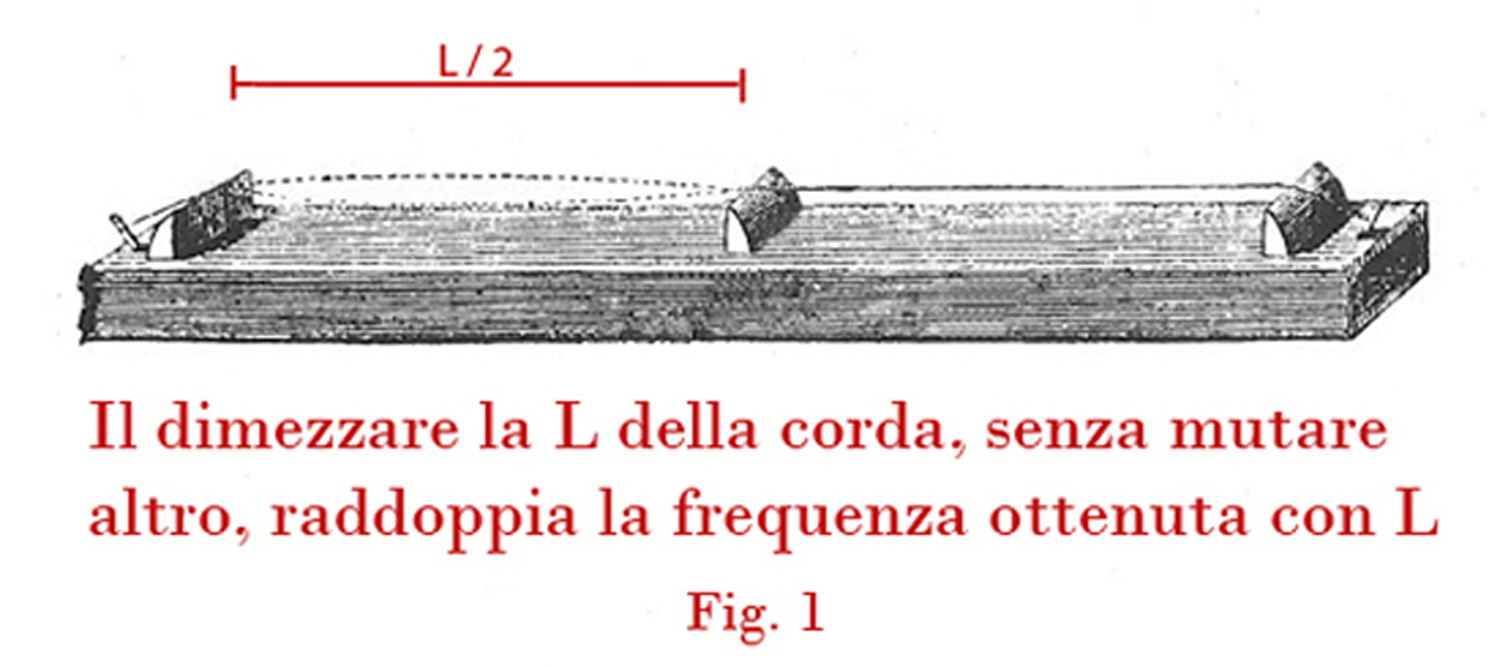
Come si è spiegato nella prima parte, a parità di tensione della corda, con metà lunghezza si ottiene il doppio della frequenza, cioè si passa all`ottava superiore.
Se il ponticello viene posto a 2/3 della lunghezza si ottiene il Sol2 ( vedi la figura 2) che ha una frequenza 3/2 della fondamentale.
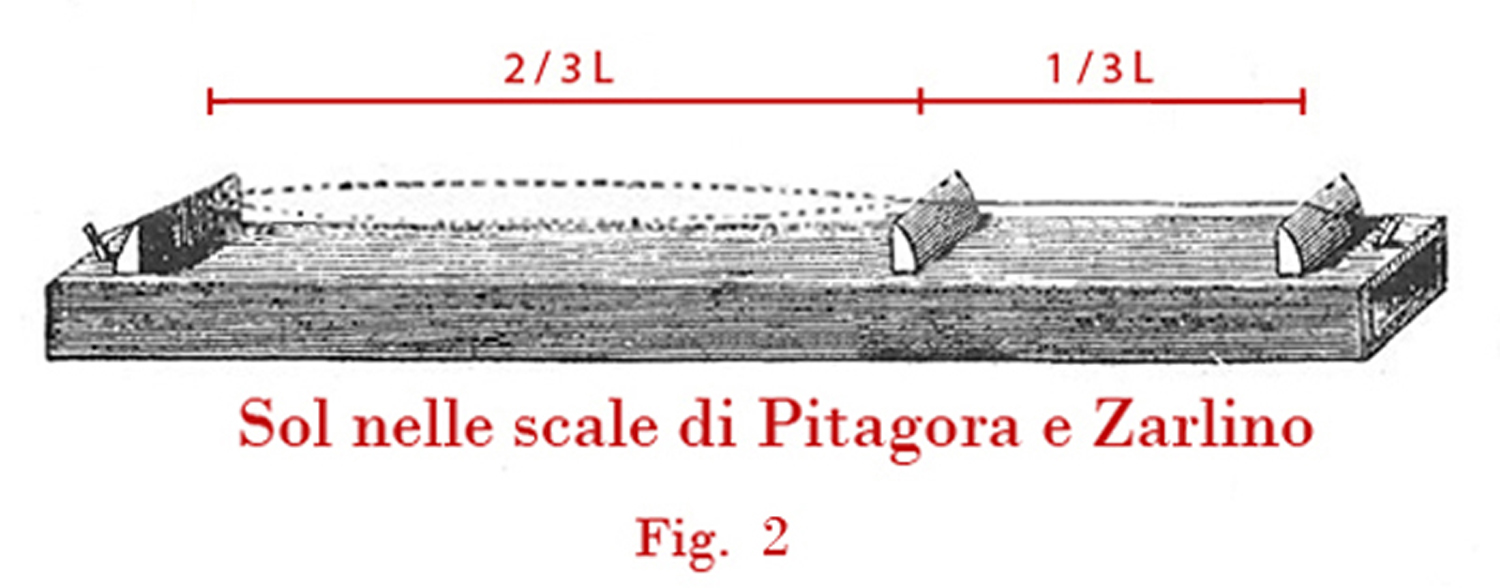Per ottenere le altre note della “gamma” completa si sposta il ponticello su 8/9 L per il Re1 ottenendo una frequenza di 9/8 della fondamentale; così per il Mi1 su 64/81 di L; per il Fa1 3/4 L; per il La1 16/27 L; per il Si1 128/243 L. I rapporti delle frequenze con la fondamentale sono Do1 1; Re1 9/8; Mi1 81/64; Fa1 4/3: Sol1 3/2; La1 27/16; Si1 243/128. Si nota subito che, progredendo, ci si è avvicinati al centro, cioè al Do2.
I suoni sono gradevoli, le frazioni si possono ottenere con combinazioni dei numeri 2 e 3 aventi esponenti 2 3 4 5 6 e i rapporti tra le frequenze di una nota con la precedente sono di 9/8 (tono) o 256/ 243 (semitono), da qui il nome scala diatonica; sembra il trionfo della fisica-matematica che spiega il piacere dell`ascolto, ma le distanze tra le posizioni del ponticello sono irregolari, e dunque gli intervalli tra le note sembrano capricciosi. Inoltre i rapporti di ciascuna nota con la fondamentale sono abbastanza complessi.
Non affrontiamo qui ulteriori problemi relativi a questa scala, a cui ci si riferì fino alla seconda metà del `500.
Dopo un tentativo di semplificare i rapporti, dovuto secondo alcuni a Claudio Tolomeo (87-150 d.C), a partire dal 1558 Gioseffo Zarlino (1517-1590) introdusse la scala armonica con i seguenti rapporti: Do1 1; Re1 9/8; Mi1 5/4; Fa1 4/3; Sol1 3/2; La1 5/3; Si1 15/8; Do2 2.
Essa è detta naturale poiché usa i numeri primi 1 2 3 5 coi loro multipli. Ma mentre nella scala di Pitagora gli intervalli sono tutti uguali, in quella di Zarlino differiscono notevolmente; ciononostante i rapporti di Zarlino erano più adatti per la polifonia e la scala di Pitagora andò in disuso. Per ragioni di spazio non entriamo nei dettagli che sarebbero lunghi e complessi ma invero importanti. L`esigenza di trovare intervalli più regolari tra le note, senza urtare eccessivamente la gradevolezza dei suoni, portò all`introduzione dei bemolle e dei diesis nella scala di Zarlino che dunque si chiamò scala diatonica cromatica (nelle antiche melodie gregoriane il si molle era importante!).
Successivamente, nel tentativo di rendere uguali gli intervalli, si arrivò a concepire di dividere un ottava in 31 parti e nel 1600 fu costruito un organo con 31 tasti per ottava. Si costruirono organi o cembali con 14 o 19 note per ottava, ma la pratica dell`esecuzione risultò difficilissima. Il primo a tentare una soluzione semplificativa ed equilibrata fu Andreas Werckmeinster ( 1645-1706) che nel 1691 introdusse il “buon temperamento”.
Si ritiene che J. S. Bach si sia ispirato ai suoi lavori per il “Clavicembalo ben temperato” scritto in dodici tonalità tra il 1722 e il 1744.
Il temperamento equabile, di cui si è parlato nella prima parte, consiste nel riunire i diesis e i bemolle in una sola nota (i tasti neri del pianoforte) ed è ciò che si vede in questo sonometro.
Nel pianoforte ogni ottava viene suddivisa in dodici intervalli con uguali rapporti e le note sono in progressione geometrica in ragione della radice dodicesima di 2 = 1,05946…. La frequenza di ogni nota e di circa il 6% più alta della precedente. Inizialmente il temperamento equabile fu avversato perché introduce un numero irrazionale e perché esperimenti condotti negli anni con famosi musicisti hanno dimostrato che questi suonano usando la scala cromatica e non quella temperata; ma questa scala comporta notevoli vantaggi pratici come la possibilità di interpretare un brano indipendentemente dalla tonalità scelta, cioè dalla nota che si sceglie come base della scala, inoltre gli strumenti ad intonazione fissa suonano ugualmente bene tutte le tonalità senza bisogno di una riaccordatura totale ecc. .
È bene sottolineare che prima il monocordo e poi il sonometro furono usati per secoli sia come campioni per la costruzione di strumenti sia per l`insegnamento della musica e del canto, fino all`avvento del diapason che, pur essendo stato inventato nel 1711, venne usato come campione solo a partire dal 1831.
Anche la scelta del La3 nei secoli varia da un minimo di 404 Hz del 1699 fino ad un massimo di 452 Hz del 1885. Lo studio della fisica delle corde le cui formule sono riportate nella prima parte si deve a molti scienziati; tra i pionieri più noti vi furono: G. Benedetti (1530-1590); I. Beeckman (1588-1637); M. Mersenne (1588-1648) ; J. Sauver (1653-1716); ma l`elenco sarebbe ben più lungo.
Nell`ottobre del 2014 il Prof. Egisto Mariani ha eseguito un intervento di restauro sul sonometro riportandolo alla funzionalità originaria.
Bibliografia.
Come si è detto la letteratura che riguarda il sonometro è vastissima; noi citeremo solo:
C. Goretti-Miniati, Elementi di Fisica, Vol. II – Parte I, F. Cuggiani, Roma 1909 nel quale sono spiegate dettagliatamente le scale musicali.
H. E. White, Scale e strumenti musicali, 1940 riportato in AA. VV., The Project Physics Course, Zanichelli, Bologna 1977.
Per consultare le altre due parti scrivere “Sonometro” su Cerca.
Foto di Claudio Profumieri, elaborazioni, ricerche e testo di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.