 Sonometro a scala temperata. Prima parte.
Sonometro a scala temperata. Prima parte.
Non rinvenibile negli inventari e di non facile datazione, privo di marca.
Nell`inventario del 1906 al n° 858 di pag. 236 si legge, nella sezione Gabinetto di Fisica, del primo sonometro di cui si ha notizia: “Una cassa lunga di risonanza per tendervi delle corde. In esistenza, condizione mediocre. ₤ 10”.
Il sonometro non è uno strumento musicale per suonare melodie ma serve per costruire e spiegare le scale musicali e/o per mostrare le leggi dei modi di vibrazione delle corde.
Esso deriva dal monocordo attribuito a Pitagora, il quale circa 2500 anni fa con questo strumento costruì la prima scala musicale della storia occidentale.
Secondo alcuni autori, il monocordo era conosciuto ben prima dagli antichi egizi.
Fin dall`antichità era sicuramente noto il fatto che se due suoni hanno uno frequenza doppia dell`altro si ha consonanza. L`intervallo fra i due suoni sarà chiamato in seguito ottava, e questo intervallo è talmente grande che ammette molti suoni intermedi gradevoli.
La scuola pitagorica dunque trasformò il monocordo in uno strumento fisico-matematico per costruire una scala che fu usata fino a circa il 1500; nella seconda parte diamo qualche cenno storico.
Qui descriviamo brevemente questo sonometro.
Una cassa di risonanza in legno lunga 47 cm presenta tre fori per l`uscita del suono; su di essa sono posti due ponti alla distanza di 40 cm.
Da una parte sono fissate due corde metalliche che vengono tese con due ganci, muniti di vite e madrevite, posti dall`altra parte.
È molto importante poter regolare bene la tensione T di ciascuna corda.
In realtà un gancio è andato perduto insieme al ponticello che si fa scorrere sotto le corde per ottenere le lunghezze desiderate. In attesa del restauro le foto sono state elaborate per restituire l`integrità allo strumento.
La corda di maggior diametro è posta sopra una scala musicale temperata che riporta sia le note sia le relative frequenze; l`altra corda più sottile è posta sopra una scala sulla quale è riportata la lunghezza in cm con lo zero a destra e il numero 40 a sinistra.
Lo strumento si eccita o con un archetto di violino o col pizzico, meglio se dato con un plettro.
La scala temperata (o a temperamento equabile) è quella più diffusa in occidente ed ha tutti gli intervalli musicali uguali. Partendo da una nota, scelta come fondamentale, la nota successiva si trova moltiplicando la frequenza della precedente per la radice dodicesima di 2, un numero irrazionale le cui prime cifre sono: 1,0594630945929526182529463.
Per fare un esempio, la prima nota che si legge a sinistra e che corrisponde alla lunghezza massima di 40 cm è il Mi4 di 652 Hz (numero di vibrazioni complete al secondo); moltiplicando 652 per 1,059463 si ottiene 690,76 e infatti poco più a destra, alla distanza di 37,46 cm, si legge 691 corrispondente al Fa4. Moltiplicando 691 ancora per 1,059463 si trova circa 732 che è il Fa4diesis coincidente in questo tipo di scala col Sol4bemolle alla distanza di 35,35 cm. Moltiplicando 732 sempre per 1,059463 si trova circa 776 che è il Sol4 alla distanza di 33,37 cm. e così via. Come si nota subito, i calcoli sono molto approssimati per via del numero irrazionale che da luogo alla progressione geometrica. L`importante è che quando si trova il Mi5 successivo, esso deve avere una frequenza doppia del Mi4, cioè 1304 Hz e deve trovarsi a 20 cm!
È bene sottolineare che questa scala ha come nota fondamentale il La3 di 335 Hz ( il La4 è di 870 Hz), mentre invece tutti gli strumenti musicali moderni, a cominciare dai pianoforti, hanno la scala a temperamento equabile basata sul La3 di 440 Hz (in questo caso il Mi4 vale circa 698,46 Hz). Elenco delle note e delle relative distanze riportate sul sonometro: Mi4 = 652 Hz 40 cm; Fa4 = 691 Hz 37,46 cm; Fa4diesis Sol4bemolle = 732 Hz 35,35 cm; Sol4 = 776 Hz 33,37 cm; Sol4diesis La4bemolle = 822 Hz 31,50 cm; La4 = 870 Hz 29,73 cm; La4diesis Si4bemolle = 922 Hz 28,06 cm; Si4 = 977 Hz 26,48 cm; Do5 = 1035 Hz 25 cm; Do5diesis = 1096 Hz 23,6 cm; Re5 = 1162 Hz 22,3 cm; biquadro = 1220 Hz 21 cm; Mi5 = 1304 Hz 20 cm come si era detto. Si noti come un`ottava è compresa in metà della lunghezza della corda. Fa5 = 1392 Hz 18,5 cm è un dato palesemente errato, poiché 1304 x 1,05946 = 1,3815 Hz che infatti è quasi il doppio di 691! Dunque Fa5 è di 1382 Hz. Proseguendo: 1,3815 x 1,05946 = 1,4636 Hz da cui moltiplicando ancora per 1,05946 si ha circa 1551 Hz che corrisponde al Sol5 ( 776 x 2 = 1552) e non certo 1644 Hz che è il biquadro successivo.
A riprova degli errori scritti nell`ultima parte della scala il La5 deve essere di 1740 Hz, cioè il doppio in frequenza del La4 e dunque, pur con le approssimazioni dei calcoli, il Si5 deve risultare di 1954 Hz e il Do alla fine della scala ha il “giusto” valore 2070 Hz.
Del resto con qualche calcolo si può osservare che i numeri riportati sul sonometro sono arrotondati. Si vuol sottolineare con ciò che le note di ogni ottava successiva devono avere sempre frequenze doppie delle note corrispondenti dell`ottava precedente.
Ovviamente se quelle note non corrispondono alle giuste frequenze, anche le distanze citate non corrispondono.
Tutto ciò fa pensare che questo sonometro non sia mai stato corretto da chi eventualmente lo ha usato in passato. Moltiplicando la lunghezza L della corda per la frequenza f si ottiene la velocità v dell`onda trasversale.
Onda che, viaggiando avanti e indietro nella corda e sovrapponendosi, forma (a causa della permanenza dell`immagine sulla retina dell`occhio) il tipico fuso caratterizzato da un ventre al centro e due nodi ai lati, come si vede nella figura 1.
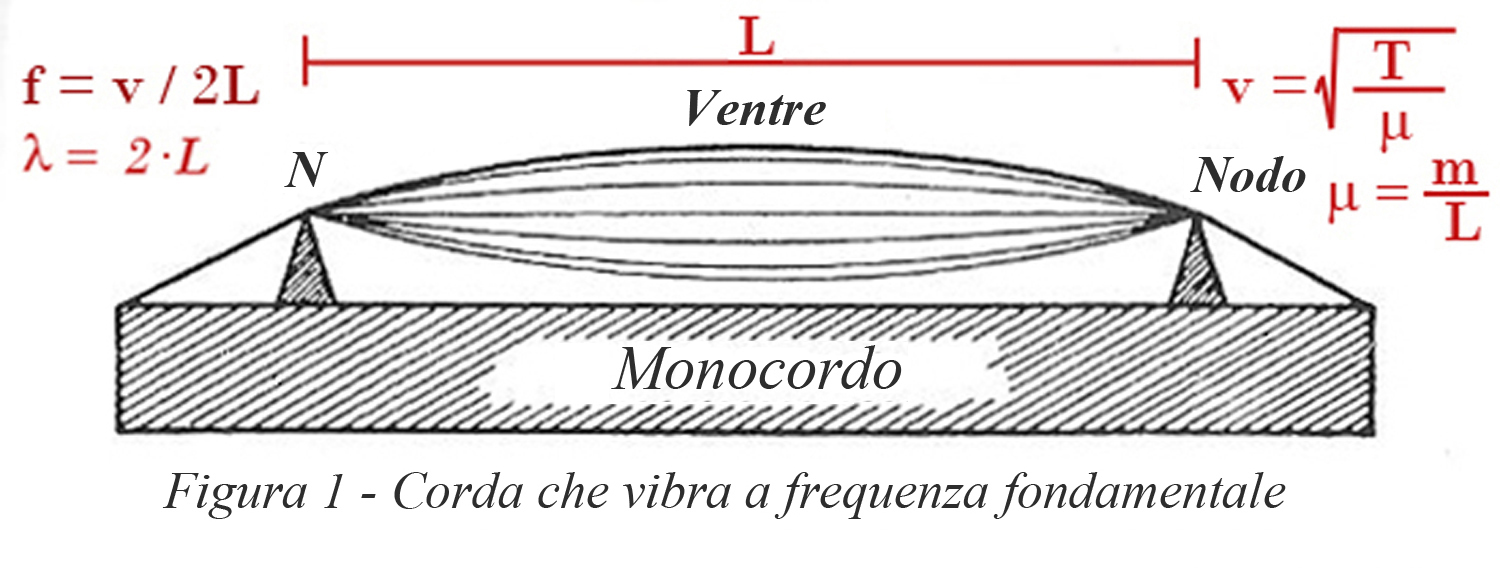
Trascurando le approssimazioni, la velocità dell`onda calcolata si aggira sui 516-517 m/s.
Ormai è diventato chiaro che per ottenere le note segnate sul sonometro bisogna regolare la tensione della corda, confrontando ad esempio il La4 sul sonometro con un diapason (o un diapason elettromagnetico o un campione elettronico) di frequenza 870 Hz, mentre invece storicamente l`uso del sonometro precede l`uso del diapason, che fu inventato da J. Shore nel 1711 e aveva una frequenza di 423,5 Hz.
Didatticamente il sonometro serve anche per mostrare che la frequenza fondamentale del suono emesso dipende dalla lunghezza della corda e dalla velocità di propagazione dell`onda trasversale nella corda secondo la legge f = v / 2L, poiché la condizione di risonanza è che la lunghezza d`onda sia il doppio della lunghezza della corda e questo si ottiene solo per una data velocità.
A sua volta la velocità è uguale alla radice quadrata del rapporto tra la tensione della corda e la massa per unità di lunghezza della corda. Le formule sono in figura 1.
Ecco dunque che per una data sezione di una corda di acciaio e per una data lunghezza, la frequenza del suono dipende dalla radice quadrata della tensione: per raddoppiare la frequenza bisogna quadruplicare la tensione. Inoltre, se la semilunghezza d`onda ad una data frequenza fx è Lx, data la lunghezza L = 40 cm della corda tesa in modo tale che, eccitata con un archetto da violino, vibri all`unisono con un diapason Mi4 di frequenza f = 651,76 Hz, per ottenere la frequenza fx di una nota x si fa scorrere il cavalletto fino a trovare la lunghezza Lx della corda che riproduce il suono della frequenza voluta secondo la formula: fx = (L/Lx) f. Le esperienze e le formule dicono pure che a parità di lunghezza e di tensione e usando corde dello stesso materiale, più sottile è la corda, più acuta è la nota ottenuta: questa è la ragione della presenza della seconda corda.
Nell`ottobre del 2014 il Prof. Egisto Mariani ha eseguito un intervento di restauro sul sonometro riportandolo alla funzionalità originaria.
Bibliografia:
La letteratura sul monocordo e sul sonometro è vastissima.
Noi citeremo solo:
C. Goretti-Miniati, Elementi di Fisica, Vol. II – Parte I, F. Cuggiani, Roma 1909.
H. E. White, Scale e strumenti musicali, 1940, riportato in AA. VV. The Project Physics Course, Zanichelli, Bologna 1977 da cui è tratta la fig. 1.
Per consultare le altre due parti scrivere “Sonometro” su Cerca.
Foto di Claudio Profumieri, elaborazioni, ricerche e testo di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.

