ABSTRACT: Beccaria – Coulomb`s sphere.
Dated 1925, manufactured by “Officine Galileo”, Florence.
The metal sphere is hollow and has got a hole at the top, the supporting stick is made of an insulating resin. Its didactic use is to show that within a conductor there are no electric charges in excess and thus the electric field is zero. To carry out the experimental demonstration it is necessary to charge a little ball made of elder pith hanging to an insulating wire and then to lower the ball through the hole. If the ball keeps inside, its charge shows itself outside the sphere due to electric induction. If the ball comes into contact with the metal, then its charge will be transferred to the outside of the sphere and the ball will discharge. If we introduce once again the little ball inside the sphere , we place it in contact with the internal surface of the sphere and then we pull it out again, we will notice that the little ball has picked up no electric charges. The measurement of electric charges is carried out through an electroscope.
Traduzione di Veronica Rosa, supervisione della prof.ssa Meri Biancucci.
Sfera di Beccaria-Coulomb.
Nell`inventario generale n° 6 del 1925 al n° 2241/140 di pag. 68 si legge: “Officine Galileo Firenze Sfera metallica isolata. ₤ 86”. Destinata al Gabinetto di Fisica. Nell`inventario del 1927 al n° 659 – 2241 si legge di nuovo: “Sfera metallica isolata; ₤ 86”.
Nell`inventario D del 1937 ha il n° 376 dove è detta. “Sfera cava di Coulomb”. Della ditta Officine Galileo Firenze, reca il N° 100281, costo ₤ 80.
La sfera di metallo è cava e presenta un foro sulla sommità, l`astina di sostegno è di resina isolante.
Didatticamente serve per mostrare che all’interno di un conduttore non esistono cariche elettriche in
eccesso e quindi il campo elettrico è nullo, come ci si aspetta dalla comprensione della legge di
Coulomb. Questa è una “prova di zero”, ed ha la sua particolare precisione.
Ne segue che il 2 che compare come esponente di D nella
legge di Coulomb è 2 a meno di una parte su un miliardo; da ciò deriva il secondo nome che usualmente
si da alla sfera. La legge di Coulomb (formalmente analoga a quella di Newton F = G (M m) / D² ) è la seguente:
F = K (Q q) / D².
Dove F è la forza tra due cariche elettriche puntiformi Q e q poste ad una distanza D. K vale 8,987552 109 N m² / C².
Ma la sorprendente analogia tra le due leggi è nel loro aspetto matematico, non nei significati fisici.
Esperimenti più sofisticati hanno confermato la validità della considerazione sull`esponente 2.
L`importanza del valore di questo esponente è legata alla massa che si attribuisce al fotone che, nella fisica moderna, è il messaggero dell`interazione elettromagnetica forte. Una massa nulla significa distanza di interazione infinita e velocità del fotone pari a c nel vuoto, qualunque sia l`energia trasportata.
Se il fotone avesse una massa pur estremamente piccola, la sua velocità sarebbe minore di c e dipenderebbe dalla sua energia: una maggiore energia corrisponderebbe a una maggiore velocità, comunque sempre inferiore a c. Si avrebbero fotoni lenti e fotoni veloci, cioè se una luce bianca partisse ad un dato istante da una sorgente lontanissima, vedremmo prima i colori violetti poi via via arriverebbero tutti gli altri per finire coi i rosso scuri.
Le equazioni di Maxwell sarebbero sostituite dalle equazioni di A. Proca e l`intero Universo sarebbe diverso da quello che conosciam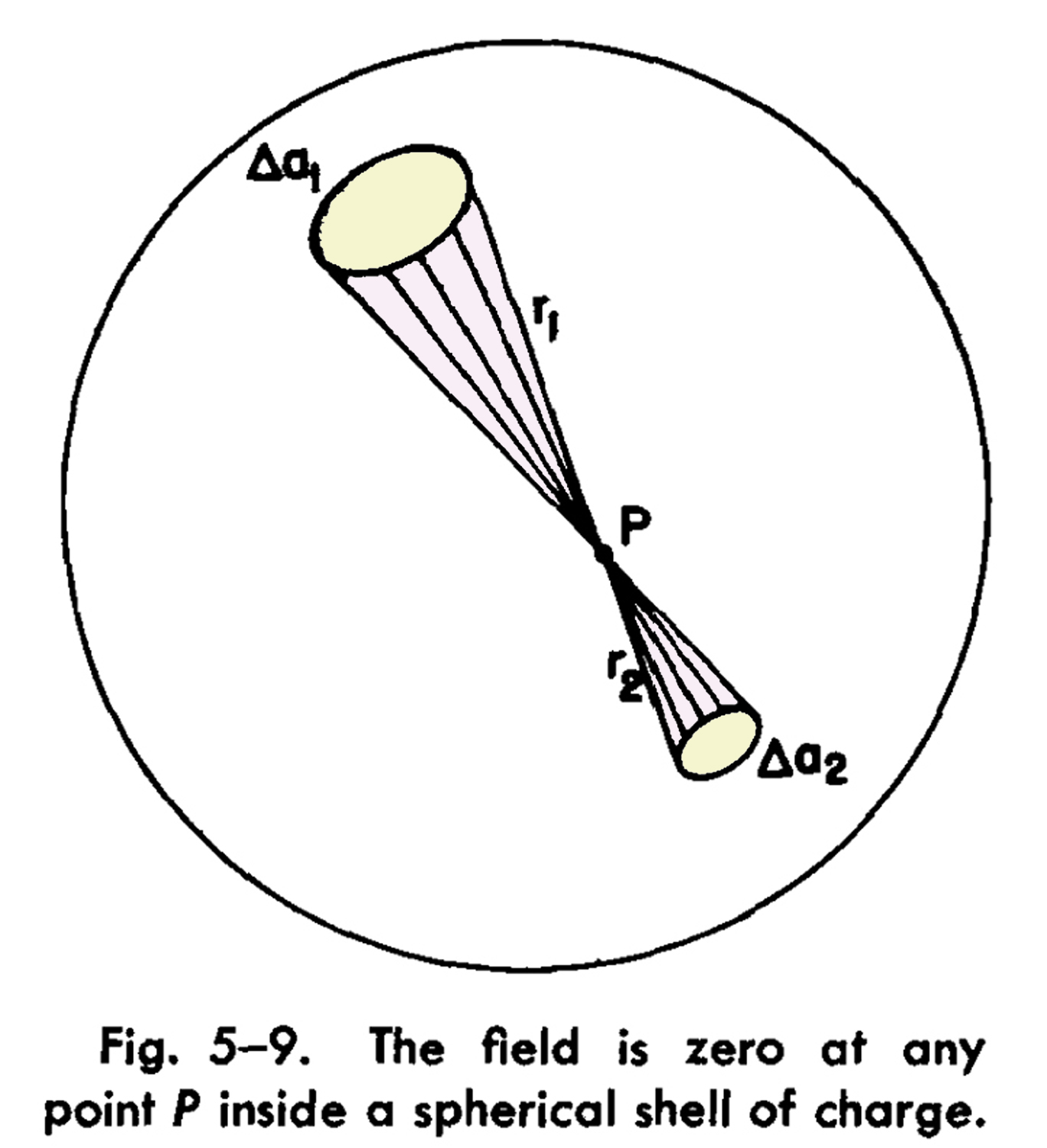o.
Per la dimostrazione sperimentale, dopo aver misurato con l’elettroscopio che la sfera è scarica, si carica una pallina di midollo di sambuco, appesa ad un filo isolante, e la si cala attraverso il foro. Se la pallina staziona all’interno, la sua carica si rivela all’esterno della sfera per induzione elettrica, come si osserva all’elettroscopio.
Se poi la pallina viene posta a contatto col metallo, la sua carica si trasferisce all’esterno della sfera ed essa si scarica, come risulta da una misura successiva con l’elettroscopio.
Introducendo di nuovo la pallina scarica dentro la sfera carica, e mettendola in contatto con la parete interna, alla successiva estrazione si nota che nessuna carica è stata acquisita dalla pallina; mentre l’elettroscopio segna la presenza di cariche sulla superficie esterna della sfera.
In genere gli storici della fisica più noti tendono a trascurare i lavori pionieristici di G. B. Beccaria (1716 – 1781), dunque si legge che fu B. Franklin nel 1755 ad osservare per primo che una sferetta di sughero, posta all`interno di una semisfera cava metallica carica, non viene attratta dalla superficie interna. Franklin ne diede notizia a J. Priestley. Costui nel 1767, per trovare una spiegazione al fenomeno scoperto da Franklin, si ispirò ad un lavoro di Newton sull`assenza di forze di gravità all`interno di un guscio sferico di materiale omogeneo, e dunque ipotizzò che le forze elettriche agiscono con una legge dell`inverso del quadrato della distanza.
Prima di C. A. Coulomb, J. Robison verificò sperimentalmente la legge, ma pubblicò i risultati nel 1881, dopo Coulomb.
Subito dopo nel 1773 H. Cavendish eseguì un esperimento con due sfere metalliche concentriche, collegate con un filo conduttore. Si caricava la sfera esterna, si toglieva il filo tra le due sfere e si misurava la carica sulla sfera interna. Questa è una misura di zero, molto più precisa delle altre. Infatti nel 1936 S. J. Plimpton e W. E. Lawton ripeterono sostanzialmente l`esperimento di Cavendish. Coulomb ebbe i meriti di verificare la legge sia con cariche di segno uguale, sia di segno opposto, a distanze diverse, ottenendo una precisione del 10% peggiore di quelle ottenute da Robison e Cavendish, ma pubblicò i suoi lavori nel 1788, ben prima di loro.
Ma cosa accade se la forma del conduttore cavo non è sferica? Esperienze come il Pozzo e la Gabbia di
Faraday mostrano come la forma può essere qualunque, purché la superficie sia chiusa e che questa non
deve necessariamente essere continua.
Infatti nel caso della gabbia è sufficiente che le maglie della rete siano fitte per ottenere uno schermo elettrostatico. Infine, se il conduttore cavo chiuso viene “messo a
terra”, una qualunque distribuzione di cariche fisse al suo interno non può produrre alcun effetto elettrostatico all’esterno.
Vedremo invece alla voce “Gabbia di Faraday”, nella Sezione Radiotecnica, che ciò non è valido per le cariche in moto nel conduttore o per campi elettrici o elettromagnetici variabili.
Bibliografia.
Gli esperimenti di Coulomb sono descritti in E. Bellone, Storia della fisica moderna e contemporanea, UTET, Torino 1998.
Per una chiara sintesi sia dell`importanza dell`esponente 2, sia della storia di questi esperimenti si consiglia l`articolo di A. S. Goldhaber e M. M. Nieto, La massa del fotone, Le Scienze, settembre 1976.
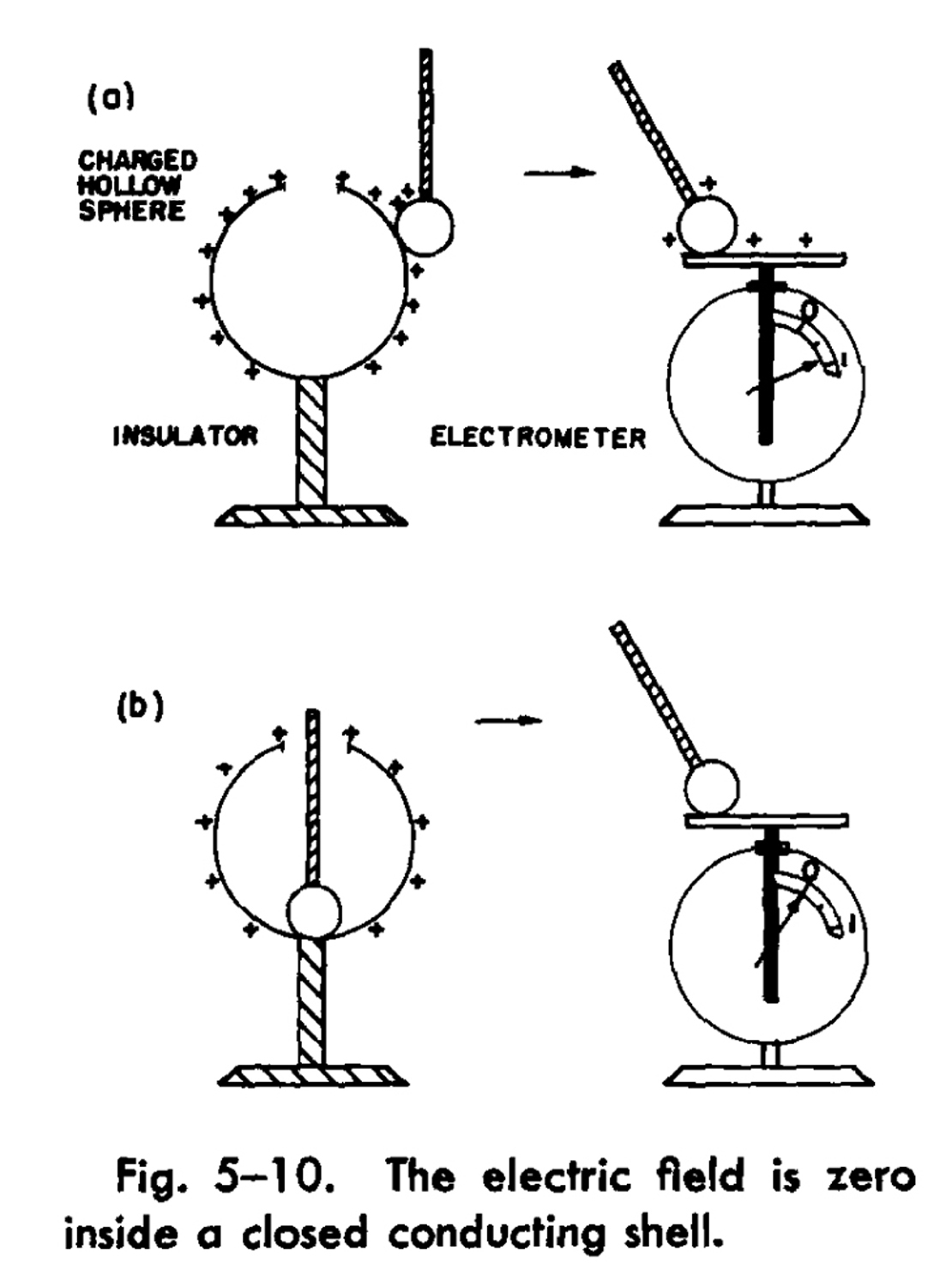
Le figure 5-9 e 5-10 sono state tratte da R. P. Feynman, R. B. Leighton e M. Sands, The Feynman Lectures on Physics, Vol. II, H. Addison – Wesley, P. C. Massachusetts, 1964.
La figura N 1045 è a pag. 249 del catalogo: Apparecchi per
l’Insegnamento della Fisica, a cura del prof. R. Magini, Officine Galileo, 1940.
La sfera è esposta al Museo MITI, su proposta di Fabio Panfili.
Foto di Claudio Profumieri, elaborazioni, ricerche e testo di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.
