PONTE F.A.C.E. STANDARD TIPO 9009-E SERIE N° 9 APP. 212. Seconda parte.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.
Dopo il meticoloso lavoro soprattutto da parte dell’Ing. Claudio Profumieri, del Dott. Paolo Petrelli e con la collaborazione dell’Ing. Marco Rotunno nella ricollocazione di moltissimi strumenti, inventari e manuali di istruzioni, avvenuta nell’anno 2019 in seguito alla chiusura del Triennio, ho ritenuto doveroso provvedere alla pubblicazione di parti dei manuali di istruzioni a corredo delle foto di molti strumenti.
In questo caso particolare ho pensato che le istruzioni d’uso di questo ponte possono contribuire a conservare la conoscenza di alcuni metodi di misura.
Da qui è nata l’idea di trascrivere alla lettera le pagine più interessanti del manuale conservato presso il “piccolo museo ombra”, corredate dalle figure riportate alla loro originalità con un attento lavoro di elaborazione.
Il “piccolo museo ombra” si deve appunto alla necessità di conservare in idonei locali una parte cospicua della strumentazione che prima della chiusura del Triennio era esposta sia negli appositi armadi storici lungo i suoi corridoi, sia presso la sezione Elettronica.
Si vuole qui ringraziare quanti hanno collaborato alla realizzazione di questo luogo, in attesa che un giorno gli strumenti potranno tornare ben visibili laddove erano in precedenza.
§§§§
««…PONTE TRASPORTABILE PER MISURE DI RESISTENZE E LOCALIZZAZIONI F.A.C.E. STANDARD TIPO 9009-E.
Il ponte trasportabile FACE tipo 9009.
GENERALITÀ – Il ponte 9009 e è costituito da una serie di resistenze come i normali ponti di Wheatstone, ma ha, rispetto a questi, il vantaggio di avere incorporato un galvanometro a sospensione (resistenza interna di ca. 250 Ohm – sensibilità di un microampère per ogni divisione della scala) ed un batteria di pile a secco di 4,5 volt. Mediante lo spostamento di apposito commutatore si possono eseguire rapidamente le misure di localizzazione coi metodi di Varley e di Murray.
La batteria a 4,5 Volt può essere facilmente sostituita rimovendo la placchetta segnata con P in fig. 1.
Per misurare resistenze di valore elevato, o per ottenere una maggiore precisione nelle misure, si può sostituire il galvanometro inserendone (fig. 2) uno, di maggiore sensibilità, ai morsetti «GA» nel ponte: a tale scopo basta svitare la vite di fissaggio A per escludere il galvanometro incorporato nel ponte. Analogamente è pure possibile procedere alla inserzione di una batteria esterna di tensione maggiore fra i morsetti «BA» del ponte stesso; in questo caso bisogna escludere la batteria interna spostando nella posizione EST il commutatore «BATT».
Quando si usa una batteria con tensione maggiore di 45 Volt bisogna aggiungere una resistenza esterna di 40 Ohm per ogni volt oltre i 45 sino ad una tensione di 200 Volt che è la massima consentita.
Allo scopo di evitare durante il trasporto dannose oscillazioni all’equipaggio mobile del galvanometro occorre far attenzione che, a coperchio chiuso, l’ago sia bloccato a mezzo dell’apposito fermo.
Il ponte, il cui schema è riportato in fig. 2, consente di eseguire le seguenti misure:
a) resistenza
b) localizzazione di guasti sulle line ( terre o contatti tra fili:
c) localizzazione di interruzioni.
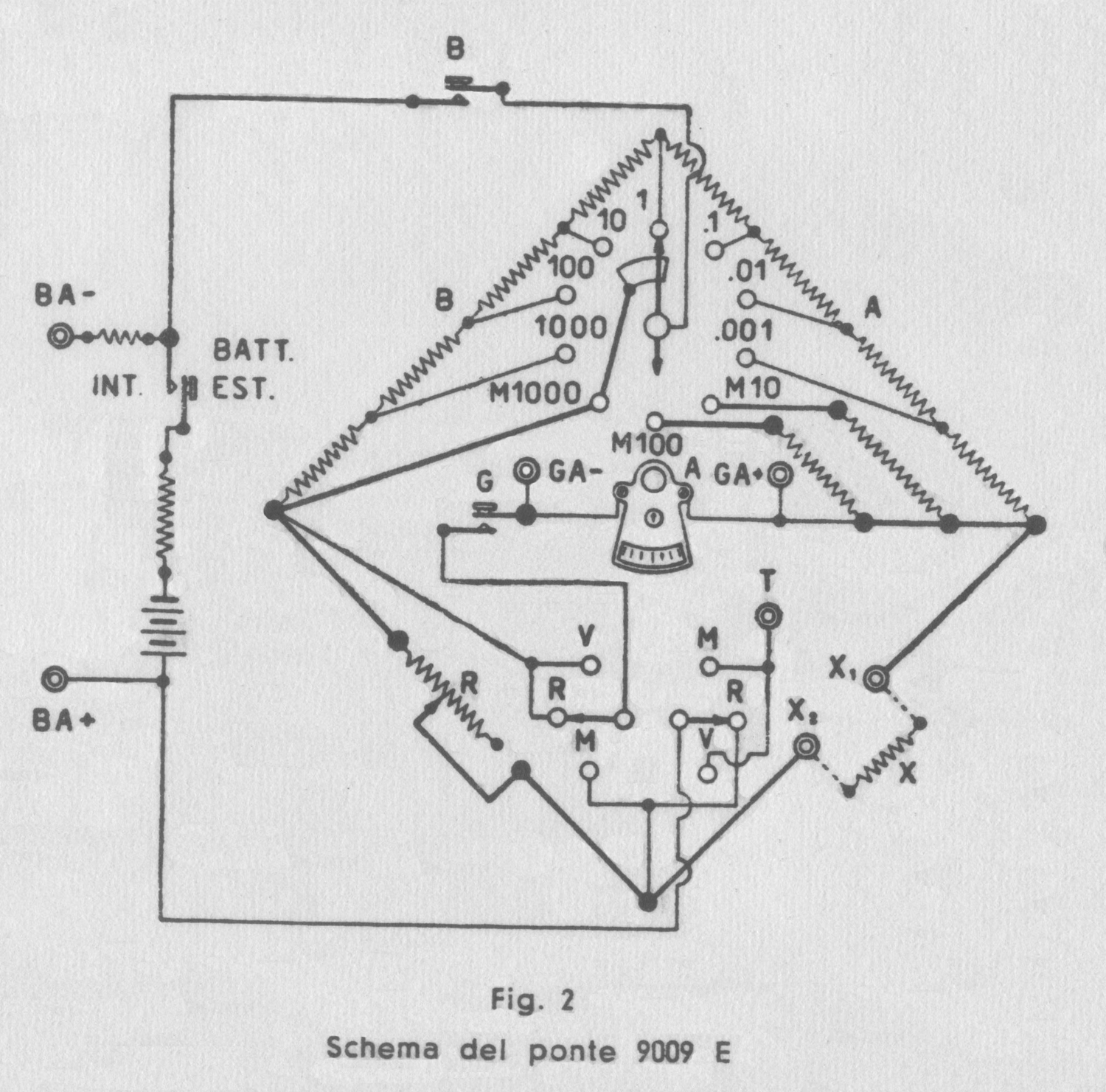
Il ponte può anche usarsi come una normale cassetta di resistenza.
Generalità sulla localizzazione dei guasti
I guasti che si verificano nelle linee di trasmissione si possono suddividere in:
1) Terre: ogni qualvolta si verifica un difetto di isolamento verso terra oppure verso il rivestimento del cavo.
2) Contatti: dovuti a basso isolamento fra conduttori.
3) Interruzioni: dovute a rotture di conduttori ( discontinuità elettrica del circuito).
Allorché tali guasti si verificano, sia su linee terrestri, che su cavi sottomarini di non grande lunghezza, la localizzazione delle prime due categorie ( terre e contatti) si esegue con il ponte di Wheatstone e col metodo detto «del doppino».
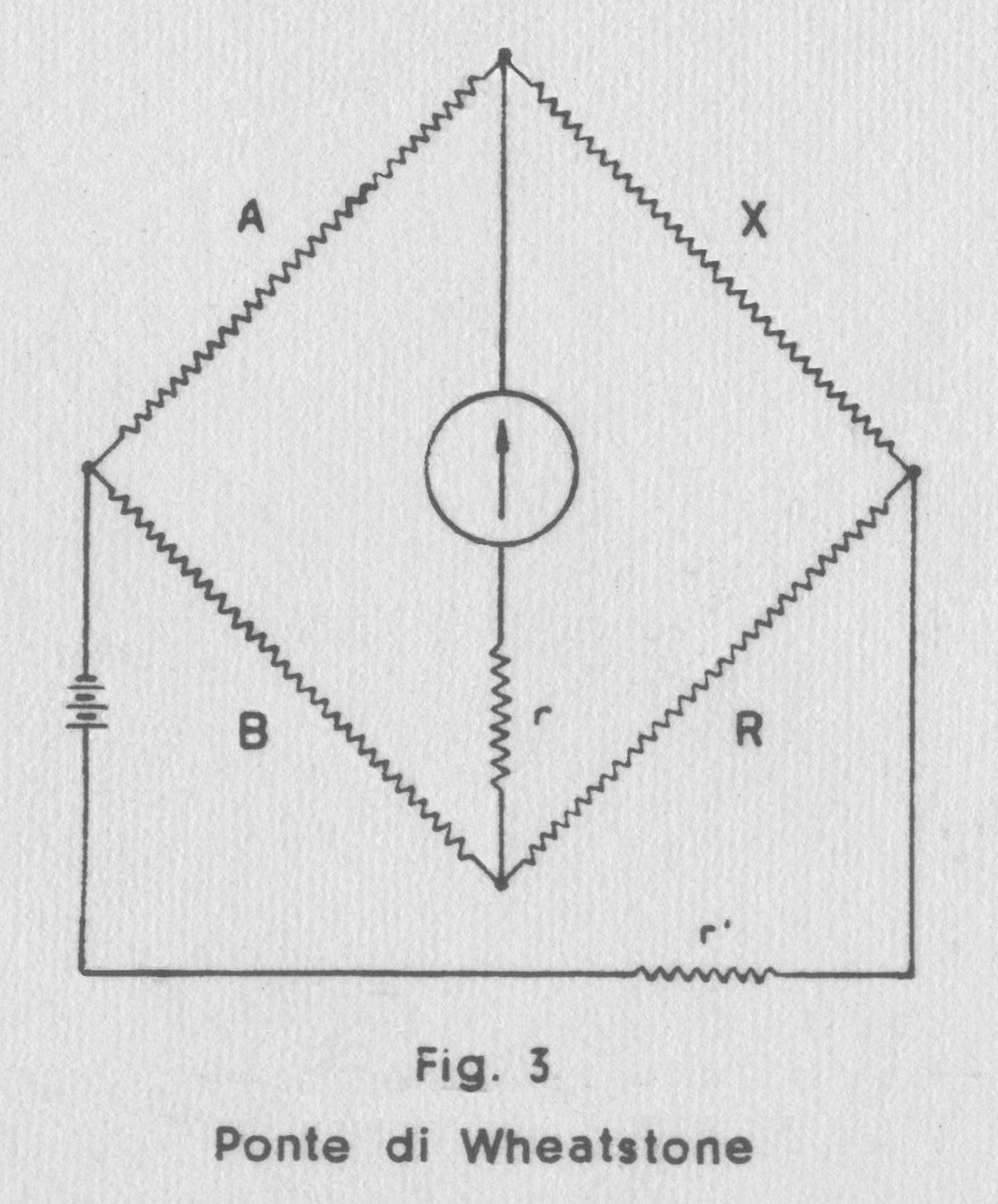
È noto che il ponte di Wheatstone, rappresentato schematicamente in fig. 3, risulta equilibrato (assenza di correnti attraverso il galvanometro) quando fra le 4 resistenze che lo costituiscono (bracci del ponte) è soddisfatta la condizione:
A/B = X/R
Si rammenta che qualunque variazione di resistenza, sia nel circuito del galvanometro che in quello della batteria (schematicamente indicati in fig. 3 con r e r’), non ha influenza sulle condizioni di equilibrio del ponte e che pure immutate permangono le condizioni stesse scambiando fra di loro le batteria e il galvanometro che sono inseriti sulle due diagonali del ponte.
PROVA DEL DOPPINO COL METODO DI MURRAY.
Col metodo di Murray il doppino è costituito dal conduttore guasto e da un conduttore buono uniti fra di loro all’estremo lontano. Il doppino è diviso nel punto del guasto in due parti che costituiscono due bracci del ponte di Wheatstone, mentre gli altri due sono costituiti dalle resistenze del ponte, come mostrato in fig. 4.
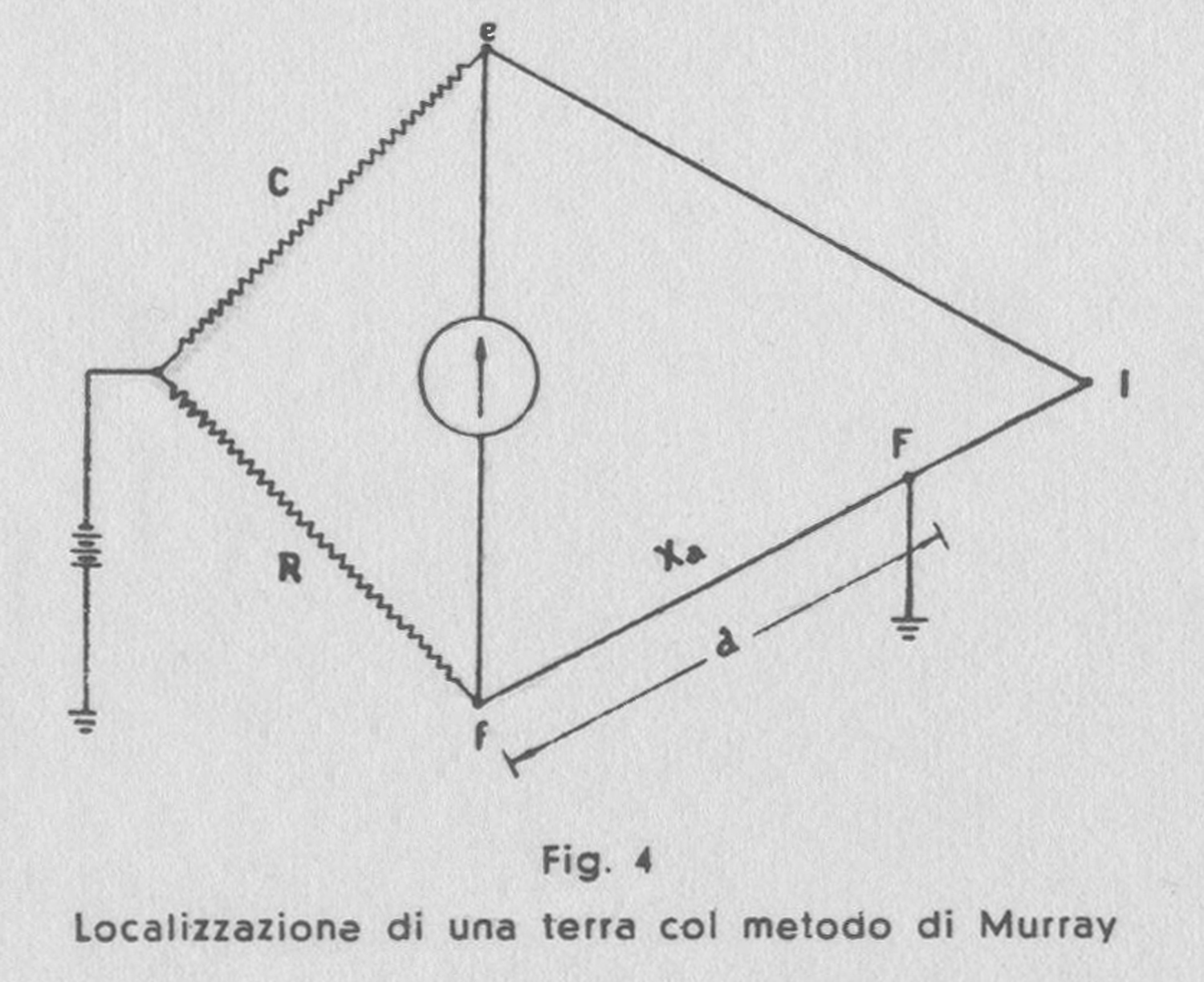In essa fl è il conduttore guasto ed el è quello buono; supposto che il guasto in F sia una terra, si collega F con la batteria mettendo a terra un morsetto della stessa.
Detta X a la resistenza del tratto fF e detta r la resistenza del doppino, il ponte è equilibrato quando:
C/R = (r – X a )/ X a da cui X a = R r / (C+R)
È con quest’ultima espressione che si calcola rapidamente la distanza del guasto dallo strumento allorché si conoscono i valori di C, R, r e il valore della resistenza elettrica per unità di lunghezza dei conduttori in esame.
Quando il conduttore costituente il doppino è di natura e sezione uniforme, le espressioni precedenti assumono una forma più semplice. Infatti, poiché in conduttori di sezione uniforme la resistenza è proporzionale alla lunghezza, detta L la lunghezza totale del doppino e d la distanza del guasto dal morsetto f dell’apparecchio si può scrivere:
C/R = (l – d) / d da cui d = L R/ (C + R)
Ottenendo immediatamente la distanza d.
PROVA DEL DOPPINO COL METODO DI VARLEY:
Il metodo di Varley differisce da quello di Murray per il fatto che una parte del doppino è costituita da una resistenza che si trova nel ponte come indica la fig. 5.
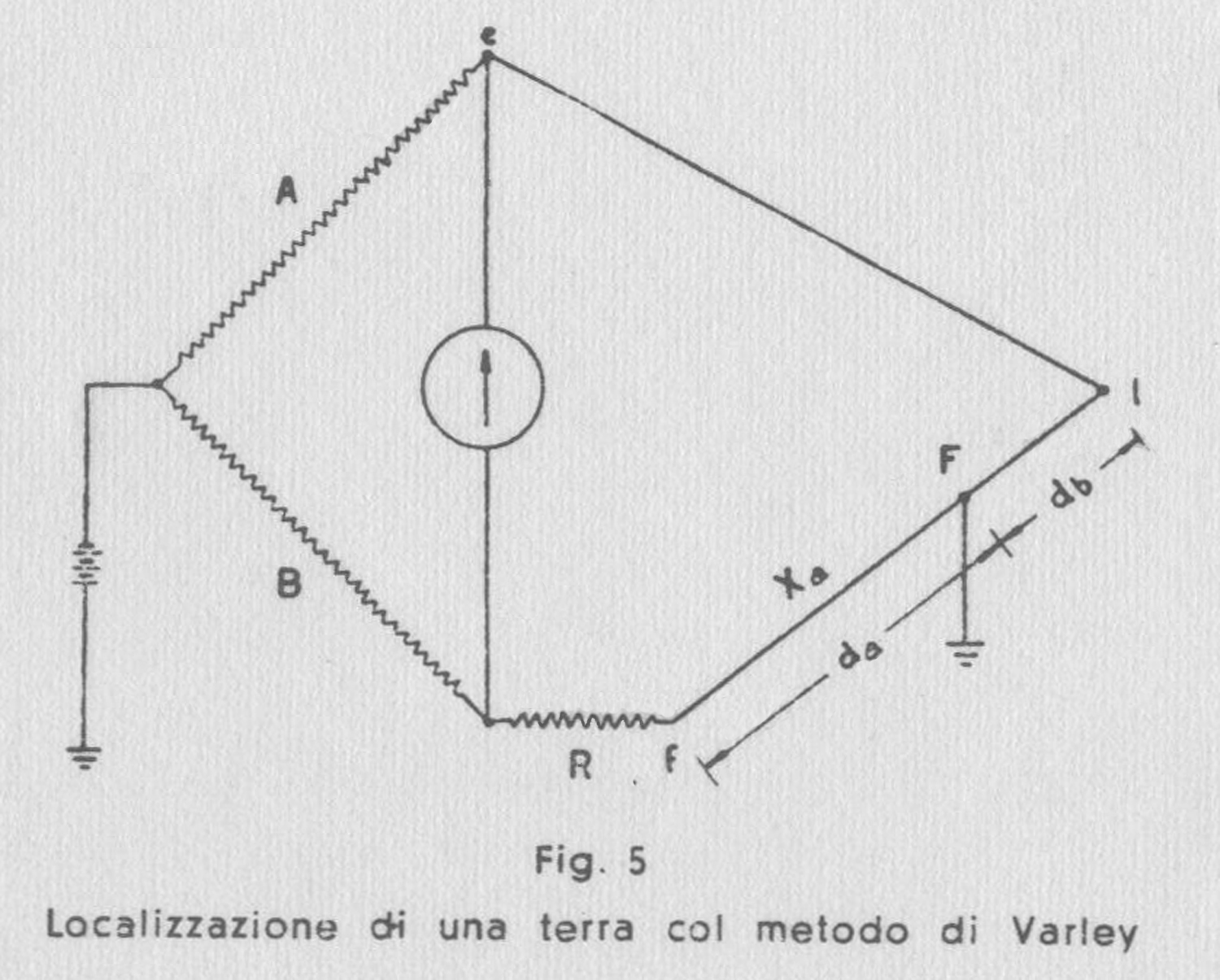
Questo circuito può molto utilmente essere realizzato con quei tipi di ponte che permettono di ottenere rapporti fisi tra A e B come ad es.:
A / B = 1; 10; 100; 1000: ecc.
Con i quali si bilancia il ponte variando R. Inoltre un particolare valore di A / B e precisamente A / B = 1 permette di determinare per due vie diverse e con tutta speditezza la posizione del guasto.
Infatti detta r la somma delle resistenze del conduttore guasto fl e di quello buono el e detta X a la resistenza dal punto f al guasto F, il ponte sarà equilibrato quando:
A / B = (r – X a) / (r + X a) da cui X a = (Br – AR) / A+B
che facendo D = A / B si semplificano nelle:
D = (r – X a) / (R + X a) e X a = (r – DR) / (D + 1)
per D = 1 si ottiene:
X a = (r – R / 2) 1)
Che si può scrivere: R = r – 2 X a
Se la sezione del conduttore del doppino è uniforme, il valore r – 2 X a è il doppio della resistenza del conduttore da F a l.
Per mezzo di questa relazione la distanza del guasto dal punto l si può trovare in due modi diversi e precisamente:
1°) – Quando la linea è uniforme e ne è nota la lunghezza, la distanza db fra il guasto e l’estremo lontano è data dalla:
db = (R/r) L
dove L è la lunghezza del conduttore cioè metà della lunghezza del doppino, mentre r è la resistenza totale del doppino.
ESEMPIO: la resistenza totale r di un doppino in un cavo di 30 km di lunghezza è di 1620 Ohm. La resistenza R del reostato che da la condizione di equilibrio, risulta di 165 Ohm. La distanza del guasto dal punto l è:
db = (165/ 1620) 30000 = 3055,55 m.
2°) – Quando sono note la sezione e la natura del conduttore e ne è incognita la lunghezza, detto s il numero di metri, che nel circuito da l al guasto corrispondono ad 1 Ohm di resistenza, la distanza db del guasto risulta essere:
db = 165 (37,037/2) = 3055,55 m.
Un altro modo di localizzare il guasto col metodo di Varley deriva dalla considerazione che se moltiplichiamo la 1) per s (rappresentando come sopra detto s il numero di metri che nel circuito in esame corrisponde a 1 Ohm di esistenza) si ottiene la distanza da del guasto dall’apparecchio di misura. Si ha:
da = [(r – R) / 2] s 2)
cioè la distanza del guasto dallo strumento si può ottenere moltiplicando la s per la semidifferenza fra la resistenza totale del doppino e la resistenza R del reostato con cui si ottiene l’equilibrio.
La resistenza totale r di un doppino di rame di 9/10 risulta di 1620 Ohm.
L’equilibrio viene raggiunto con un valore della resistenza R di 165 Ohm.
ESEMPIO: la distanza del guasto dell’apparecchio (estremità vicina) usando la 29 risulta:
da = [(1620 – 165) / 2 ] 37,037 = 26.944.42
LOCALIZZAZIONE DELLE INTERRUZIONI NEI CAVI.
La localizzazione delle interruzioni si ottiene con metodi diversi dai precedenti e basati sul fatto che qualunque conduttore, sia che faccia parte di un cavo sotterraneo che sottomarino od aereo, possiede capacità verso i conduttori circostanti per cui è possibile assimilare il sistema ad un condensatore. Il conduttore in prova costituisce una delle armature; l’isolante dal morsetto dell’apparecchio di misura sino all’interruzione costituisce il dielettrico; la terra, l’acqua o la guaina di piombo del cavo costituiscono l’altra armatura.
In un cavo la capacità di un conduttore può ritenersi proporzionale alla lunghezza del conduttore stesso; pertanto una volta determinata la capacità per unità di lunghezza del conduttore, misurando la capacità dello stesso sino all’interruzione, si potrà calcolare la lunghezza del conduttore sino a questo punto. La determinazione di questa capacità si può eseguire prima caricando il conduttore sino a raggiungere un determinato valore della tensione e poi provocando la scarica che viene misurata con un galvanometro balistico.
Questo metodo non è però in pratica conveniente sia per il verificarsi di fenomeni elettrici secondari che complicano l’andamento del fenomeno principale, sia perché la capacità non è, a rigore, uniformemente distribuita su tutta la lunghezza del cavo.
Più semplicemente, per cavi di lunghezza limitata, si può determinare la capacità del conduttore interrotto paragonandola a quella di un conduttore identico, che si trovi nelle stesse condizioni del conduttore in esame e la cui lunghezza sia nota.
A questa determinazione si presta bene lo stesso ponte descritto per la localizzazione delle terre e dei contatti, qualora si sostituiscono la pila con un oscillatore e il galvanometro con un ricevitore telefonico.
Dalla fig. 6 appare che indicando con C1 e C2 le capacità di
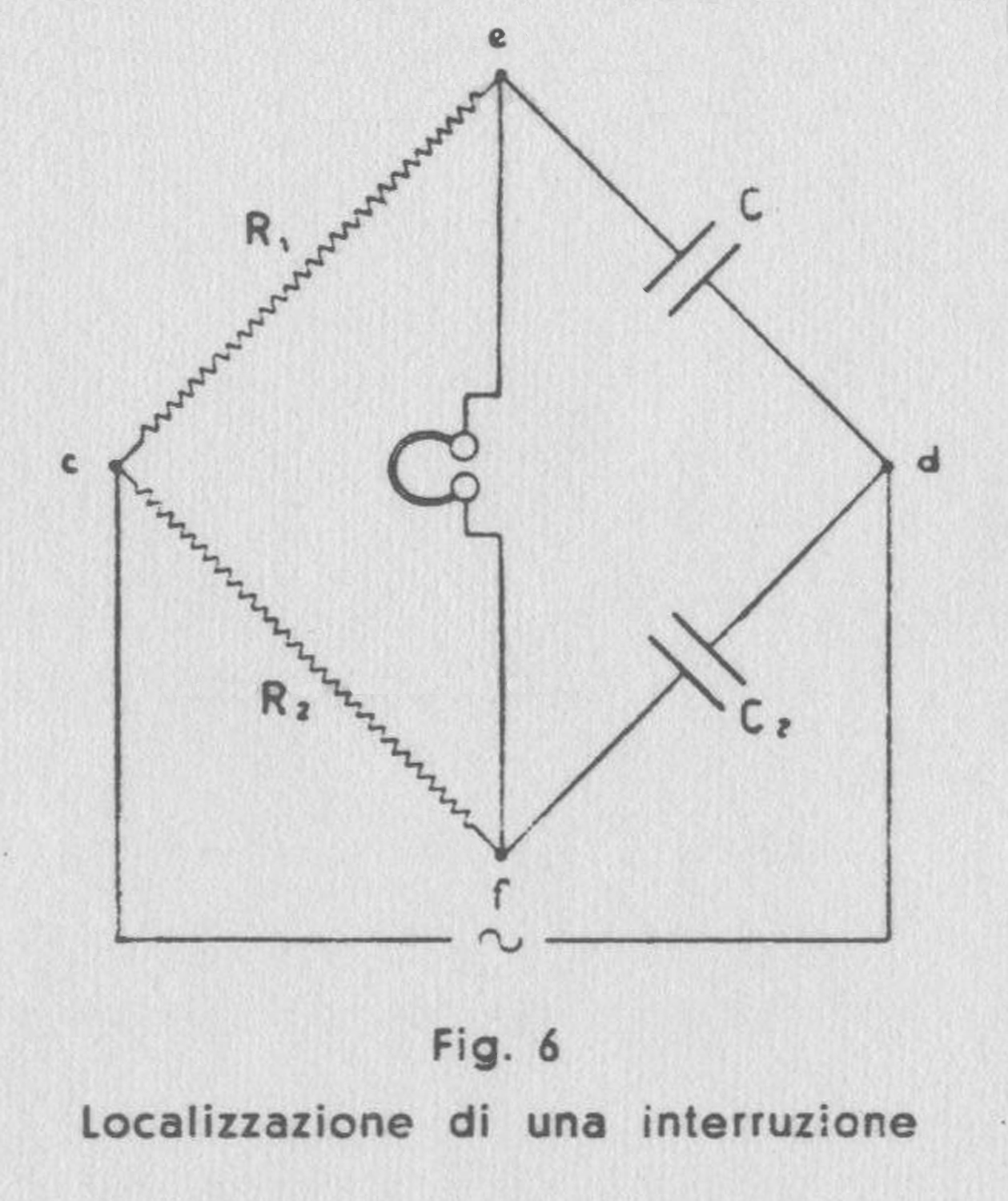
un conduttore interrotto e di un identico conduttore di nota lunghezza è possibile bilanciare queste due capacità variando le resistenze R1 e R2 nelle due altre braccia del ponte sino a non udire più alcun suono nel ricevitore; allora i punti e, f, sono allo stesso potenziale.
I condensatori C1 e C2 hanno uguale tensione e quindi la loro quantità di elettricità è proporzionale alle rispettive capacità.
Ora, poiché la quantità di elettricità che in un certo istante passa attraverso ad un condensatore è direttamente proporzionale alla sua capacità, mentre la quantità di elettricità che passa attraverso una resistenza è inversamente proporzionale alla resistenza stessa, sussiste, a ponte equilibrato, fra le 4 grandezze C1, C2. R1, R2 la seguente relazione:
R2 / R1 = C1 / C2
Sino a che il conduttore guasto e quello efficiente si trovano in analoghe condizioni, le loro lunghezze si possono ritenere proporzionali alle loro capacità. Rappresentando pertanto con d1 e d2 le lunghezze del conduttore difettoso e di quello efficiente si ha:
R2 / R1 = d1 / d2 da cui d1 = R2 / R1 d2
Se equilibrando il ponte non si riesce ad ottenere il silenzio nel ricevitore, è sufficiente determinare il punto di minor intensità del suono. »».
§§§
Per consultare le altre due schede scrivere “9009 E” su Cerca.
Elaborazioni e ricerche di Fabio Panfili.