Categoria: fisica

    Bussola marina Off. Galileo Firenze.
 Nell`inventario D del 1956, al n° 4462 si legge: “Bussola cardanica Galileo”, registrata il 30/12/1968.
 Il Timeo di Platone parla di “pietra eraclea” descrivendo le proprietà magnetiche della pietra di magnesia, detta oggi magnetite (Fe<sub>3</sub> O<sub>4</sub>).  Questa era nota nell`antica Cina, i primi riferimenti molto incerti fanno risalire il suo impiego come bussola per scopi magici fin dall`83 d.C. (Lun Hêng di Wang Chung).
 Sempre in Cina all`epoca Sung (960-1279) fu realizzata una bussola magnetica di cui esiste una descrizione dettagliata nel Wu Ching Tsung Yao di Tsêng Kung-Liang, un libro del 1084. Un pezzetto di ferro magnetizzato, inserito in un pesciolino di legno, era posto a galleggiare in una vaschetta colma d`acqua ad indicare il Sud.
 La tradizione vuole che furono gli occidentali ad usare la calamita come bussola per la navigazione, verso la fine del XII secolo. Secondo alcuni autori fu A. Necham (1157-1217) nel 1180 a parlare dell`impiego degli aghi magnetici per l`orientamento, altri attribuiscono addirittura agli Olmechi la scoperta, risalente in questo caso a circa 3000 anni fa.
  R. Norman, nato forse nel 1550, scoprì che l`ago magnetico, oltre ad orientarsi verso il nord, si inclinava rispetto al piano orizzontale. Per studiare questo comportamento progettò una bussola di inclinazione e pubblicò le sue osservazioni nel The Newe Attractive nel 1581 a Londra.
 Il meridiano magnetico e il meridiano geografico non coincidono e la declinazione magnetica varia da luogo a luogo e nel corso del tempo.
La bussola viene utilizzata per orientarsi, basandosi sulle sue indicazioni e su adatte carte geografiche.
 L`esemplare qui descritto è provvisto della sospensione cardanica che lo rende idoneo all`uso nautico.
Esso è costituito da una cassa cilindrica di metallo la cui parte superiore è di vetro. All`interno della cassa si trova un disco magnetizzato su cui è disegnata la rosa dei venti; al suo centro un cappuccio poggia su un perno e permette al disco di ruotare.
 La sospensione cardanica (dal nome dell`italiano Gerolamo Cardano (1501-1576) ) consente alla bussola di mantenere sempre la sua posizione orizzontale, anche quando è soggetta ad oscillazioni.
A proposito del giunto cardanico bisogna precisare che è già descritto nei Belopoiika di Filone risalenti al III secolo a.C..
  Foto di Claudio Profumieri, elaborazioni, ricerche e testo di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.

 

 

                         Arganetto idraulico.
  Nell`inventario del 1919, a pag. 37 n° 834/12, si trova elencato fra diversi oggetti del Gabinetto di Fisica, il suo costo era di ₤ 25. Ne ignoriamo il costruttore poiché l`oggetto probabilmente è stato riverniciato.
Alcuni autori ne attribuiscono l`invenzione a J. A. Segner (1704 – 1777), che in effetti nella sua turbina ad acqua usò lo stesso genere di ugelli; altri indicano J. T. Desaguliers (1683 – 1744).
 Il suo funzionamento si basa su due principi della fisica: la trasformazione dell`energia potenziale in cinetica e il cosiddetto principio di azione e reazione (che sarebbe meglio chiamare principio di interazione).
Bisogna subito dire che non tutta l`energia potenziale diventa cinetica per le inevitabili perdite e che nella didattica non è molto chiaro cosa si intende per “azione” e per “reazione”.
Il mulinello è costituito da un`ampolla di vetro che viene riempita d`acqua; nella sua parte superiore vi è una tazza di metallo aperta per immettere l`acqua e con un incavo al centro che ben si adatta alla punta conica di una vite fissata sul sostegno che ne regola l`altezza (come si vede in una foto).
Nella sua parte inferiore invece vi è una tazza che presenta quattro tubicini sagomati in modo tale da permettere la fuoriuscita dell`acqua nello stesso verso; anche questa tazza sotto ha un dispositivo per la rotazione dell`ampolla intorno al suo asse di simmetria verticale con attriti molto bassi.
La vite nella parte superiore consente di togliere l`ampolla con facilità dal contenitore di metallo e regola anche la distanza del cono dall`appoggio per una rotazione ottimale. La parte inferiore dell`arganetto è costituita da un contenitore che evita lo spruzzamento dell`acqua nell`ambiente durante la dimostrazione, esso è munito di uno scarico che non fa accumulare il liquido nel contenitore stesso, accumulo che impedirebbe il normale voluto deflusso veloce dell`acqua dai quattro tubicini.
Dunque, per semplificare la spiegazione, trascuriamo sia le perdite di energia sia la velocità di abbassamento del livello superiore dell`acqua contenuta nell`ampolla e affermiamo che l`energia potenziale dell`acqua, dovuta al dislivello tra il pelo libero dell`acqua e gli ugelli di uscita, si trasforma in energia di pressione nella parte più bassa, secondo il noto teorema di Bernoulli sulla conservazione dell`energia per i liquidi ideali in moto stazionario, e ancora che questa energia si trasforma in energia cinetica dando luogo ad una certa velocità di efflusso dell`acqua.
Con queste approssimazioni si potrebbe dire che la velocità di uscita è pari alla radice quadrata di 2 g h, dove g è l`accelerazione di gravità del luogo e h è il dislivello.
A questo dispositivo non si può applicare facilmente il principio della conservazione del momento della quantità di moto poiché la massa dell`intero sistema diminuisce nel tempo, pur senza considerare le perdite per attriti e altri aspetti. Ma, per spiegare “l`azione e la reazione”, consideriamo un intervallo di tempo sufficientemente breve (diremmo meglio infinitesimo) tale da “fingere” di poter trascurare la diminuzione della massa totale d`acqua.
Allora il momento della quantità di moto della massa d`acqua che esce dai quattro tubicini in quell`intervallo di tempo deve equivalere al momento della quantità di moto dell`intera ampolla con il suo contenuto, e dunque quest`ultima deve ruotare in senso opposto al verso della velocità di efflusso dell`acqua per conservare la quantità di moto totale del sistema!
Ulteriore complicazione nel voler applicare il principio della conservazione del momento della quantità di moto vien dal fatto (già suggerito) che la velocità di efflusso nel tempo diminuisce col diminuire del dislivello dell’acqua. Nella realtà, al solito, le cose sono molto più complicate di come apparirebbe solo a vedere l`arganetto in funzione, ma nella scienza le cose vanno sempre così.
Chi parla di scienze esatte, non conosce veramente le scienze.

La figura sopra è tratta da L. Segalin, Fisica sperimentale, Vol. I, G. B. Paravia & C., Torino 1933.

La figura 87718 è a pag. 308 del catalogo Preiliste Nr. 100, Band II. Physikalische Apparate Max Kohl
Chemnitz [1928?], rinvenibile all’indirizzo:
https://vlp.mpiwg-berlin.mpg.de/library/data/lit21057?
Tra quelli riportati dai cataloghi più noti dell’epoca, l’esemplare della Max Kohl è il più somigliante a
questo esemplare.

La figura 140 è a pag. 140 di Elementary Treatise on Phisics Experimental and Applied transalted from
Ganot’s Éléments De Physique by E. Atkinsons, W. Wood & Co. New York 1910, rinvenibile
all’indirizzo:
https://archive.org/details/treatphysics00ganorich .
Nelle ultime due foto i tubicini sembrano mossi poiché l’arganetto è in moto.
Foto di Claudio Profumieri, elaborazioni, ricerche e testo di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.

 

 

 

ABSTRACT: Simple optical Bench. Dates back to the end of the 19th century. It is made up of a support with a graduated pipe along which used to slide four lenses and two little plates, today only three lenses remain. The brass pipe shows etched by hand the number 317. This device was useful to carry out various experiments in the field of geometrical optics.
Traduzione di Luca Ciarrocchi, supervisione di Meri Biancucci.
Banco ottico semplice.
Risalente a fine Ottocento.
Nell’inventario del 1919 al n° 838 di pag. 38 vengono descritti gli oggetti contenuti in un armadio; tra questi si legge: «Supporto con tubo graduato sul quale possono scorrere 4 lenti 2 lastrine, ₤ 100».

Oggi risultano mancanti una lente e le due lastrine che si possono vedere in una foto risalente ai primi anni del Novecento; foto che ritrae il “Gabinetto e scuola di  Fisica e Chimica”.
Altri oggetti visibili nella foto sono elencati come già esistenti nell’inventario del 1906, il più antico di cui disponiamo.
Il tubo in ottone reca inciso a mano il numero 317.
Questo dispositivo era utile per realizzare varie esperienze di ottica geometrica. Ne diamo qui alcuni esempi.
1) Proiettare su uno schermo l`immagine di un filamento di lampadina (o la fiammella di una candela) con una lente convergente; misurare la distanza tra la lente e il filamento e tra la lente e l’immagine sullo schermo, poi ricavare la distanza focale della lente con la formula delle lenti sottili.
2) Misurare l’ingrandimento di una lente convergente; inoltre misurare l’ingrandimento di un sistema formato da due lenti convergenti (obiettivo ed oculare).
3) Trovare sperimentalmente al lunghezza focale di un sistema di due lenti, una convergente e l’altra divergente.
4) Realizzare un cannocchiale astronomico terrestre con una lente divergente (oculare) ed una convergente (obiettivo).
5) Realizzare un cannocchiale astronomico kepleriano con due lenti convergenti.
Lo strumento è esposto al Museo MITI, su proposta di Fabio Panfili.
  Foto di Claudio Profumieri, elaborazioni, ricerche e testo  di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.

 

 

 

 

 

 

 

 

 

 

 

 

Barometro aneroide registratore Richard Frères Paris, N° 11709.
Nell`inventario del 1906, pag. 230, al n° 815 si legge: “Aneroide registratore di Richard con cassetta a giorno”. Brevettato da M. J. Richard il 26 agosto del 1880.
Sulla base è inciso il “marque de fabrique” della ditta “RF.”, con sopra la scritta: “BREVETES SGDG” e sotto si legge: “RICHARD FRÈRES CONSTRUCTEURS BREVETES PARIS 11709”.
L`elemento sensibile è costituito da una serie di otto scatole cilindriche sovrapposte che rendono più sensibile lo strumento alle variazioni della pressione atmosferica rispetto ad un semplice barometro con una sola scatola aneroide (che significa senza liquido). Ogni scatola, da cui è stata tolta l`aria, è a pareti sottili e ondulate e si schiaccia più o meno a seconda della pressione atmosferica. La somma delle flessioni delle singole scatole viene trasmessa ad un indice per mezzo di un sistema di leve, che ne amplifica ulteriormente gli effetti. L`estremità dell`indice porta un pennino carico di inchiostro misto a glicerina per evitarne la rapida essiccazione. Il pennino scrive su un foglio di carta su cui è stampata una quadrettatura con la scala dei valori della pressione atmosferica in funzione del tempo. Un meccanismo ad orologeria muove il cilindro su cui è avvolta la carta, formando un diagramma temporale dell`andamento della pressione atmosferica. La durata della registrazione è di una settimana. Nella cassetta di legno è ben visibile un piccolo termometro. Il barometro registratore è funzionante e in ottimo stato di conservazione.
Bibliografia.
Catalogo, L’Industrie Francaise des Istruments de Precision – Paris 1901 – 1902.
Catalogo, Société A.me des E’.ts J. Richard Ancienne Maison RICHARD Frères, Paris, 1929.
Scheda Ancienne Maison RICHARD Frères Jules Richard del 1931 da cui è tratta la figura di uno dei primi: “Baromètre enregistreur simple” risalente al 1887.
Si può trovare all’indirizzo:
http://cerere.astropa.unipa.it/biblioteca/Strumenti/e-catalogues/Richard1931/Catalogo.html .
L. Segalin, Fisica sperimentale, Vol. I, G. B. Paravia & C., Torino 1933.
Enciclopedia Galileo, Sadea, Firenze 1964.
Lo strumento è esposto al Museo MITI, su proposta di Fabio Panfili.
La foto con il libro antico aperto vicino al barometro è di Daniele Maiani.
Foto di Claudio Profumieri, elaborazioni, ricerche e testo di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.

 

 

 

   Barometro di Fortin Off. Galileo Firenze. Prima parte.
Nell`inventario D del 1956 al n° 3174/5 si legge:  “Barometro di Fortin da parete con nonio 1/20 – destinazione Fisica”. Risulta acquistato il 5 novembre del 1962.
L`etichetta Off. Galileo è incollata sulla parte superiore; il numero di matricola è 0428.
Ma si pensa che sia stato commissionato alla SIAP di Bologna; SIAP è l`acronimo di Società Italiana di Apparecchi di Precisione.
La taratura si riferisce alla temperatura di 0°C e all`accelerazione di gravità di 9,80665 m/s².
Le due scale di misura, incise sui bordi di una fenditura praticata longitudinalmente sul tubo di custodia, vanno da 800 a 1130 mB a destra e da 600 a 850 mm di mercurio a sinistra, in modo tale che l`apparecchio possa servire fino al 2000 m di altitudine. La temperatura di esercizio va da  -10°C a + 50°C.
L`altezza del tubo contenente la colonnina di mercurio è di circa 87 cm, misurato dal pelo libero del mercurio nel pozzetto inferiore.
Esistono al Montani due copie di un libretto di istruzioni dettagliatissime che sono della S.I.A.P. di Bologna, coincidenza vuole che i disegni e i particolari tecnici corrispondono a questo esemplare.
Questo tipo di barometro fu perfezionato da N. Fortin (1750 – 1831) all`incirca nel 1810 ed è una variante più sofisticata del barometro di Torricelli. Esso è trasportabile se si prendono opportune cautele descritte nel libretto di istruzioni e va appeso alla parete verticalmente.
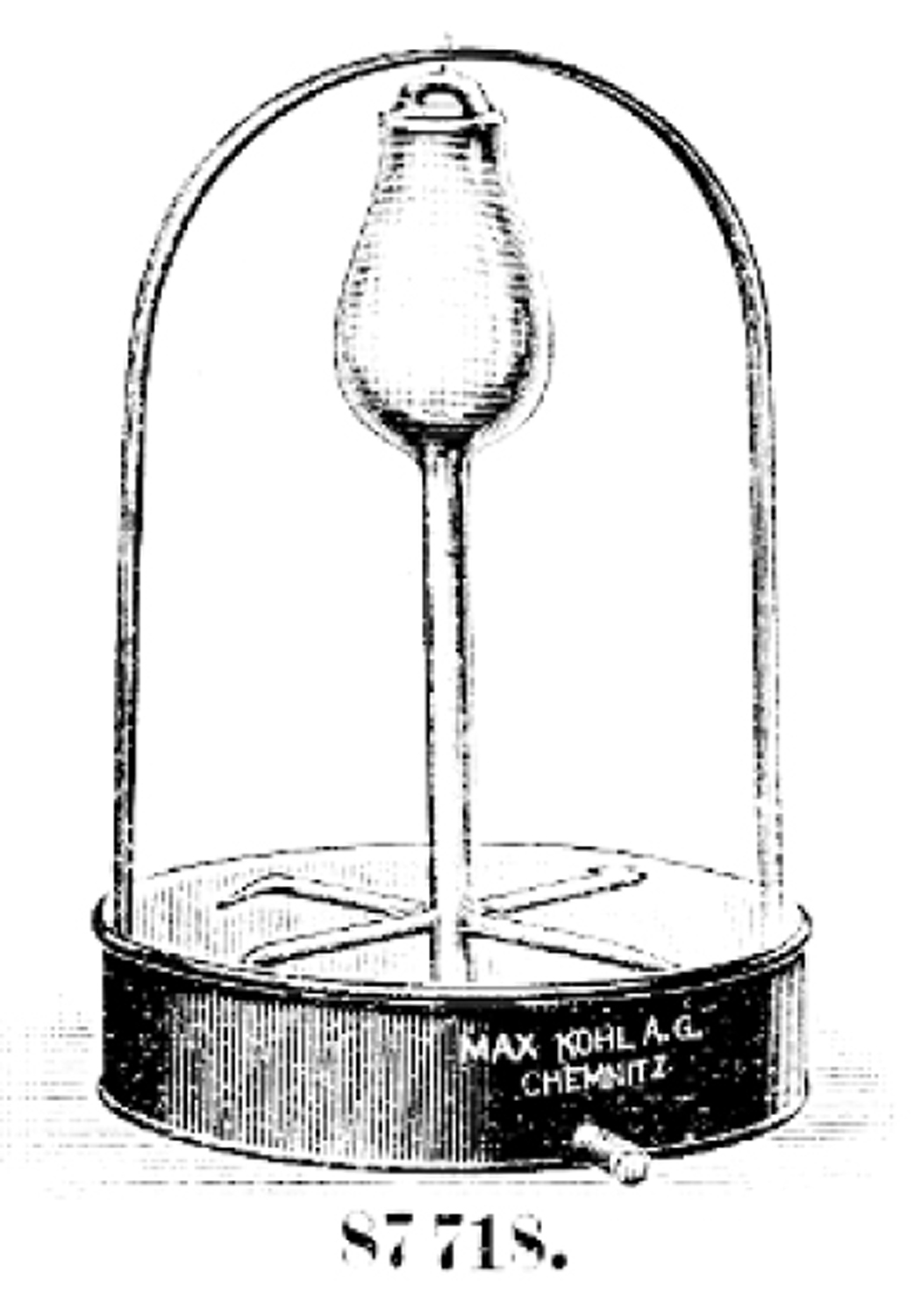
Il primo barometro della storia si deve a G. Berti (1600 – 1643) che nel 1640 usò un tubo di piombo lungo circa undici metri, posto in verticale, chiuso all`estremità superiore e riempito d`acqua che pescava su una vasca anch`essa contenente acqua. Il livello dell`acqua, appena il tubo veniva aperto nella parte inferiore immersa nell`acqua, scendeva a circa nove metri. Siccome nella parte superiore del tubo si veniva a creare un certo grado di vuoto, l`acqua aveva l`inconveniente di evaporare facilmente dando luogo ad una tensione di vapore saturo che faceva abbassare il livello nel tubo (detto livello invece avrebbe dovuto essere intorno ai dieci metri); inoltre vi si instauravano correnti convettive dovute alla differenza di temperatura tra l`acqua nella parte superiore del tubo e quella nella vasca.
Torricelli (1608 – 1647) nel 1643 – 1644 sostituì l`acqua con il mercurio che ha i seguenti vantaggi: la sua densità di circa 13,54 volte quella dell`acqua permette che la lunghezza del tubo si limiti a circa un metro, la sua evaporazione è molto bassa e dunque la tensione di vapore che si ha nella zona superiore del tubo influenza poco la misura. Il livello del mercurio, una volta aperto il tubo nella parte immersa nella vaschetta si porta circa a 760 mm di altezza rispetto alla superficie del mercurio nella vaschetta in determinate condizioni di altitudine, latitudine e temperatura.
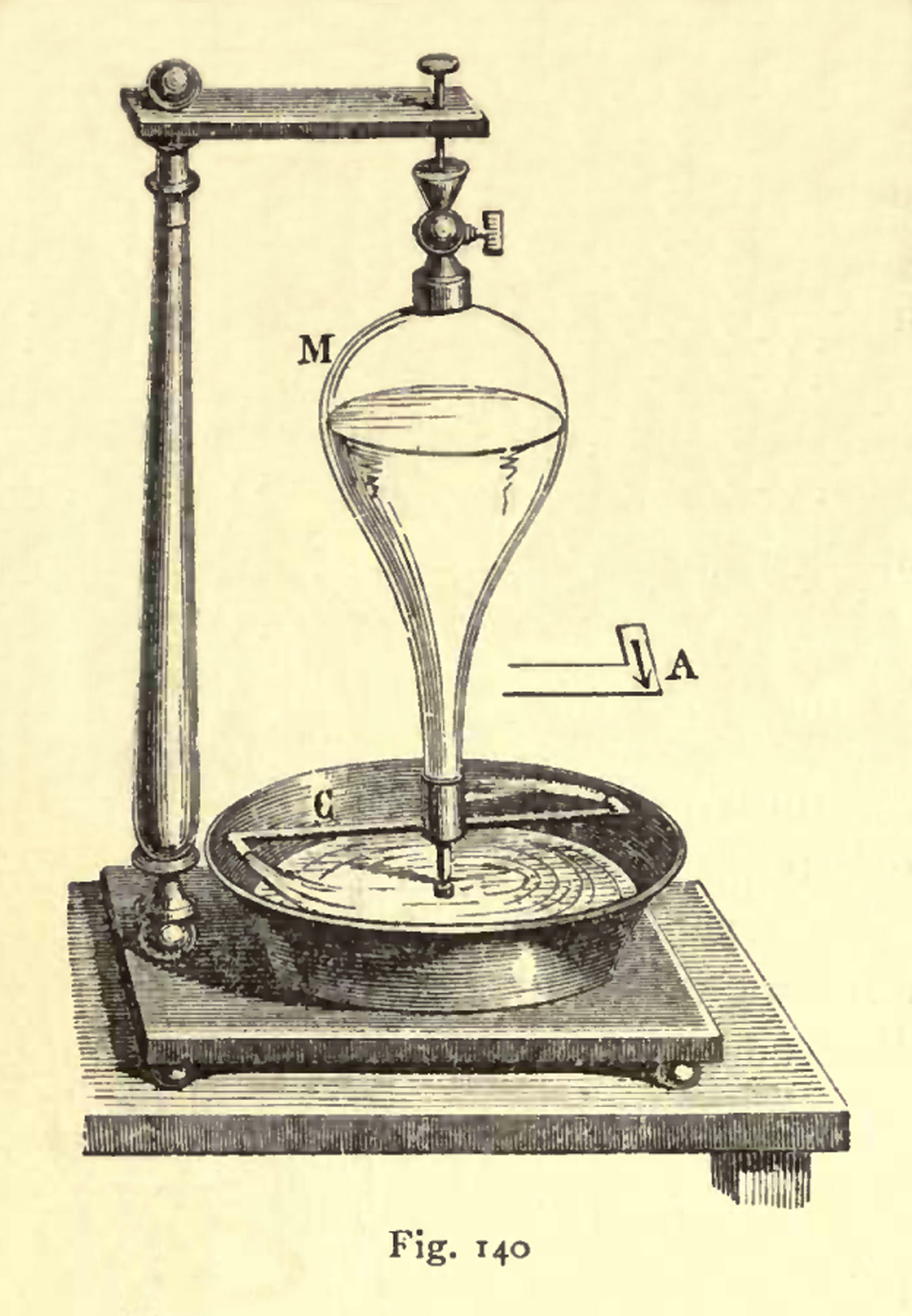
Il funzionamento del barometro di Torricelli (come quello di Berti) si basa sull`equilibrio tra la pressione esercitata dalla colonna di mercurio, presente nel tubo di vetro, sulla superficie interna al tubo a livello della superficie del mercurio nella vaschetta e la pressione atmosferica che agisce sulla superficie libera del mercurio nella vaschetta.
Dunque la pressione p = d g h (dove d è la densità del mercurio, g è l`accelerazione di gravità locale, h è l`altezza raggiunta dal mercurio nel tubo rispetto alla superficie del mercurio nella vaschetta) è in equilibrio con quella esercitata dall`atmosfera sulla superficie del mercurio contenuto nella vaschetta.
Nel barometro di Torricelli il livello del mercurio nella vaschetta, preso come riferimento per le misure di altezza della colonna, varia dunque a seconda della pressione atmosferica, poiché quando la pressione atmosferica è alta spinge maggiore quantità di mercurio nel tubo e il livello in esso sale, ma scende nella vaschetta; viceversa, quando è la pressione è bassa il livello nel tubo scende riversandosi nella vaschetta.

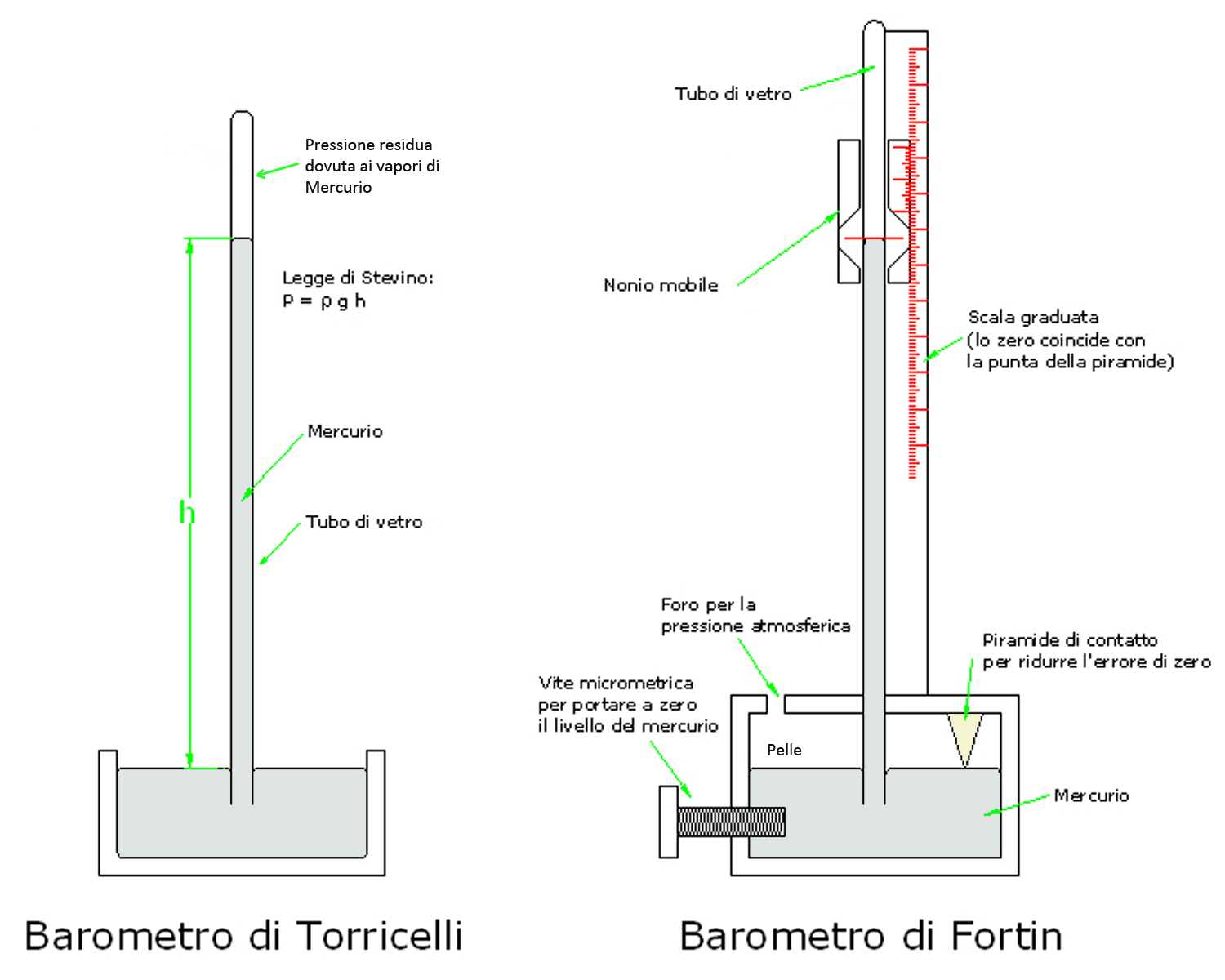
Il barometro Fortin non presenta questo inconveniente per la forma della vaschetta che ha il fondo di pelle il quale si può alzare ed abbassare mediante una vite. Quando il pelo libero del mercurio sfiora una punta conica rivolta verso il basso lo strumento è tarato. La lettura è agevolata da un nonio ventesimale, ma per avere una buona precisione nella misura bisogna apportare (a meno che non si conosca con precisione l`accelerazione di gravità locale) correzioni gravimetriche dovute all`altezza rispetto al livello del mare medio, correzioni gravimetriche dovute alla latitudine; inoltre bisogna apportare correzioni dovute alla temperatura che influenza il volume del mercurio, ciò spiega la presenza del termometro.

Nella seconda parte vi sono le istruzioni della SIAP che riportiamo solo nelle parti essenziali per una spiegazione più approfondita. Per consultarla scrivere “Fortin” su Cerca.
Per le correzioni esistono apposite tabelle nel libretto di istruzioni.
Ulteriori disegni esplicativi si trovano nella scheda dedicata la barometro di Torricelli (scrivere “Torricelli” su Cerca).

Le figure 152 e 154 sono alle pagine 155 e 156 di Elementary Treatise on Physics Experimental and Applied transalted from Ganot’s Éléments De Physique by E. Atkinsons, W. Wood & Co. New York 1910; rinvenibile all’indirizzo:
https://archive.org/details/treatphysics00ganorich

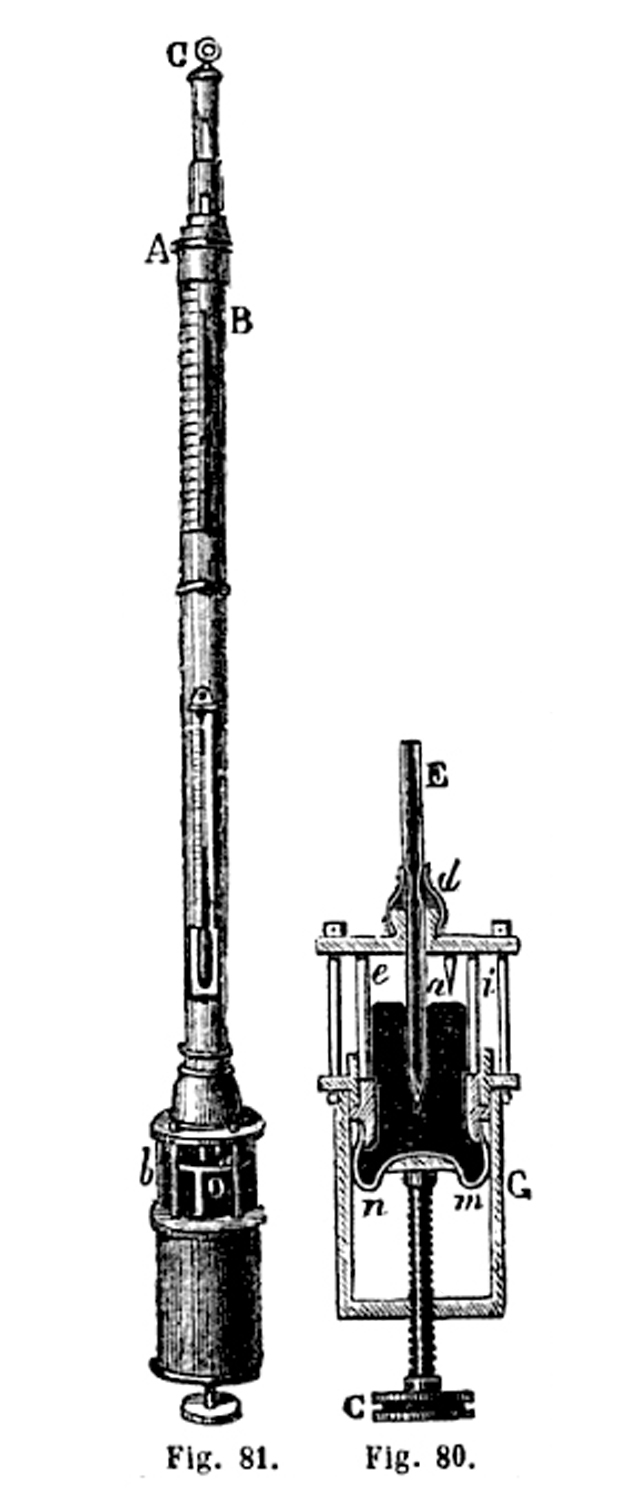
Le figure 80 e 81 sono a pag. 90 di A. Ganot, Trattato Elementare di Fisica Sperimentale ed Applicata, versione di G. Gorini, F. Pagnoni, Milano 1861; rinvenibile all’indirizzo:
https://archive.org/details/bub_gb_1BsQibxllmYC .
Bibliografia: numerosissimi sono il libri su cui trovare sia il barometro di Torricelli sia quello di Fortin.
Un breve ed efficace riassunto storico si trova in M. Guidone, Esiste il vuoto?, Il Montani n° 3-4 dicembre 2000.
Foto di Claudio Profumieri, elaborazioni, ricerche e testo di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.