Categoria: fisica

Aghi magnetici.
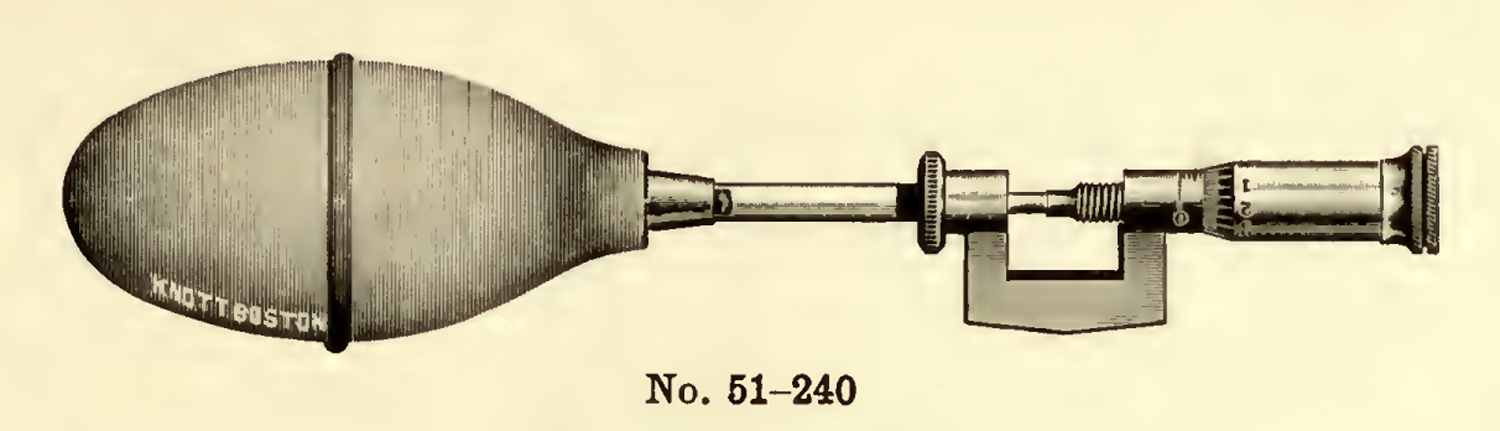
 L`ago magnetico a sostegno curvo, al centro nelle foto, si trova elencato nell`inventario del 1923 al n° 1078/121, ed è riconoscibile per questa sua caratteristica.
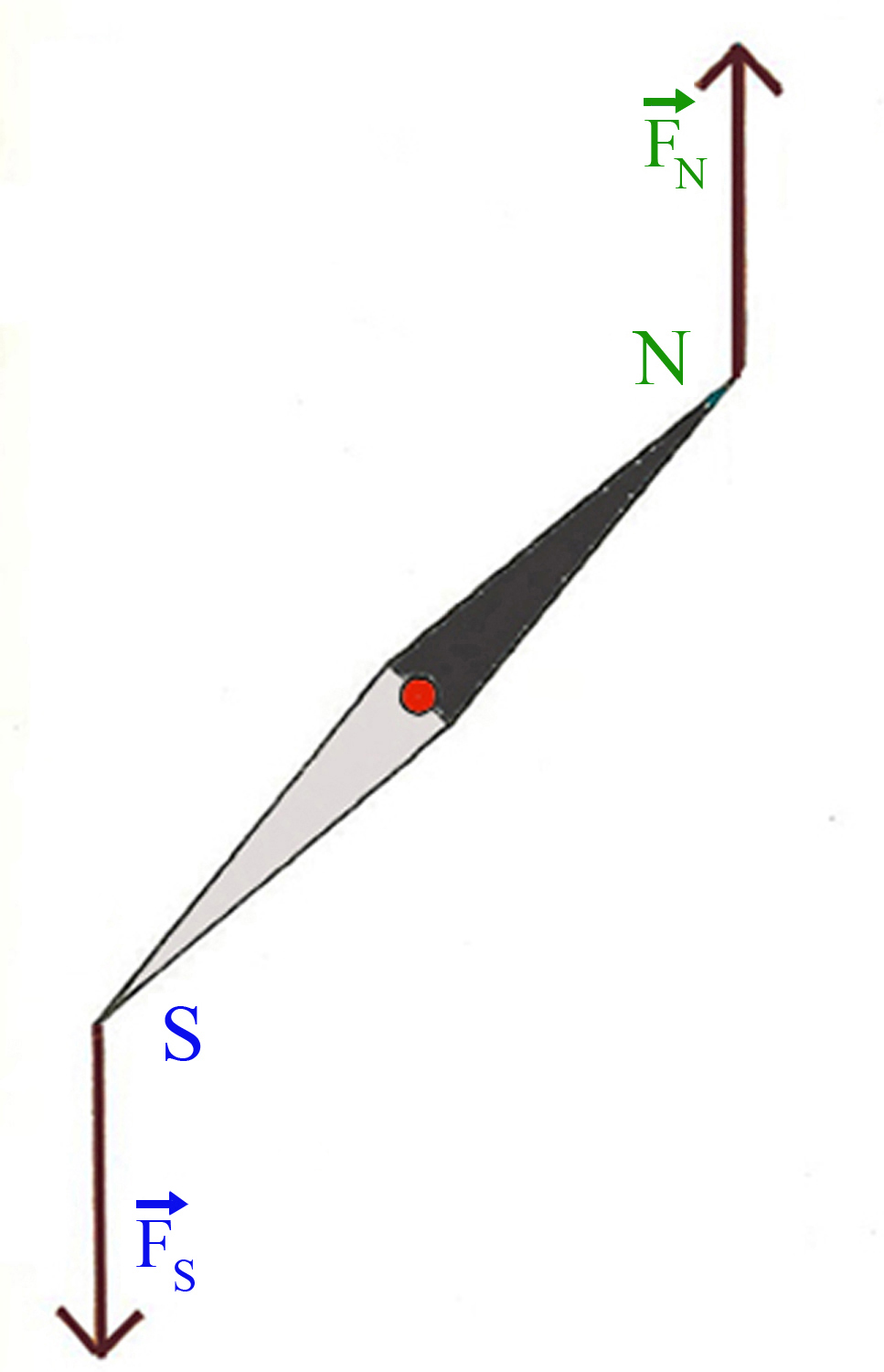
L`ago magnetico, quando si trova nella posizione di equilibrio, indica la direzione delle linee del campo magnetico in cui è immerso. È noto che se viene allontanato dall`equilibrio oscilla sotto l`influenza di una coppia di forze fino ad allinearsi.
Il rubino, che poggia sullo spillo del sostegno, assicura un basso attrito durante la rotazione e permette di ottenere l`allineamento al campo con buona affidabilità.
La magnetite e l`ambra si trovano ai primordi della storia del magnetismo e dell`elettricità.
Il Timeo di Platone parla di “pietra eraclea” descrivendo le proprietà magnetiche della pietra di magnesia, detta oggi magnetite (Fe₃ O₄). Questa era nota nell`antica Cina, i primi riferimenti molto incerti fanno risalire il suo impiego come bussola per scopi magici fin dall`83 d.C. (Lun Hêng di Wang Chung).
Sempre in Cina all`epoca Sung (960-1279) fu realizzata una bussola magnetica di cui esiste una descrizione dettagliata nel Wu Ching Tsung Yao di Tsêng Kung-Liang, un libro del 1084. Un pezzetto di ferro magnetizzato, inserito in un pesciolino di legno, era posto a galleggiare in una vaschetta colma d`acqua ad indicare il Sud.
La tradizione vuole che furono gli occidentali ad usare la calamita come bussola per la navigazione, verso la fine del XII secolo.
Secondo alcuni autori fu A. Necham nel 1180 a parlare dell`impiego degli aghi magnetici per l`orientamento, altri attribuiscono addirittura agli Olmechi la scoperta, risalente in questo caso a circa 3000 anni fa.
R. Norman, nato forse nel 1550, scoprì che l`ago magnetico, oltre ad orientarsi verso il nord, si inclinava rispetto al piano orizzontale. Per studiare questo comportamento progettò una bussola di inclinazione e pubblicò le sue osservazioni nel The Newe Attractive nel 1581 a Londra.
Uno studio del magnetismo terrestre, con un carattere di scientificità in senso moderno, è iniziato con la pubblicazione del De Magnete di W. Gilbert (1544-1603) avvenuta nel 1600. Egli costruì una terrella, cioè una sfera di magnetite naturale, e mostrò che un piccolo ago magnetico, posto in diversi punti della sua superficie, si comporta allo stesso modo dell`ago della bussola in vari luoghi della Terra.
La teoria moderna attualmente più accreditata si basa sui moti del nucleo fluido della Terra, ma le nostre conoscenze sul meccanismo che genera il campo sono ancora vaghe.   Fin dal secolo XVII sono state disegnate elaborate mappe dell`intensità e della direzione del campo magnetico riguardanti tutta la superficie della Terra.
In tempi più recenti, dall`esame delle rocce della crosta terrestre si sono ottenute informazioni che permettono di registrarne l`evoluzione nelle ere geologiche. Si sa quindi che il campo ha invertito la propria direzione all`incirca ogni milione di anni.
Gli aghi magnetici qui presentati sono costituiti di acciaio magnetizzato e, se posti lontani da campi magnetici artificiali o da oggetto ferromagnetici, si dispongono lungo il meridiano magnetico, che differisce da quello geografico; pertanto la parte che punta verso il Nord viene chiamata polo nord della calamita, mentre l`altra è il polo sud.
Attualmente tra il Polo Nord geografico e quello magnetico c`è una distanza di 1900 km.
 L`uso degli aghi magnetici ha permesso le prime scoperte sul magnetismo generato dalle correnti elettriche ad opera di H. C. Oersted nel 1820 che, secondo alcuni storici, fu preceduto dall`italiano G. D. Romagnosi fin dal 1802.   Seguirono poi molti altri: Biot e Savart, Ampere ecc.   Inoltre gli aghi magnetici hanno costituito i primi equipaggi mobili dei galvanometri e delle bussole dei seni e delle tangenti, come si può vedere anche in questo museo virtuale.
Bibliografia:
S. Weinberg, La scoperta delle particelle subatomiche, Zanichelli, Bologna 1986.
Enciclopedia della scienza e della tecnica, Vol. VI, Sadea Sansoni, Firenze 1965.
AA VV., The Project Physics Course, unità 4, Zanichelli, Bologna 1982.
R. Harré, Grandi esperimenti scientifici, Editori Riuniti, Roma 1983.
P. Caldirola, G. Casati e F. Tealdi, Fisica 2, Ghisetti e Corvi, Milano 1987.
C. R. Carrigan e D. Gubbins, La sorgente del campo magnetico terrestre, da Le Scienze n° 128 aprile 1979.
G. Goretti Miniati, Elementi di fisica, Vol. II, F. Cuggiani, Roma 1909.
L. Segalin, Fisica sperimentale, Vol. II, G. B. Paravia & C., Torino 1933.
O. Murani, Trattato elementare di fisica, Vol. II, U. Hoepli, Milano 1931.
R. Pitoni, Storia della fisica, STEN, Torino 1913.
F. Cajori, Storia della fisica elementare, Zanichelli, Bologna 1908.
B. Dessau, Manuale di fisica, Vol. III, S.E.L., Milano 1935.
Foto di Claudio Profumieri, elaborazioni, ricerche e testo di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.

 

 

 

 

 

 

 

 

Fischietto di Galton. Galton`s whistle. Sifflet de Galton.
Fabbricato dalla Leybold, matr. N° 798, non rinvenibile negli inventari, di data incerta.
Per maggiori informazioni cercare il tubo di vetro a filo di Kröncke della Leybold`s Nachfolger, che era un suo accessorio importantissimo, scrivendo: “Kröncke” su Cerca.
È usato come una sorgente di suono intenso e copre un range di frequenze da 6.000 a 30.000 Hz.
È calibrato ad un pressione di 1 atm ( 101.325 Pa) e sarebbe stato corredato da una scala di calibrazione che non è stata trovata.
Il fischietto è un tubo a flauto corto e chiuso. Il tubo ha un diametro di circa 4 mm ed è regolabile in lunghezza per mezzo di un pistone mobile comandato da una vite micrometrica.
L`orlo circolare frontale del tubo è sottile come la lama di un coltello, e viene soffiato attraverso un sottile beccuccio a forma di anello.
Il tubo e il beccuccio si trovano sullo stesso asse l`uno esattamente di fronte all`altro e sono fissati ciascuno su un braccio della forcella ad U.
La distanza fra di essi è tale da far ottenere il rendimento migliore.
Alla base della forcella è fissata una corta barretta di 10 mm di diametro per porre il fischietto su un sostegno.
L`aria compressa giunge attraverso il tubo metallico la cui estremità è a forma di oliva per fissarvi il tubo di gomma. Infatti normalmente il fischietto è alimentato da una pompa a motore; questo esemplare invece dispone di una pompetta oggi (2013) piuttosto malridotta.
I fischietti in uso nei primi del Novecento disponevano di una pompetta, come si vede nela figura tratta da: “A Catalogue of Physical Instruments Nr. 17 – L. E. Knott Apparatus Company, Boston, 1912”. Rinvenibile all’indirizzo:
https://ia802308.us.archive.org/34/items/catalogofphyinst00knotrich/catalogofphyinst00knotrich.pdf

Premesso che il suono acuto è molto direzionale, il fischietto di Galton è adatto per eseguire diversi esperimenti:
1) fa da sorgente sonora con gli specchi concavi (vedi sull’elenco, sezione Fisica: “Specchi ustori usati come riflettori acustici”);
2) generatore per la fiamma sensibile;
3) diffrazione di onde sonore;
4) sorgente per l`interferenza col tubo di Quincke;
5) vibratore per le lastre di Chladni; ecc. ecc.
  Francis Galton era un naturalista inglese (1822 – 1911).
Bibliografia: Scheda istruzioni N° 41270/41273 della E. Leybold`s Nachfolger – Köln – Bayental 8/1964 A, che riportiamo.
Foto di Claudio Profumieri, elaborazioni, ricerche e testo di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.

 

 

 

 

Spettrometro Monocromatore modello M.G.1.
L`inventario D del 1937 in data 7 novembre 1955, riporta l`acquisto di uno “Spettrometro modello N completo” costruito dalle Officine Galileo – Firenze. Il numero di matricola è O61a 00117.
Riportiamo integralmente la scheda L 924 delle Officine Galileo Firenze, tratta da: Spettrometro Modello “N” e Monocromatore – L 923 – 924 ediz. 1938 e 1950.
«Per trasformare lo spettrometro precedente in un ottimo monocromatore basta togliere l`oculare di osservazione e sostituirlo con una seconda fenditura disposta nel piano ove si forma l`immagine dello spettro. La rotazione del prisma porta le successive righe dello spettro in corrispondenza della seconda fenditura, e da questa esce un fascio di raggi monocromatici. Se la sorgente fornisce uno spettro a righe ben separate (arco a vapore di sodio, cadmio, ecc), l’apparecchio dà luce veramente monocromatica; se invece produce uno spettro continuo, il fascio emergente comprende una ristretta regione dello spettro, che varia con continuità ed è tanto meno estesa quanto più sottili sono le due fenditure. Il secondo caso si verifica quando si usa la fenditura con edicola [come nelle foto N.d.R.], perché l’edicola contiene una lampada ad incandescenza in funzione di sorgente. Detta lampada è completa di condensatore e trasformatore universale di alimentazione. Lunghezza d`onda delle radiazioni più comuni:
Fiamma al sodio: 2 righe gialle vicinissime, 5890 A. 5896 A.
Arco a mercurio 1 ruga verde (oltre il resto) 5461 A.
Tubo di Plücker a elio 1 riga gialla (oltre il resto) 5876 A».
  Una spiegazione più lunga è riportata nelle Istruzioni “MONOCROMATORE – SPETTROMETRO M.G.1”. (dove è scritto: “Dimensioni cm 40×50×85 – Peso: Kg 15,400”)
In esse viene descritta la taratura usando ad esempio “una semplice fiamma al sodio o una lampada ad arco nei vapori di sodio” posta davanti alla fenditura moderatamente allargata, sulla quale in seguito si dovrà montare la lampada ad incandescenza a filamento concentrato in dotazione. Si ruota poi il tamburo fino a quando sulla graduazione non si legge il valore della lunghezza d’onda relativa al doppietto del sodio (589 – 589,6 nm) che, a causa del fascio allargato è di 589,3 nm. Poi si diminuisce la larghezza delle fenditure di ingresso e di uscita fino ad ottenere la massima luminosità. Ecc.
Nella prima foto si vedono montate sia la seconda fenditura sia l’edicola, mentre l’oculare di osservazione per l’uso come Spettrometro è posato sul tavolo. Nella quarta foto si vedono affiancate: la seconda fenditura per l’uso come monocromatore e l’edicola per l’uso come monocromatore in luce bianca.
Oggi siamo abituati all’uso del laser, ma prima del suo avvento era necessario ricorrere al monocromatore quando si volevano eseguire esperimenti con luce monocromatica.


La figura 1 del monocromatore è a pag. 3 e la figura 2 dello spettrometro è a pag. 4 delle Istruzioni: Monocromatore – Spettrometro M.G.1 delle Officine Galileo.  Nella figura 1, C₁ e C₂ sono i due collimatori per il montaggio come monocromatore. Nella figura 2 C₁ è il collimatore di entrata e C₃ è un cannocchiale astronomico con reticolo a croce in funzione di collettore, per l’uso come spettrometro. Questi due strumenti sono dunque intercambiabili, presentano richiami a nasello per il bloccaggio e sono muniti di obiettivi “trattati” aventi: Ø = 21 mm, f = 204 mm, apertura relativa 1 : 9. In corrispondenza dei piani focali degli obiettivi dei collimatori C₁ e C₂ sono sistemate le due fenditure F₁ e F₂. La loro grandezza è regolabile mediante viti micrometriche (che spostano simmetricamente entrambi i lembi delle fenditure) ed è misurabile con una approssimazione di 0,01 mm su apposito tamburo graduato.
Come primo caso si consideri una sorgente eterocromatica come ad esempio la luce di una lampadina.
Un fascio di questa luce, che incida sotto un dato angolo sulla faccia di entrata del prisma, viene disperso producendo sul piano della fenditura di uscita F₂ una immagine di F₁. Per ciascun valore dell’angolo di incidenza sulla prima faccia del prisma si ottiene quindi all’uscita dello strumento un unico pennello luminoso avente “una ristretta regione” intorno ad una determinata lunghezza d’onda λ.

Nel secondo caso (vedi la figura 8 tratta da NOTIZIE PER I LABORATORI SCIENTIFICI E INDUSTRIALI A CURA DELLE OFFICINE GALILEO – FIRENZE N° 73 Luglio 1933 SPETTROSCOPI / SPETTROGRAFI Spettroscopio modello piccolo) si ha la presenza di una edicola con condensatore ottico insieme ad un trasformatore universale che alimenta una lampadina a filamento concentrato. L’edicola è provvista di due regolazioni: una longitudinale per focheggiare l’immagine del filamento sul piano della fenditura F₁, una trasversale per centrare l’immagine. dalla fenditura F₂ del collimatore C₂ esce allora un pennello di luce cromatica, la cui lunghezza d’onda è leggibile sul tamburo. Tralasciamo comunque la lunga descrizione della taratura e della messa a punto dello strumento.
La tabella qui sotto chiude le Istruzioni.

La figura L 924 del modello tipo N si trova a pag. 214 del catalogo: Apparecchi per l’Insegnamento della Fisica a cura del prof. R. Magini, Officine Galileo, 1940.

Se si desidera consultare la scheda riguardante lo Spettrometro M.G.1, si può scrivere “M.G.1” su Cerca.
Foto di Claudio Profumieri, elaborazioni, ricerche e testo a cura di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.

 

 

 

 

 

Amplificatore in B.F. e altoparlante PHYWE.
L`amplificatore del tipo PHYWE BF 07550.93, acquistato per questo apparato a microonde nel 1966, è piuttosto sofisticato in quanto funziona sia come normale amplificatore in bassa frequenza, sia come amplificatore di misura.
In entrambi gli usi, il guadagno resta praticamente costante (entro circa 3 dB) per le differenti gamme di frequenze.
Nel disegno si evidenziano: 1) Interruttore; 2) Lampadina spia d`accensione: 3) Ingresso segnale; 4) Uscita amplificatore di misura; 5) Uscita 5 kΩ amplificatore bassa frequenza; 6) Uscita 4 Ω amplificatore b. f.; 7) Tasti per la scelta del modo di funzionamento e il rilevamento dei bassi e degli acuti; 8) Tasti per la regolazione grossolana del guadagno; 9) Potenziometro lineare a quadrante per la regolazione fine del guadagno; 10) Prese per l`alimentazione di cellule fotoelettriche e di fotodiodi; 11) Indicatore di sovramodulazione; 12) Presa per messa a terra.
L`apparecchio permette sia l`alimentazione sia l`amplificazione di correnti fornite da cellule fotoelettriche o fotodiodi.
Nel suo funzionamento come amplificatore in b.f., la potenza di uscita è sensibilmente più elevata che non in quella come amplificatore di misura. In quest`ultima funzione il guadagno va da 0 fino a 104, valori validi per una resistenza di uscita R<sub>u</sub> = 10 kΩ. Se ad esempio si sceglie il tasto 102 e il potenziometro si trova sul 0,6, significa che si ha un guadagno di 60.
Senza entrare in ulteriori dettagli riportati nelle schede di istruzione consultate, si danno qui alcune specifiche tecniche nel suo uso come amplificatore di b.f.: Impedenza di ingresso 1 MΩ; Gamma di frequenze da 100 Hz a 16 kHz senza rilevazione, da 40 Hz a 25 kHz con rilevazione (sempre entro 3 dB); Tensione d`uscita max. 3,7 V ( R_ext = 4 Ω ), V max 120 V (R_ext = 5 kΩ); Potenza d`uscita max 35 W; Distorsione circa 5%.
Nell`uso come amplificatore di misura: Impedenza di ingresso 1 MΩ; Gamma di frequenza da 15 Hz a 80 kHz (entro 3 dB); Tensione di uscita max. 20 V (R_ext = 10 kΩ); Resistenza interna 350 Ω; Distorsione 2%.
L`altoparlante elettrodinamico a magnete permanente e impedenza della bobina mobile di 4 Ω della PHYWE ha al suo interno un trasformatore d`adattamento per 7 kΩ. Bibliografia.
Scheda di Istruzioni della Phywe A.G. Göttingen, N° 07550.93 senza data, da cui è tratta la figura.
Per consultare due delle 4 schede  scrivere “microonde” su Cerca; per vedere l`altra scheda scrivere “Klystron” su Cerca.
Foto di Federico Balilli, elaborazioni, ricerche e testo di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.

 

 

 

 

                                 Biprisma di Fresnel.
  Nell`appendice dell`inventario del 1937 risulta registrato in data 23 dicembre 1955 e al n° 1690 si legge: “Biprisma di Fresnel ₤ 26.200”.
Nell`inventario D del 1956 al n° 888 si legge: “Biprisma di Fresnel” destinato a Fisica.
  Negli anni 1818 – 1819, A. J. G. Fresnel (1788 – 1827), non essendo soddisfatto di ottenere la figura di interferenza della luce per mezzo di due fenditure, ideò e costruì due dispositivi: gli specchi di Fresnel (un esemplare di questi si può osservare in questo sito) e il biprisma.
  Per ottenere interferenza con le due fenditure sia T. Young nel 1803 che successivamente Fresnel collimavano un fascio di luce monocromatica per poi inviarlo su due fenditure sottili e vicine.
Ma l`interferenza così ottenuta è modulata dalla doppia diffrazione dovuta alle due fenditure.
Invece il sistema dei due specchi o il biprisma permettono di ottenere interferenza pura trasformando un raggio di luce monocromatica in due raggi, come se provenissero da due sorgenti distinte “in fase” tra loro.
Il biprisma in realtà è un solo prisma a sezione triangolare isoscele con l`angolo al vertice di poco inferiore ai 180°; nelle figure sottostanti esso è accentuato per esigenze didattiche.
Il nome deriva dal fatto che idealmente sarebbe formato da due prismi rettangolari uniti per il cateto minore.
 Da quando in laboratorio si dispone della luce laser il suo uso si è molto semplificato: è sufficiente allargare il fascio laser, con una lente di ottima qualità o meglio con l`oculare di un microscopio, e dirigere la luce sul vertice del biprisma, perpendicolarmente alla sua base, per avere belle frange di interferenza di intensità abbastanza uniforme, visibili su uno schermo posto a distanza opportuna.

Nella figura 4 la zona di interferenza è rappresentata dal triangolo scuro.
Normalmente la prima spiegazione di questo fenomeno che si fornisce nelle scuole si basa sulla teoria ondulatoria.
Recentemente il prisma di Fresnel è tornato in auge per alcuni esperimenti molto sofisticati che non si possono spiegare col modello ondulatorio ma che richiedono una moderna teoria detta elettrodinamica quantistica.
La teoria ondulatoria, che spiega l`interferenza, richiede che onde elettromagnetiche monocromatiche e inizialmente in fase tra loro si influenzino reciprocamente, dando luogo sullo schermo a zone di interferenza costruttiva e distruttiva, in ragione dei reciproci percorsi in uno spazio isotropo.
Una tale teoria non è in grado di spiegare cosa accadrebbe se si mandassero fotoni uno alla volta su un biprisma o verso le due fenditure.
La domanda cruciale in tal caso è: “Con cosa interferisce un singolo fotone?”.
Il primo esperimento in tal senso risale a G. I. Taylor, che nel 1908 cercò di inviare della luce monocromatica estremamente debole su due fenditure; il risultato fu insoddisfacente.
R. P. Feynman nel 1964 rilanciò l`idea descrivendo un esperimento ideale; ma già c`erano stati tentativi sperimentali di questo tipo.
Nel 1973 P. Merli, G. F. Missiroli; e G. Pozzi a Bologna realizzarono “l`esperimento più bello della fisica”: interferenza di elettroni uno alla volta con un biprisma formato da campi elettrostatici.

Nel 2005, un folto gruppo di ricercatori, i cui nomi sono riportati nella bibliografia, ha finalmente realizzato interferenza di un fotone alla volta con un biprisma e tecniche molto sofisticate. Il risultato è visibile nella seconda figura qui sotto: fino ad un numero di 272 fotoni sullo “schermo” si vedono puntini ben distinti e sparsi senza alcun disegno apparente; raggiunto il numero di 2240 fotoni si cominciano a delineare le frange; con 19773 fotoni le frange sono nette.
Non è questa la sede per spiegare il significato teorico dei due ultimi esperimenti accennati; essi bastano comunque per porsi una domanda ingenua: “Come fa ogni fotone a sapere ciò che hanno fatto quelli che lo hanno preceduto e ciò che faranno i successivi per decidere dove colpire lo schermo?”.
L`elettrodinamica quantistica, col suo modo bizzarro e lontano dal senso comune, lo spiega con le sue particolari leggi probabilistiche.
Per quanto nessuno, credo, si senta soddisfatto dalla strana descrizione di come vanno le cose.

Bibliografia.
V. Ronchi, Storia della Luce, Laterza, Bari 1983.
R. P. Feynman, La legge fisica, Boringhieri, Torino 1971.
P. Merli, G. F. Missiroli; e G. Pozzi, Diffrazione ed Interferenza di elettroni; Giornale di Fisica, Bologna Luglio-Settembre 1974.
G. Giuliani, Interferenza, Giornale di Fisica, Bologna Gennaio-Marzo 2007.
C. Giacomarra, Luce e Materia, Onde e Particelle: un possibile percorso didattico attraverso i fenomeni di interferenza, Giornale di Fisica, Bologna Aprile-Giugno 2009, da cui è tratta la  figura 4.
V. Jacques, E. Wu, T. Toury, F Treussart, A. Aspect, P. Grangier, J. F. Roch, Single-photon wavefront-splitting interference, The European Phisical Journal D, 2005, da cui sono tratte le altre figure.
Foto di Claudio Profumieri, elaborazioni, ricerche e testo di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.