Categoria: fisica

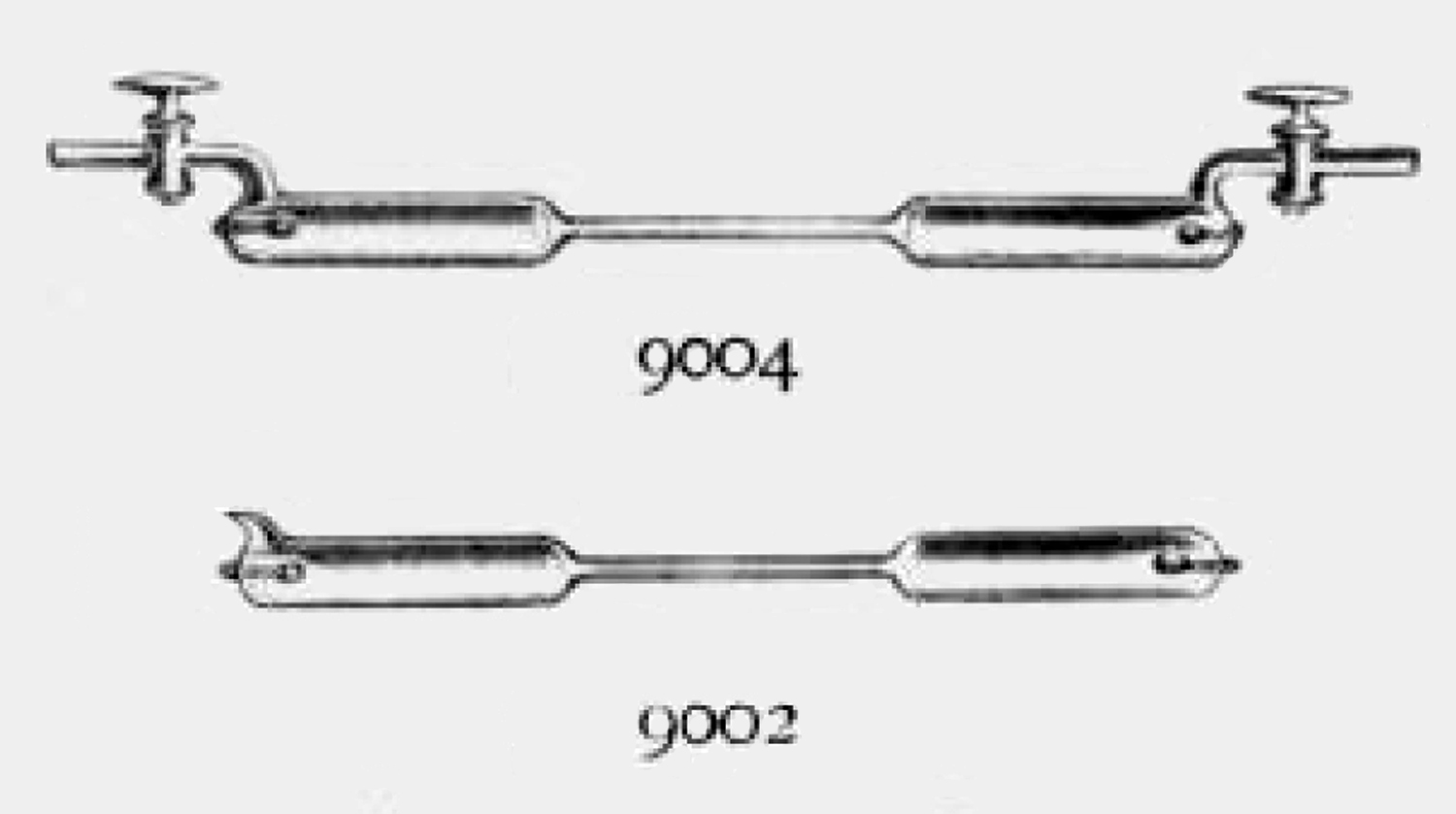
  Apparecchio per mostrare il principio di Pascal.
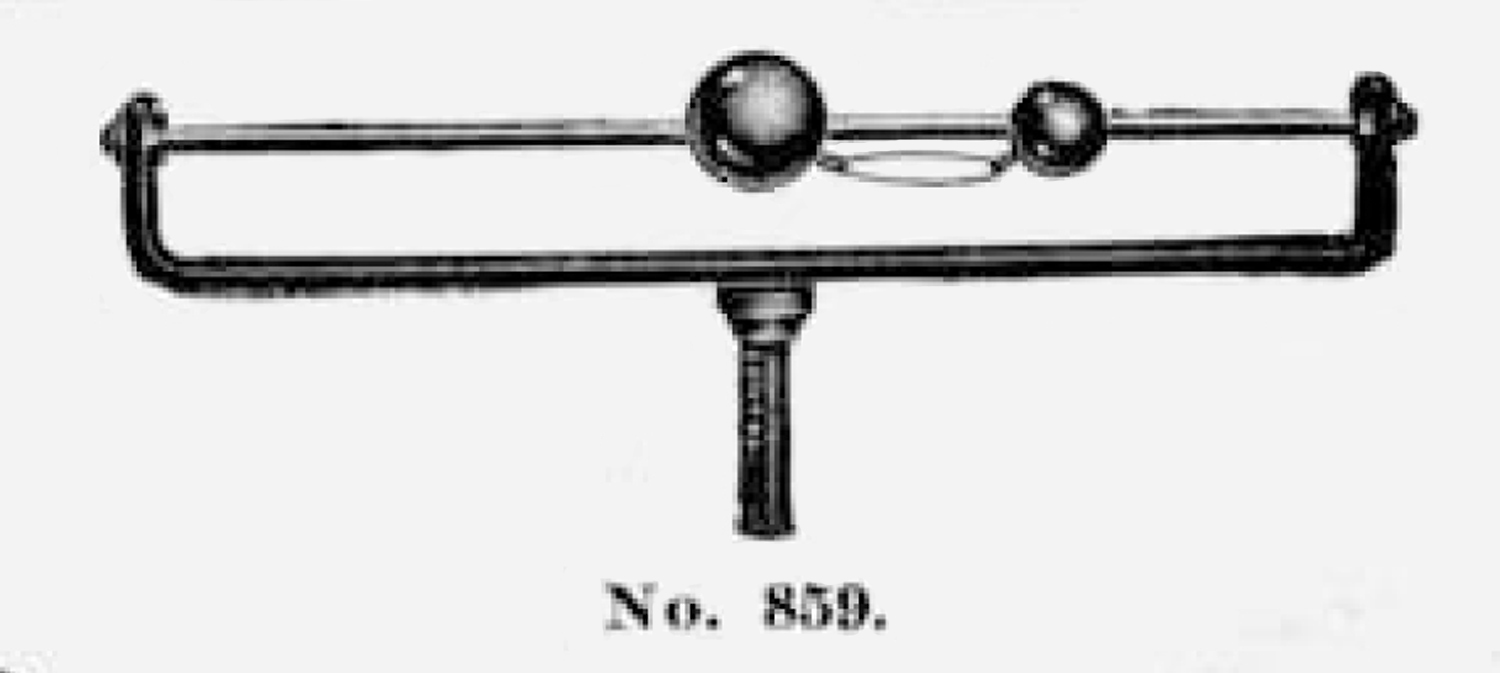
Nell’inventario del 1912, pag. 50 n° 862, si legge: “Sfera di vetro munita di un tubo con stantuffo per dimostrare che la pressione si comunica egualmente in tutte le direzioni. Condizione: rotta; ₤ 1”.
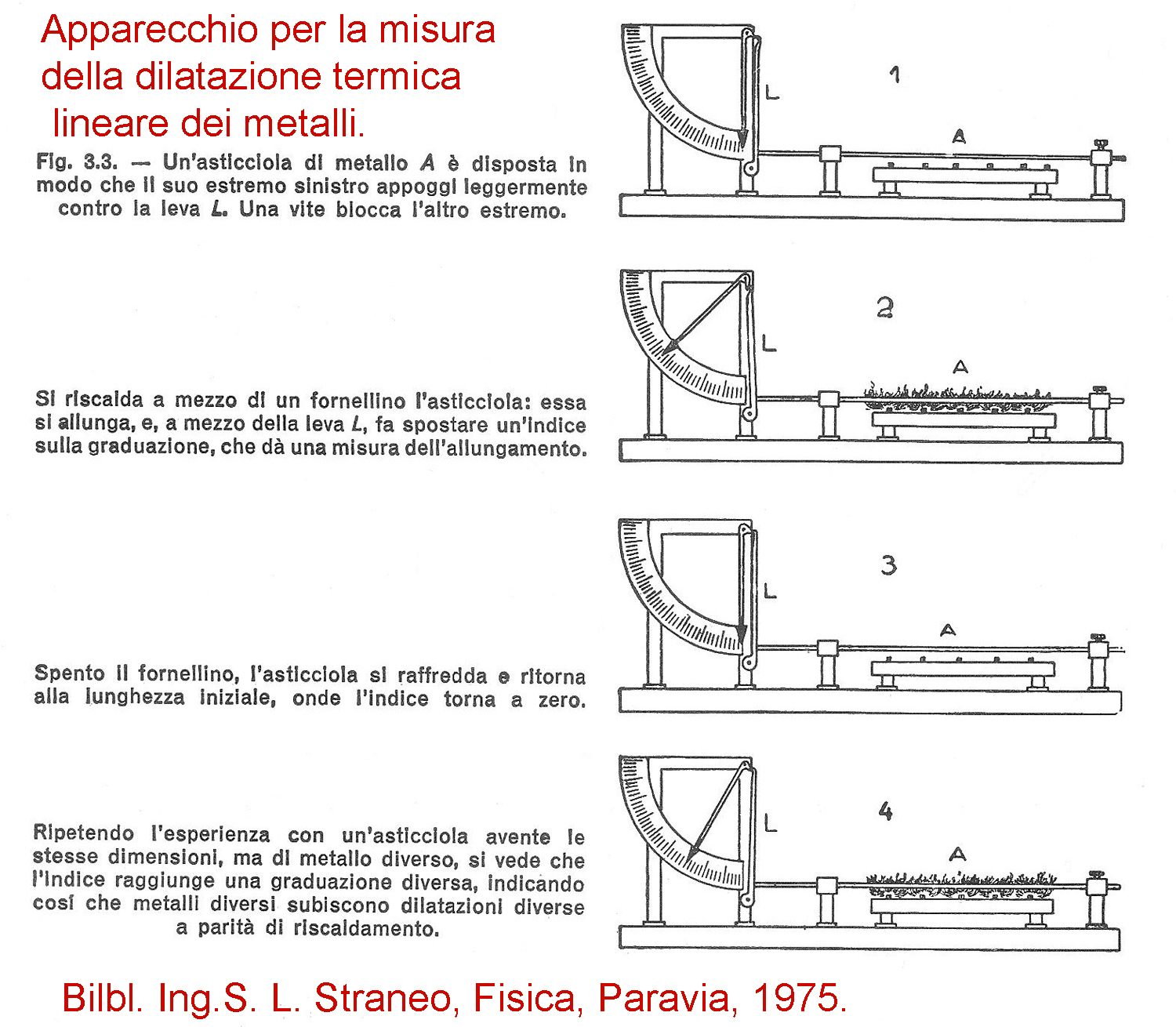
Esso serve per mostrare che la pressione esercitata su una porzione di in un fluido si manifesta in tutte le direzioni con la stessa intensità.
L’ing. Claudio Profumieri ha sottoposto questo esemplare ad un lievissimo ed efficace restauro non invasivo nell’ottobre del 2013.
 Il principio di Pascal prende il nome dal francese Blaise Pascal (1623-1662), che lo enunciò alla metà del Seicento.
È bene sottolineare che questo fenomeno non è intuitivo: lo spettatore ignaro tende a pensare istintivamente che la pressione sia maggiore nella direzione del moto dello stantuffo.

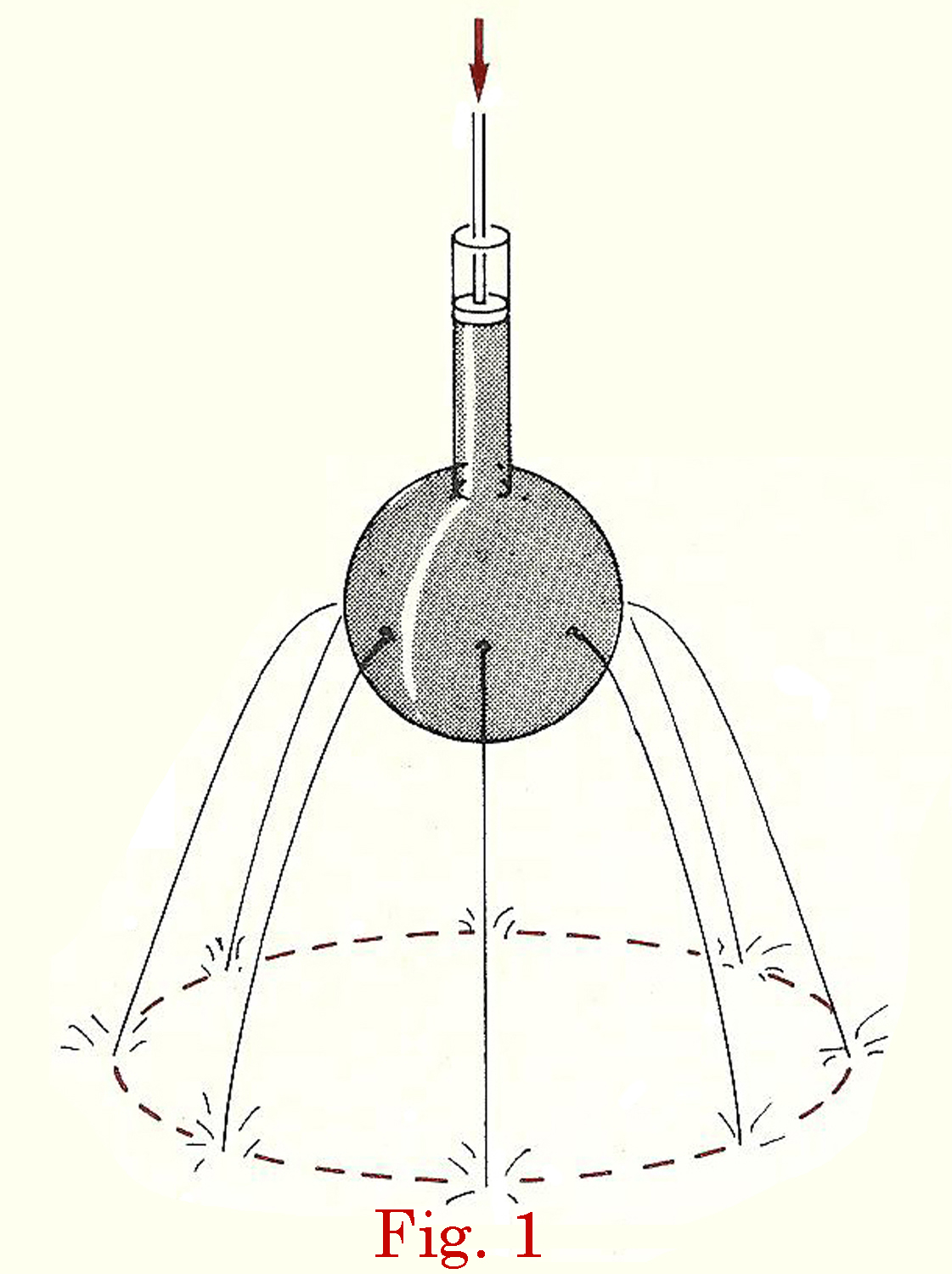
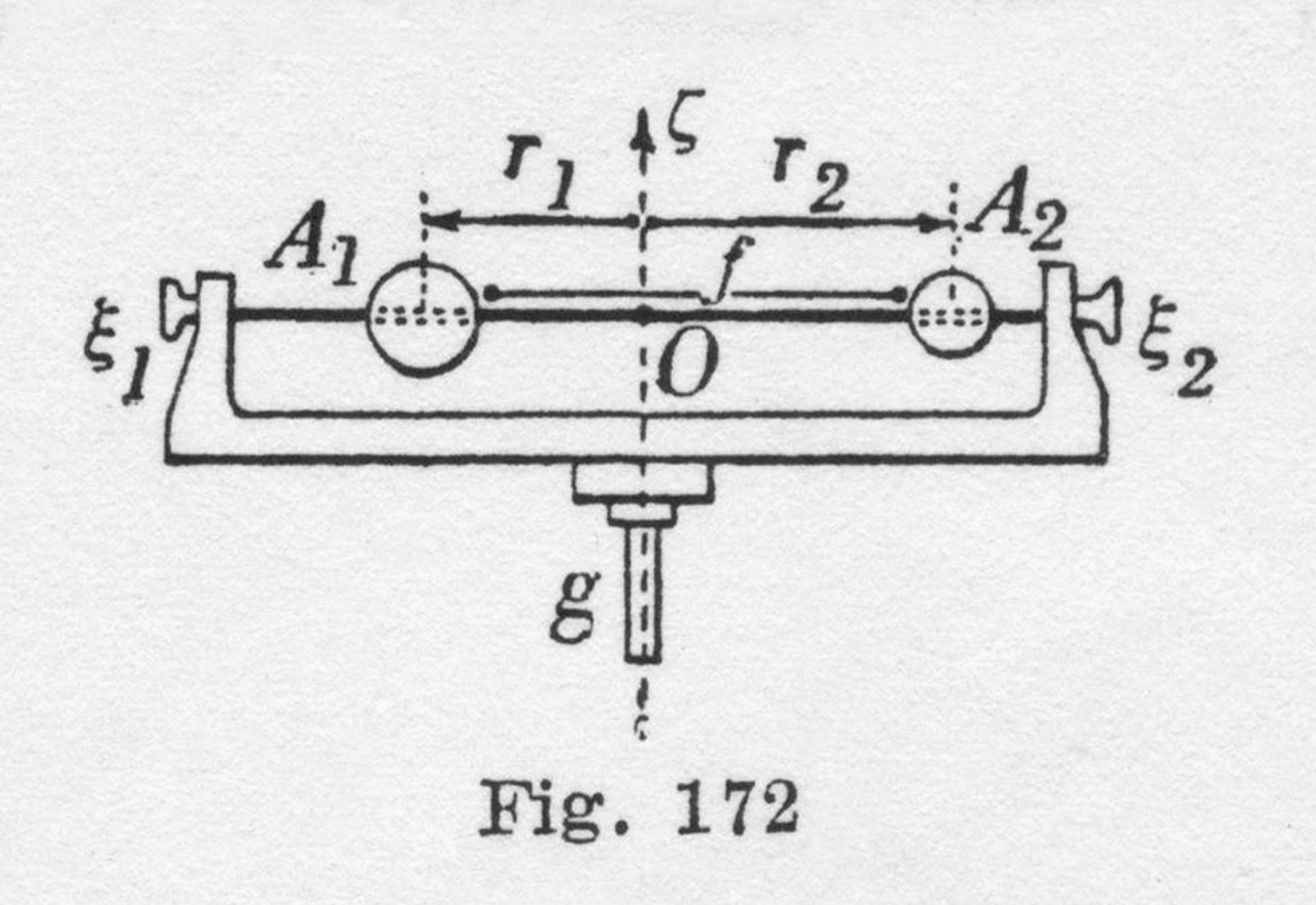
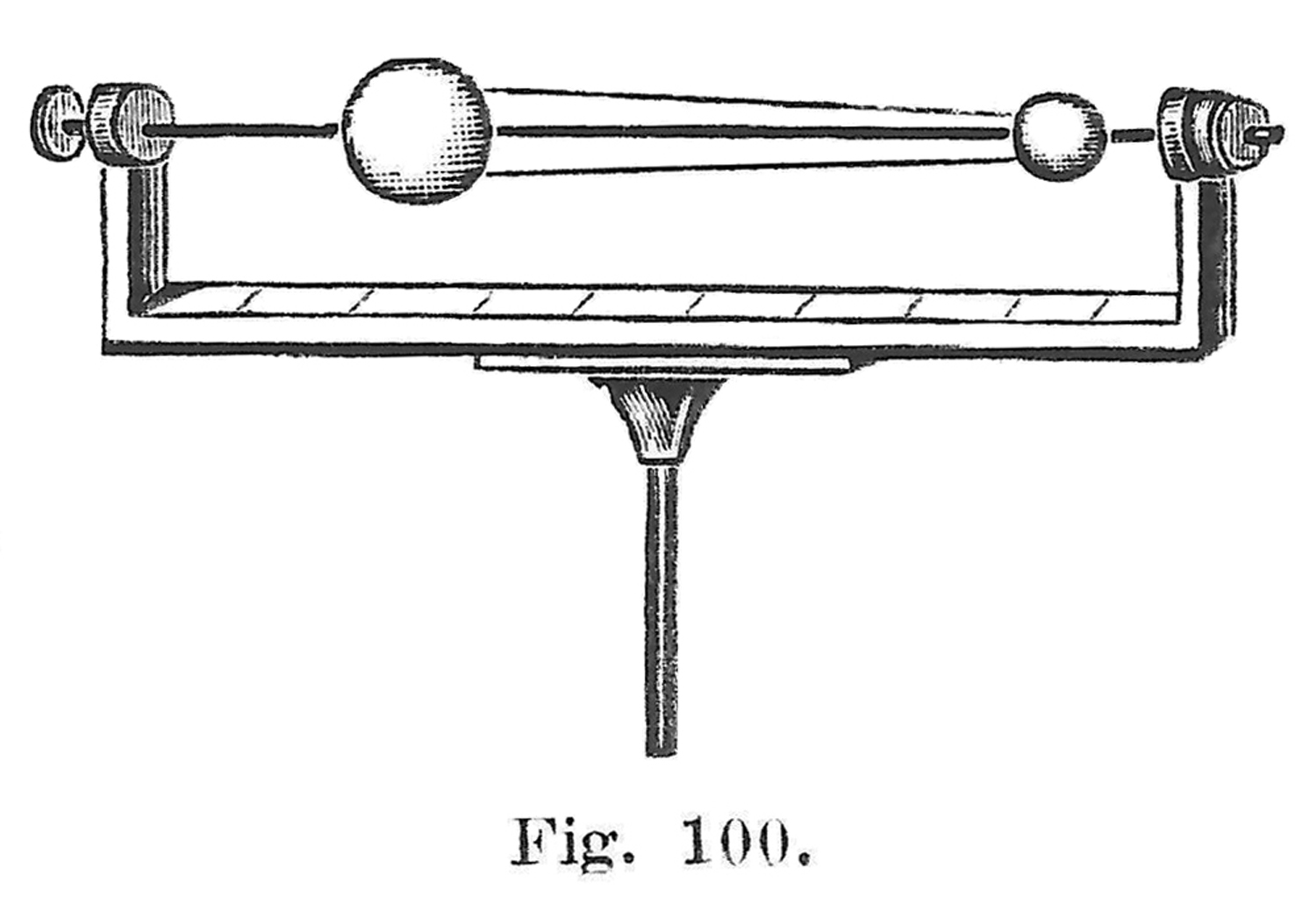
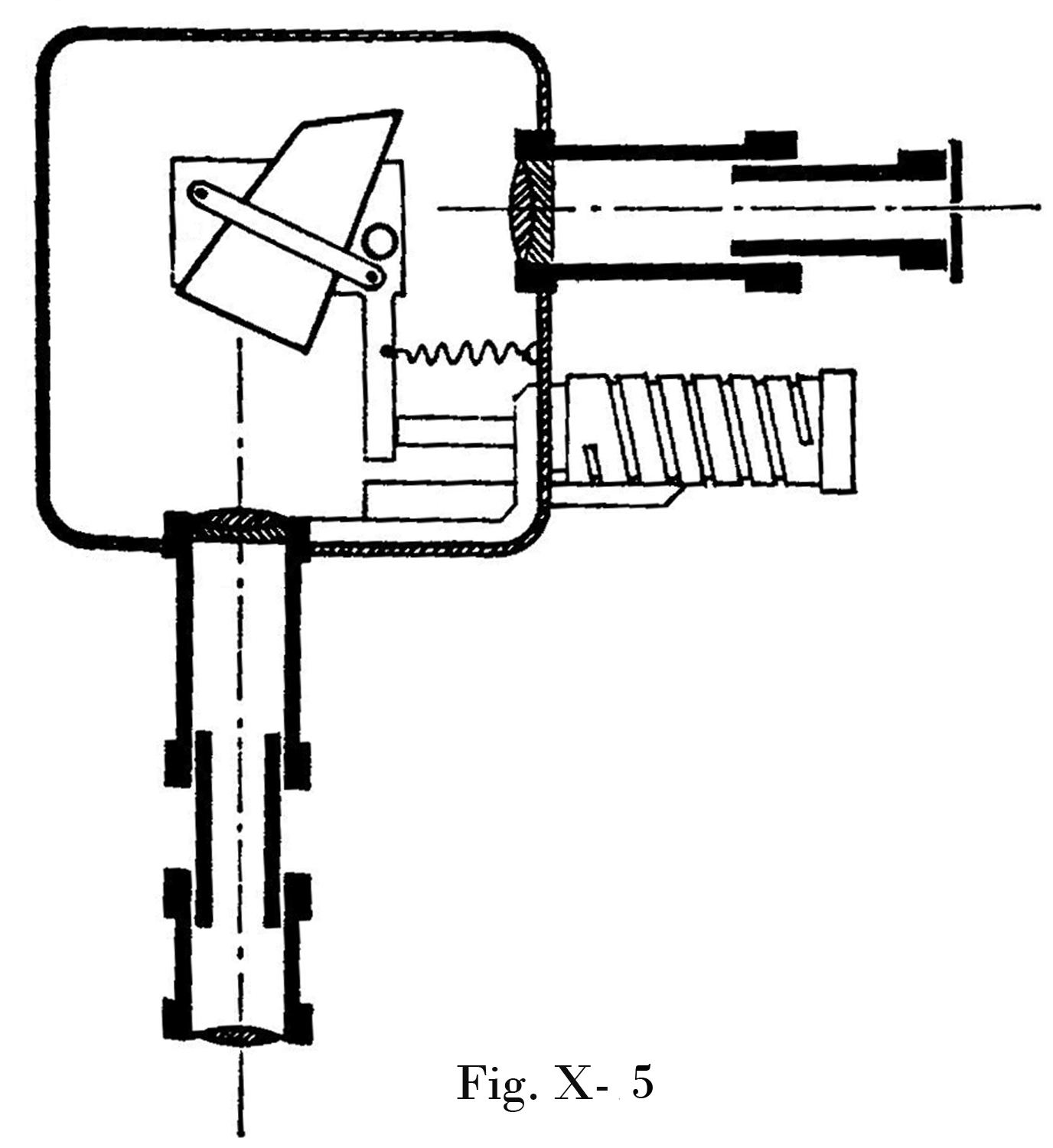
L’oggetto è costituito da un cilindro di vetro nel quale scorre uno stantuffo; il cilindro si allarga in un`ampolla con dei fori ai quali si adattano bene i turaccioli forati nei quali si infila una estremità di ogni tubicino ad U.
Detti tubicini funzionano da manometri.
Vi sono ben tre modi diversi per eseguire la dimostrazione: 1) si mette dell’acqua colorata nei tubicini fino a che nel ramo vicino al turacciolo arrivi sotto il gomito, mentre l’ampolla contiene aria, si agisce sul pistone e si osserva l’acqua salire nel ramo libero di ogni tubicino assumendo lo stesso dislivello, 2) si riempie l’ampolla con acqua, preferibilmente colorata, in modo tale che essa raggiunga un certo livello nei tubicini ad U, osservando solo che il liquido sale della stessa entità in ogni tubicino; 3) si mette del mercurio nei tubicini con la stessa modalità eseguita al punto 1), e poi si riempie l’ampolla con acqua colorata; in questo caso il mercurio richiede una pressione maggiore sullo stantuffo per ottenere lo stesso aumento del livello, poiché il mercurio ha una densità 13,546 volte maggiore dell`acqua.
L’uso del mercurio (o dell’acqua colorata nel primo caso) permette di calcolare la pressione esercitata sullo stantuffo, misurando il dislivello tra il pelo libero del mercurio nel ramo aperto e la superficie di separazione mercurio-acqua nell’altro ramo, con la legge di Stevin p = d g h dove d è la densità del mercurio (o dell’acqua), g è l’accelerazione di gravità e h è il dislivello, mantenendo lo stantuffo nella posizione finale.
Si tenga conto che il livello del liquido nel ramo aperto deve equilibrare anche la pressione dovuta al peso dello stantuffo e quella esercitata dalla colonna di liquido nel tubo. Ecco dunque che usando l’acqua (o l’aria nel primo caso) è bene tenere lo stantuffo con una mano per evitare che il suo solo peso faccia defluire l’acqua; mentre il mercurio è idoneo a mantenerlo fermo. Nel fare queste ultime considerazioni bisogna tenere anche conto dell`attrito dello stantuffo con il tubo.
Una variante di questo apparecchio consiste in un’ampolla dotata di fori disposti lungo una sua circonferenza e si fa vedere semplicemente che, posta la circonferenza orizzontalmente e spinto lo stantuffo, l’acqua zampilla dai fori disegnando un cerchio sul pavimento.

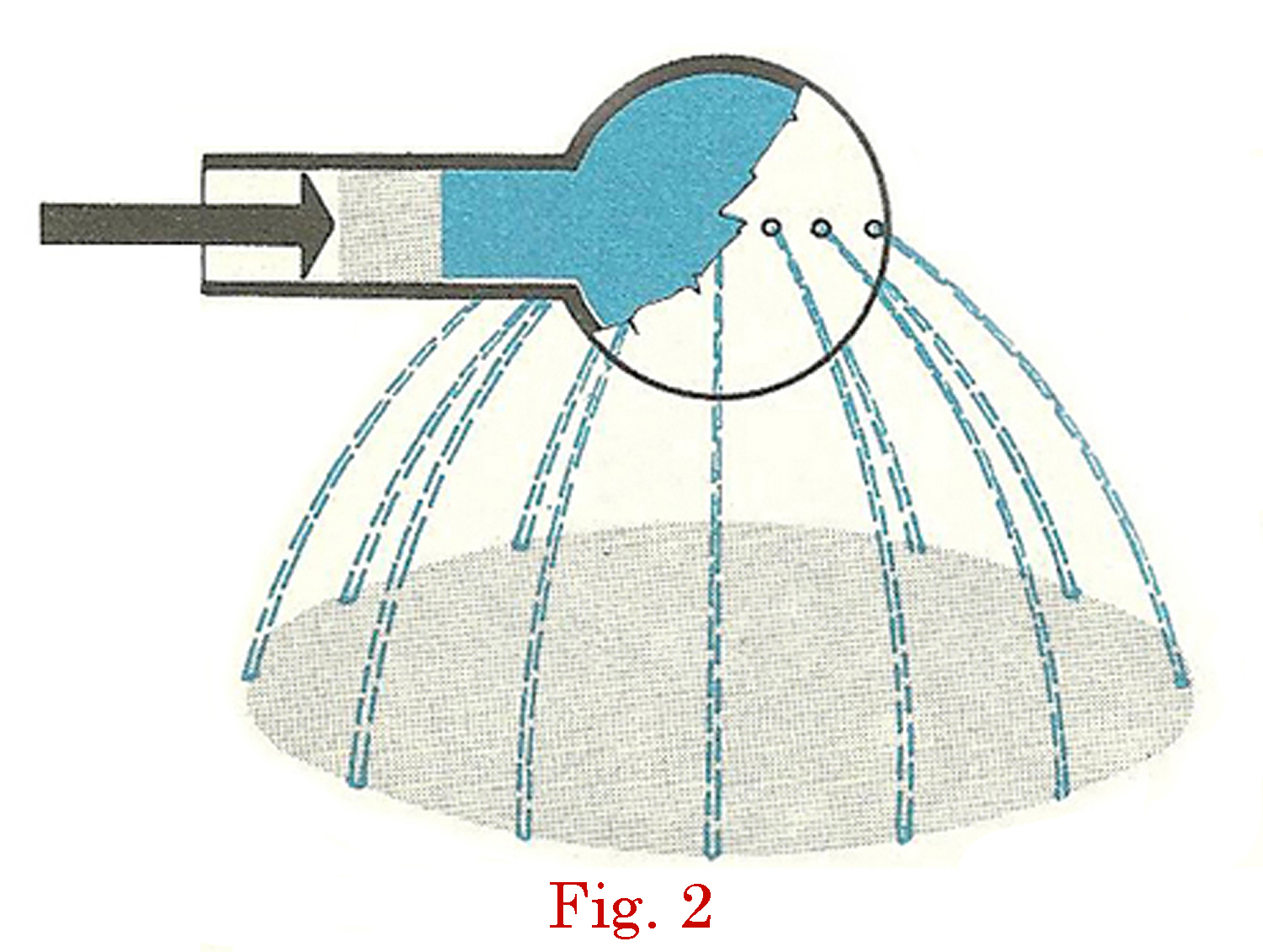
Però questa dimostrazione richiede che gli allievi sappiano che la stessa pressione provoca la stessa velocità di efflusso con la stessa energia potenziale (per il noto teorema di Bernoulli sulla conservazione dell`energia per i liquidi ideali in moto stazionario) e che, a parità di velocità iniziale orizzontale, si ha la stessa gittata.
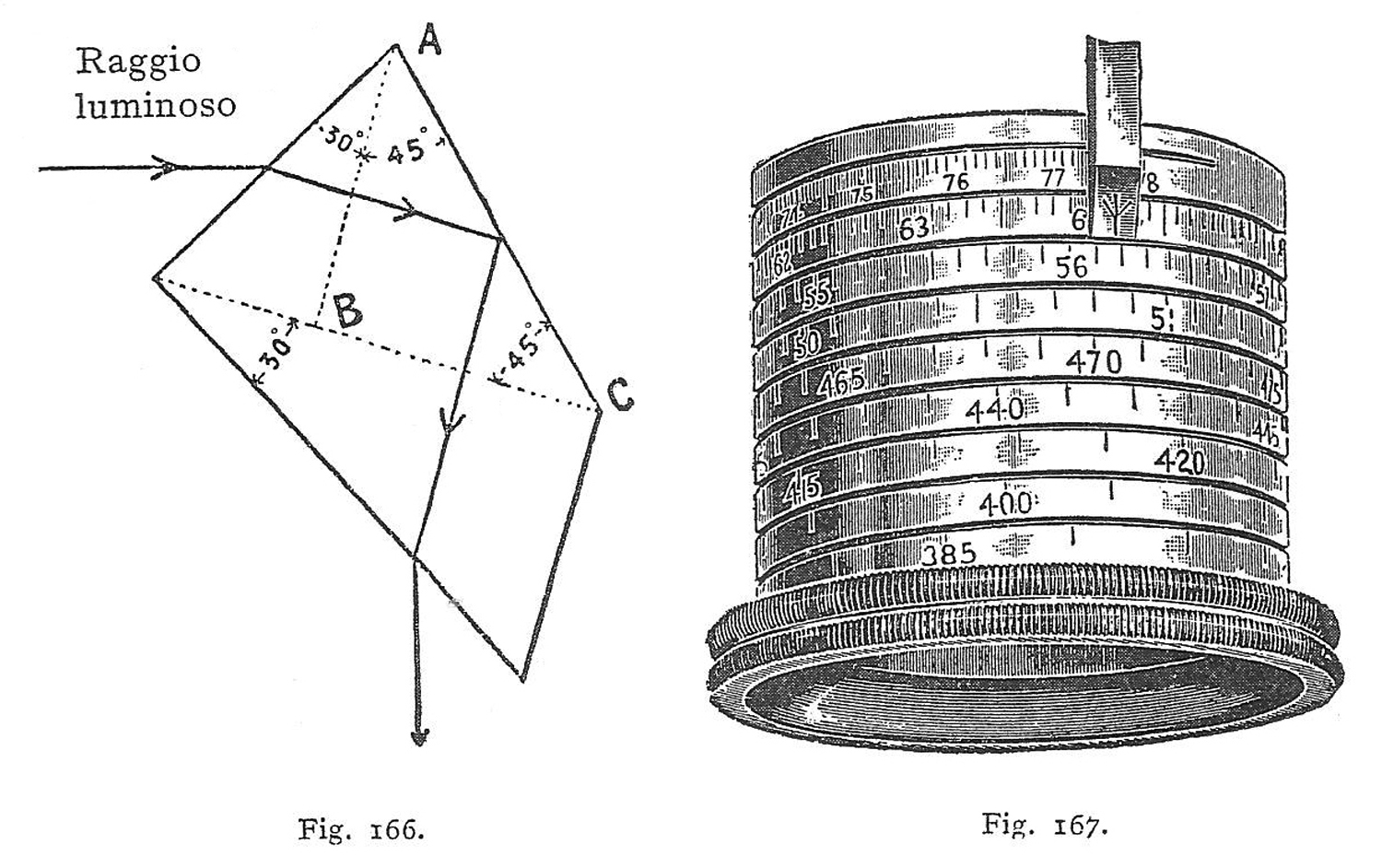
La figura 688 è a pag. 32 del Catalogue of Physical Apparatus (With descriptions and instructions for use) E. Leybold’s Nachfolger Cologne [1910?], rinvenibile all’indirizzo:
https://www.sil.si.edu/DigitalCollections/trade-literature/scientific-instruments/files/52546/
Bibliografia.
P. Calvani e B. Maraviglia, Introduzione alla Fisica, Vol. A, Laterza, Bari 1977da cui è tratta la figura 1.
S. Donati, Nozioni di Fisica, S. Lattes & C., Torino 1972 da cui è tratta la  figura 2.
M. Fazio e M. C. Montano, Una Fisica Nuova, Vol. I, Morano, Napoli, 1984.
  Foto di Claudio Profumieri, elaborazioni ricerche e testo di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.

 

 

 

Apparecchio per la misura della dilatazione termica lineare.
Nell`inventario del 1906, n° 825, è detto già esistente. Si stima di fine Ottocento.
Costruttore Lana ’a Turin.

  Era utile per mostrare l`aumento della lunghezza della sbarretta di metallo quando veniva riscaldata alla fiamma. Come combustibile si usava l`alcol, posto nel serbatoio dove pescano gli stoppini.
È interessante il meccanismo che amplifica e visualizza la dilatazione.

Il serbatoio con gli stoppini può ruotare sui cardini per facilitare la carica dell’ alcol.

Si potevano fare confronti qualitativi sulla diversa dilatazione, avendo a disposizione una serie di sbarrette simili, costituite da vari metalli.
  Una spiegazione, seppure molto approssimativa, della dilatazione dei solidi è la seguente.
L`energia ricevuta, fa muovere più velocemente gli atomi che, per urto, comunicano a quelli vicini una energia cinetica che ne aumenta la vibrazione. Questo li fa allontanare di più dal loro centro di vibrazione,
opponendosi così alle forze che tengono legati tutti i solidi. L`energia si propaga, per urti successivi tra atomi, a tutto il solido, pertanto, pur non rompendo questi legami, le distanze interatomiche aumentano. Tutto ciò è dovuto ad una asimmetria della curva dell`energia potenziale in funzione della distanza internucleare: la distanza media aumenta all`aumentare della temperatura e quindi dell`energia vibrazionale.

Bibliografia.
D. Halliday e R. Resnick, Fisica, vol. I, C.E.A. Milano 1982.
Ringrazio il Prof. Roberto Mantovani dell`Università di Urbino per avermi segnalato il nome del costruttore che è  leggibile sul quadrante.
L’apparecchio è esposto al Museo MITI, su proposta di Fabio Panfili.
   Foto di Daniele Maiani e di Claudio Profumieri, elaborazioni, ricerche e testo di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.

 

 

 

 

 

 

 

 

 

 

 

 

 

Apparecchio di Tyndall. Casa costruttrice Max Kohl A. G. – Chemnitz.
John Tyndall [1820-1893], fisico nato in Irlanda ma trasferitosi in giovane età in Inghilterra.
Nell’inventario del 1912 si trova al n° 873 di pag. 51. Vi si legge: «Apparato di Tyndall per dimostrare la dilatazione per il calore e la contrazione per il freddo con la lampada ad alcol; condizione buona; ₤ 6».
Il dispositivo era usato per mostrare la forza sviluppata dalla contrazione in lunghezza della sbarra di acciaio durante il raffreddamento.
Esso è formato dalla massiccia sbarra di acciaio a sezione quadrata che poggia sulla robusta base tramite i due sostegni.
La maniglia serve per serrare fortemente la sbarra alla cui estremità opposta c’è un occhiello.
In questo esemplare oggi si trova infilato all’occhiello un tubetto di rame, ma per una spettacolare dimostrazione vi si poneva un cilindretto di ghisa.
Per eseguire la dimostrazione si riscaldava fortemente la sbarra di acciaio, senza la maniglia, sopra un fornello a carbone o sopra un becco di gas, senza però arroventarla.
La sbarra, presa con opportune pinze, veniva posta sui sostegni. Poi si introduceva nell’occhiello della sbarra il cilindretto di ghisa, si applicava la maniglia e la si ruotava fino a che si stringeva fortemente. Dopo un po` di tempo, per la contrazione della sbarra dovuta al raffreddamento, il tondino di ghisa si rompeva di schianto mostrando l’intensità della forza sviluppata.
Le figure sono state tratte da cataloghi della Max Kohl editi nella stessa epoca dell’esemplare del Montani.
La figura 54795 è tratta da Max Kohl A. G. Chemnitz (Germany), Price List No-50,Vols. II and III.
Physical Apparatus, pag. 568 senza data. Rinvenibile all’indirizzo:
https://www.sil.si.edu/DigitalCollections/trade-literature/scientific-instruments/pdf/sil14-51634.pdf
 La figura 799 N° 32177 è tratta da Appareils de Physique, Max Kohl Chemnitz Saxe, Catalogue n° 22. 1905; a pag. 214 si legge: «Appareil de Tyndall, fig. 799, pour montrer la dilatation par la chaleur et la contraction par le froid; avec une douzaine de barreaux de fonte . . . Au mojen d’un certain nombre des becs Bunsen, on chauffe le barreau rectangulaire jusqu’à la temperature de recuit; on introduit à l’extrémité un barreau de fonte de 9 mm de diamètre, puis on le visse dans le bâti et on le laisse refroidir. Au bout d’un moment, les barreaux se brisent avec violence».
 Che si trova all’indirizzo:
http://cnum.cnam.fr/CGI/redir.cgi?M9901
o all’indirizzo:
http://cnum.cnam.fr/PDF/cnum_M9901.pdf
 Le figure 91014 e 91011 sono tratte dal Preiliste Nr. 100, Band III. Physikalische Apparate, . . . Max Kohl A. G. Chemnitz, del 1905, che si trova all’indirizzo:
https://vlp.mpiwg-berlin.mpg.de/library/data/lit21186?
Esse si trovano a pag. 690 dove si legge:
«91011. Kontraktionsapparat nach Tyndall, Figur, um die Ausdehnung durch Erwärmung und die Elementargewalt bei der Zusammenziehung durch Abkülung zu demonstrieren ( M. P. II, Fig. 34 und 35 [II, 2, Fig. 32 und 33]), mit 12 Gußeisenstäben . . . Durch Wiederzusammenziehen des starken, vierkantigen Stabes nach der Erhitzung wird ein 9 mm starker Gußeisenstab gesprengt. Bunsenbrenner und Erhitzungsgestell siehe die folgenden Nummern».
«91014. Kontraktionsapparat, Figur, mit Fletcher-Brenner, ohne Erhitzungsgestell zu verwenden».

Foto di Claudio Profumieri e Ilaria Leoni, elaborazioni, ricerche e testo di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.

 

 

 

Apparecchio centrifugo con due sfere scorrevoli.
Nell’inventario D del 1956 al n° 949 si legge: 
“Apparecchio con due sfere scorrevoli per esperimenti sulla forza centrifuga”.
Anteriore dunque al 1956 esso porta due sfere di massa diversa, legate fra loro con una cordicella. Le sfere di legno forate scorrono con basso attrito lungo un`astina montata su un sostegno.
Il dispositivo è didatticamente molto interessante per illustrare tre argomenti: 1) mette in evidenza l’importanza del centro di massa delle due sfere; 2) pone il problema dei sistemi di riferimento; 3) simula, ma solo all’equilibrio, un sistema rotante come quello Terra – Luna.
Per chi è interessato ai sistemi di riferimento, rimanendo nell’ambito della fisica “classica”, è un buon esercizio completare la descrizione degli schemi delle forze in gioco che, nel testo che segue, sono volutamente incompleti. Egli scoprirà che i fenomeni in esame sono un po’ più complessi di come sembra a prima vista in un dispositivo così semplice.
Si chiederà ad esempio perché un oggetto di massa m posto in rotazione tende ad allontanarsi dal centro di rotazione.
Se si pone nel sistema di riferimento non inerziale attribuirà il fenomeno alle forze centrifughe; ma ne seguirà la domanda: “qual’è la causa di queste forze?”.
Se si pone nel sistema di riferimento inerziale attribuirà il fenomeno all’inerzia: ma ne seguirà la domanda: “qual è l’origine dell’inerzia?”.
Per curiosità si può vedere anche l’Apparecchio per la dimostrazione dello schiacciamento polare della Terra, scrivendo “polare” su Cerca.
Per eseguire la prova, una volta posto l`apparecchio sulla macchina rotante, si procede per tentativi per trovare il centro di massa delle due sfere.
La situazione di equilibrio, e la conseguente rotazione delle due sfere, si ottiene quando il centro di massa coincide col centro di rotazione.
Si posizionano dunque le due masse col filo tirato come mostrato nelle foto e nelle figure e si avvia la rotazione aumentando il numero di giri.
Più ci si avvicina alla situazione di equilibrio più diventa necessario aumentare la velocità angolare poiché il lieve attrito tra i fori nelle sfere e la barretta trattiene inizialmente in rotazione le sfere. Dopo di che, se la posizione scelta è errata, entrambe le sfere vengono proiettate verso l`uno o l`altro dei due bordi; se invece si ottiene l`equilibrio le sfere mantengono la loro posizione iniziale anche per un numero di giri relativamente elevato.
Per chiarire meglio quanto detto, le cose vanno viste da due sistemi di riferimento. In quello  non inerziale si vedono due forze centrifughe ognuna agente su una massa  (in questo sistema non c`è rotazione poiché l’osservatore è nel sistema).
All`equilibrio, cioè quando si vedono, dal sistema inerziale, le due sfere ruotare indisturbate, significa che nel sistema non inerziale le due forze centrifughe sono uguali e opposte e dunque si ha F₁ = F₂ , cioè m₁ · ω² r₁ = m₂ · ω² r₂; da cui  m₁ r₁ = m₂ r₂.
Dove r₁ ed r₂ sono le distanze dal centro di rotazione, come si vede nella figura 172, e ω è la velocità angolare.
Nel sistema della stanza (considerato approssimativamente inerziale) all’equilibrio si osservano soltanto le due forze centripete dovute al filo (ognuna applicata ad una massa) che  provocano il moto circolare.

 La figura 172 è tratta da E. Perucca, Guida pratica per esperienze didattiche di Fisica Sperimentale, N. Zanichelli, Bologna 1937.

La figura 859 è a pag. 75 del Catalogue M May 1909 Physical and Chemical Apparatus for Science Laboratories
Central Scientific Co., Chicago U.S.A. . Rinvenibile all’indirizzo:
https://www.sil.si.edu/DigitalCollections/trade-literature/scientific-instruments/pdf/sil14-51679.pdf

La figura 100 è tratta  da L. Segalin, Fisica sperimentale, Vol. I, G. B. Paravia & C., Torino 1933.  
Foto di Claudio Profumieri, elaborazioni, ricerche e testo di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.

 

 

Spettrometro mod. M.G.1.
L`inventario D del 1937, in data 7 novembre 1955, riporta l`acquisto di uno “Spettrometro modello N completo” costruito dalle Officine Galileo-Firenze. Il numero di matricola è O61a 00117.

Nel 1931 Oreste Murani, descrive brevemente lo spettrometro di Hilger in cui è facile riconoscere l`esemplare del Montani. Il modello M.G.1 è il perfezionamento di uno spettrometro che le Officine Galileo di Firenze costruivano già nel 1933.
Il suo cuore è il prisma di Pellin-Broca, in vetro flint extra denso a grande dispersione (indice di rifrazione 1,64). Divisibile idealmente in tre prismi, esso ha la caratteristica di rifrangere il raggio di luce sempre ad angolo retto rispetto al raggio incidente, qualunque sia l`angolo di incidenza.

Il prisma è alloggiato sopra una piattaforma ruotante racchiusa in una scatola con un coperchio amovibile. Ciò permette di far ruotare il prisma (invece degli apparati ottici), per mezzo di un tamburo cilindrico a vite di precisione, applicato sul fianco, per esplorare lo spettro da 380 nm a 800 nm; il valore della lunghezza d`onda della riga inquadrata nel reticolo si legge sul tamburo graduato. I due robusti bracci cilindrici, i cui assi sono complanari e perpendicolari, presentano: il primo un collimatore con fenditura variabile a vite micrometrica fino a 0,01 mm, il secondo un cannocchiale astronomico con reticolo a croce. Le sorgenti di luce da esaminare sono fornite da lampade a gas poste nell`edicola.
La differenza sostanziale tra uno spettroscopio e lo spettrometro di Hilger consiste nella facilità con cui si possono misurare le lunghezze d’onda delle righe spettrali. Una volta regolati bene sia la larghezza della fenditura, sia la messa a fuoco del telescopio, è sufficiente ruotare il tamburo, sul quale è incisa una scala graduata a spirale tarata in nm, inquadrare la riga che interessa all’incrocio del reticolo ottico che appare nel campo visivo, e leggere il valore della sua lunghezza d’onda sulla scala. La taratura dello spettrometro si può eseguire usando lampade nelle quali sono presenti gas noti i cui spettri sono ben conosciuti. Si scelgono vari tipi di gas in modo che permettano la taratura su tutto il range di misura. Esistono apposite tabelle di elementi, nelle quali sono riportate per ogni riga dell’elemento la colorazione della riga (che è solo orientativa) e la lunghezza d’onda.
Nelle Istruzioni delle Officine Galileo si legge testualmente: «MONOCROMATORE – SPETTROMETRO M.G.1 (Dimensioni: cm 40 × 50 × 85 – Peso: Kg 15,400)
Generalità
Lo strumento appartiene alla categoria dei monocromatori – spettrometri a deviazione costante di 90 °. Parte ottica fondamentale dei medesimi è un prisma di Pellin- Broca in flint extra denso (n_D = 1,64) a grande dispersione montato sopra una piattaforma girevole racchiusa in una scatola metallica di forma parallelopipeda. La scatola è sorretta da una colona regolabile in altezza, su basamento a treppiede, ed ha un coperchio amovibile per eventuali ispezioni e sostituzioni.

Perpendicolarmente a due facce laterali contigue della stessa scatola, orientate a scrupolo come le facce
di entrata e di uscita del prisma, si protendono infuori due robusti bracci cilindrici i cui assi sono, per costruzione, complanari e perpendicolari. Per il montaggio dello strumento come monocromatore trovano alloggio in detti bracci i due collimatori C₁ e C₂; per quello come spettrometro vengono invece apllicati il collimatore di entrata C₁ ed un cannocchiale astronomico con reticolo a croce C₃, in funzione di collettore. Questi diversi strumenti sono intercambiabili, presentano richiami a nasello per il bloccaggio e sono muniti di obiettivi “trattati” con ø = 21 mm, f = 204 mm, apertura relativa 1 : 9.
In corrispondenza dei piani focali degli obiettivi dei collimatori C₁ , C₂ sono sistemate due fenditure F₁, F₂. la loro grandezza è regolabile mediante viti micrometriche (che spostano simmetricamente ambedue i lembi delle fenditure) ed è misurabile, su un apposito tamburo graduato, con l’approssimazione di 0,01 mm.
Per il montaggio dello strumento come spettrometro occorre sostituire al collimatore C₂ il cannocchiale astronomico C_3».
Seguono altre sei pagine di istruzioni.
Vi si dice fra l’altro che lo spettrometro ha un alto potere separatore: 1 : 1300.
In fondo si legge: «Lunghezza d’onda delle radiazioni più comuni e più consigliabili per la taratura dello strumento. Fiamma e arco al sodio: 2 righe gialle (vicinissime) 5890 Å e 5896 Å. Arco e mercurio: 1 riga verde (oltre il resto) 5461 Å. Tubo di Plücker e idrogeno: 3 righe: rosso 6563 Å azzurro 4861 Å violetto 4340 Å. Tubo di Plücker a elio: 1 riga gialla (oltre il resto) 5876 Å. [Å nella notazione qui usata è l’angström = 10 ^-10 m N.d.R.] (vedi relativa tabella X-3)».

Come si vede nella figura 9002-4 esistono due tipi di tubi di Plücker. Uno si può riempire col gas che si desidera, l’altro si acquista scegliendone le caratteristiche.
Nella figura X-5 si osserva il meccanismo di comando per ruotare il prisma di Pellin Broca, collegato al tamburo.
Inizialmente questo modello veniva prevalentemente usato come monocromatore. Infatti, se si sostituisce il cannocchiale astronomico con un collimatore, si può isolare una riga di un solo colore da sorgenti di luce a spettro a righe. In tal caso esso diventa un fornitore di luce monocromatica del colore desiderato. Nel caso di sorgenti di luce a spettro continuo, il raggio emergente comprende una regione tanto più ristretta quanto più è sottile la fenditura del collimatore.
L’avvento dei laser, la cui luce ha caratteristiche nettamente superiori, lo ha reso obsoleto come monocromatore, limitandone l’uso didattico alla spettroscopia, uso nel quale si rivela molto più semplice e preciso di uno spettroscopio.

La figura L 923 del modello tipo N si trova a pag. 214 del catalogo: Apparecchi per l’Insegnamento della Fisica a cura del prof. R. Magini, Officine Galileo, 1940.
Bibliografia:
O. Murani, Trattato elementare di Fisica, vol. II U. Hoepli Milano 1931; da cui sono tratte le figure 166 (prisma di Pellin-Broca) e 167 (tamburo).
E. Perucca, Fisica generale e sperimentale, vol. II UTET Torino 1934; da cui è tratta la figura 77 molto particolareggiata.
La figura 1 del monocromatore è a pag. 3 e la figura 2 dello spettrometro è a pag. 4 delle Istruzioni: Monocromatore – Spettrometro M.G.1 delle Officine Galileo.
La suggestiva figura 8 è a pag.7 di Notizie per i laboratori scientifici e industriali a cura delle Officine Galileo – Firenze N. 73 – Luglio 1933. Spettroscopio/Spettrografi.”
Spettroscopio modello piccolo.
La descrizione di un modello simile a questo si può trovare in Notizie per i laboratori scientifici e industriali, a cura delle Officine Galileo-Firenze n° 73 del luglio 1933; da cui abbiamo tratto una figura.
Il capitolo decimo “Spettroscopia”, interamente dedicato all’uso degli spettrografi e spettrometri, si trova in: M. Panitteri, S. Barcio. D. Marucci, Complementi di Fisica
e Laboratorio, G. B. Paravia & C., Torino, 1967. Da esso sono tratte le figure X-5 e X-4 dello spettrometro di Hilger e del prisma di Pellin Broca di pag. 137. La tabella
X-3 di pag. 145 riporta i risultati della taratura di uno spettrometro.
Nel disegno del prisma di Pellin-Broca, che si trova per altro in numerosi testi, è rappresentato il percorso di un “raggio” luminoso.
Le figure del tamburo graduato e dei tubi di Plücker si trovano in numerosi libri e cataloghi; qui si sono scelte: la fig. 1 di pag. 402 e la fig. 9002-4 di pag. 406 del
catalogo Physical Apparatus, Baird & Tatlock (London) Ltd. 1912. Rinvenibile all’indirizzo:
https://www.sil.si.edu/DigitalCollections/trade-literature/scientific-instruments/pdf/sil14-52548.pdf

Se si desidera consultare la scheda riguardante il monocromatore M.G.1, si può scrivere “M.G.1” su Cerca.
Foto di Daniele Maiani e di Federico Balilli, elaborazioni, ricerche e testo di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.