Categoria: fisica

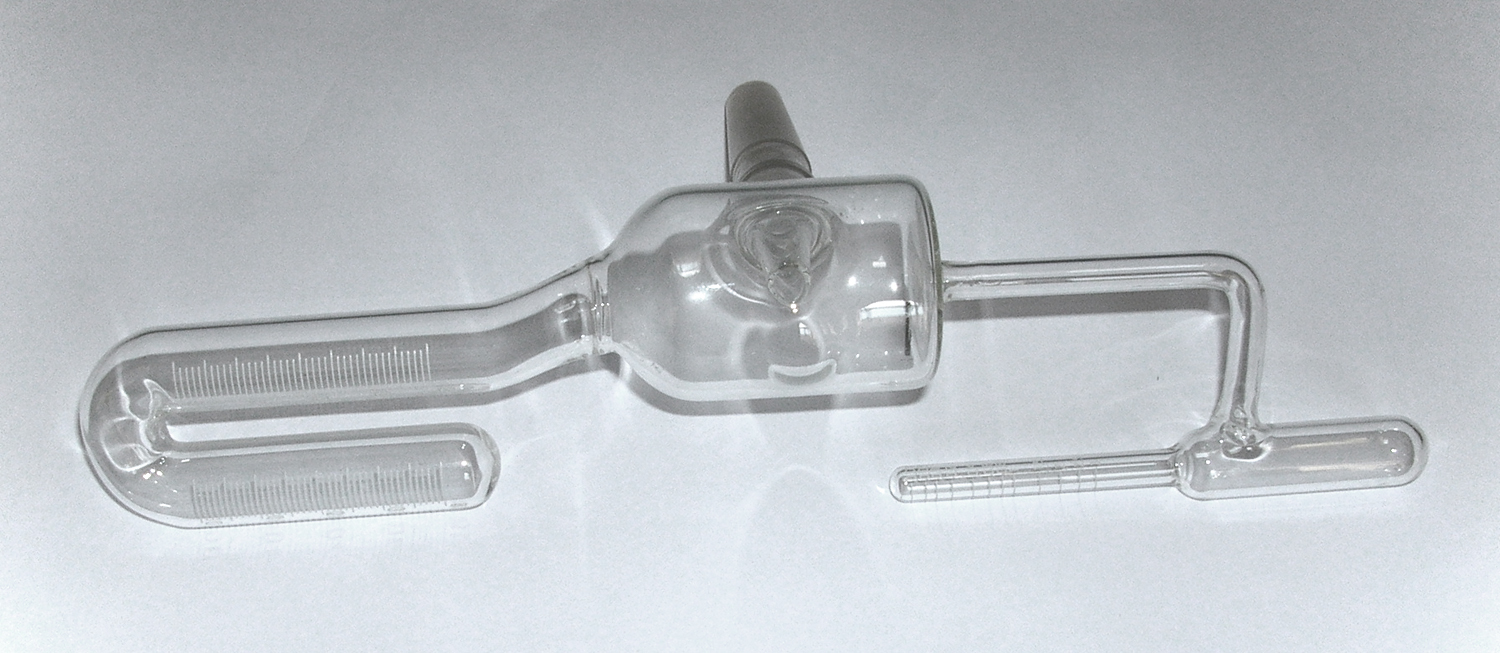
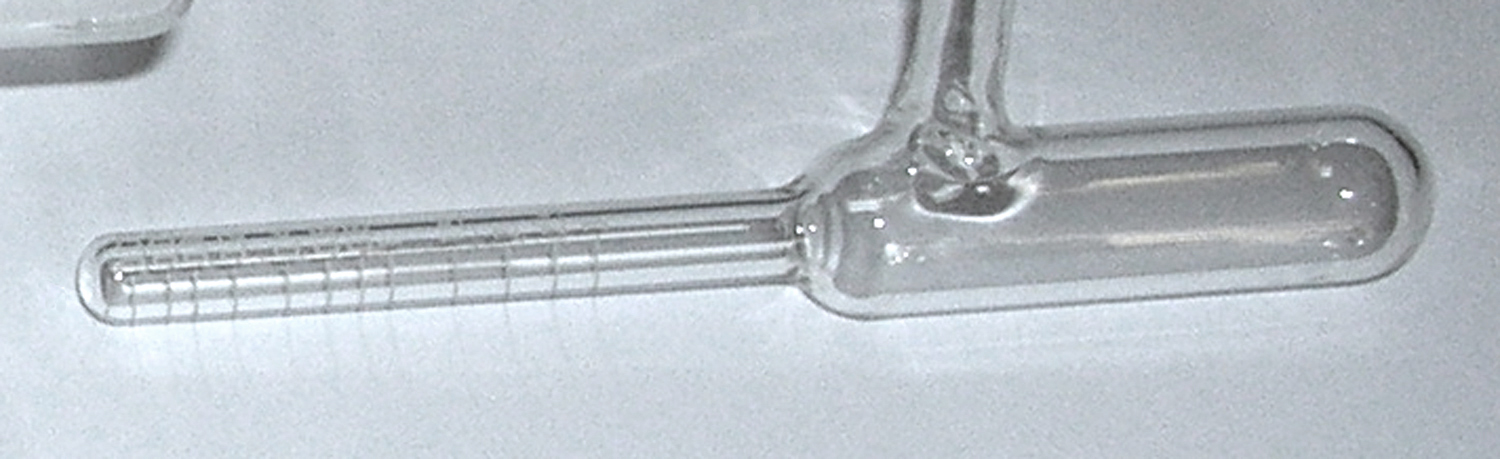
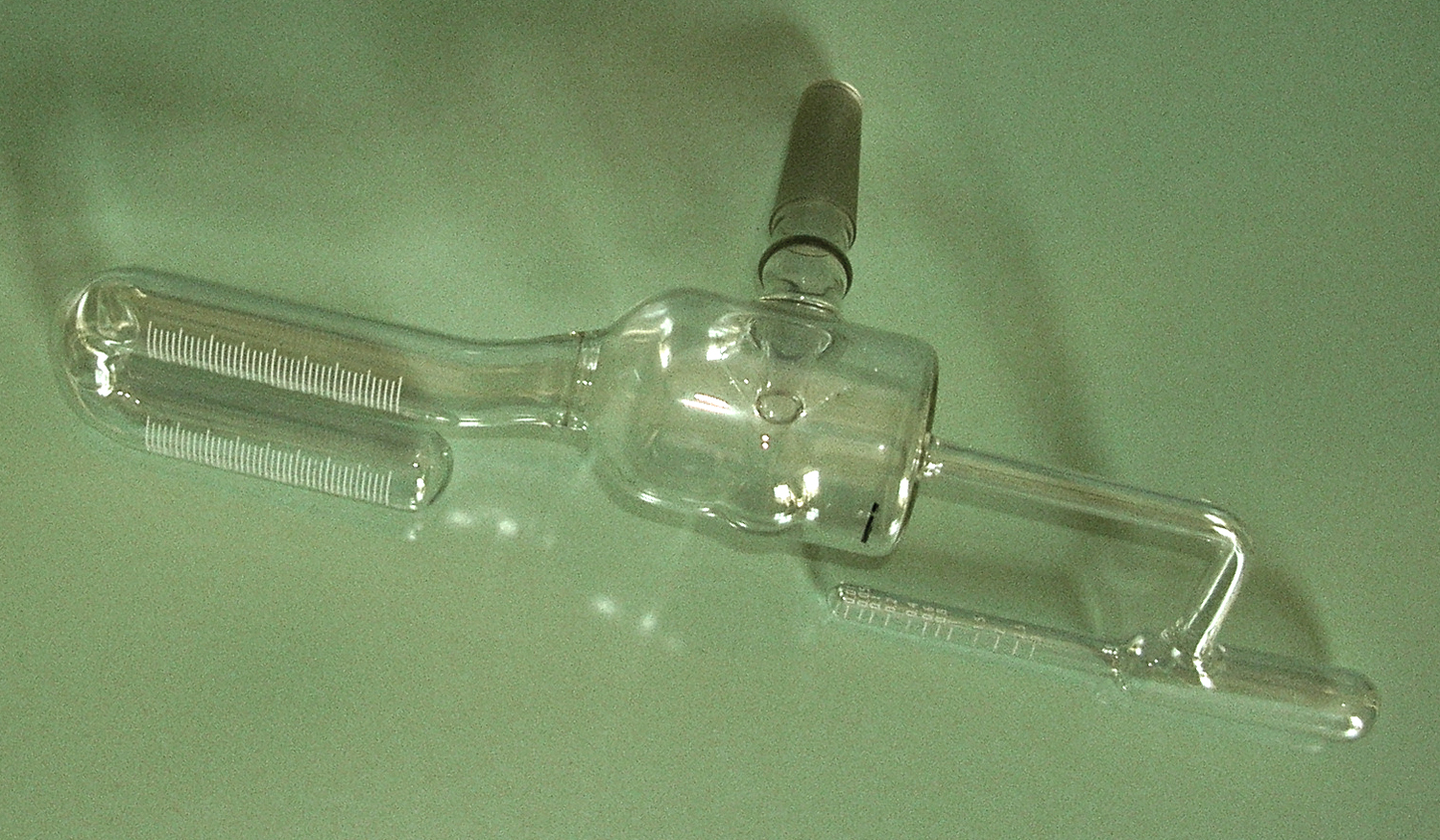
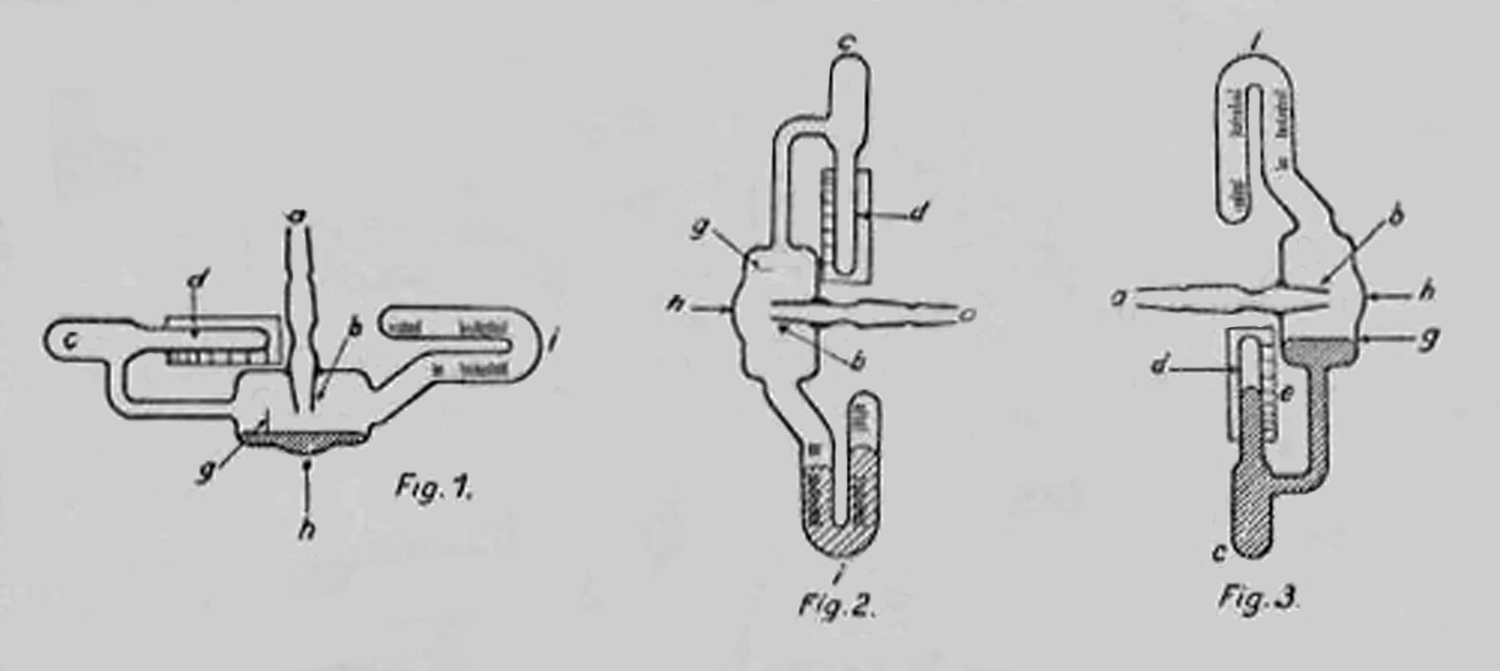
              Emisferi di Magdeburgo G. B. Paravia.
Questo esemplare è stato donato nel novembre del 2014 dal Sig. Roberto Oss di Trento al Montani, tramite Fabio Panfili. Lo ringraziamo.
Se ne ignora la data di fabbricazione.
Esso è di piccole dimensioni e manca di una maniglia che si avvitava nell`emisfero superiore.
Gli emisferi furono ideati e realizzati da Otto von Guericke (1602-1686), che fu borgomastro della città di Magdeburgo (di qui il loro nome) in Germania.

Numerose fonti storiche narrano che nel 1657 un gruppo di 8 cavalli per parte non riuscì a dividere i due emisferi, una volta che al loro interno fu fatta una buona rarefazione dell`aria con la pompa anch`essa ideata e costruita da von Guericke nel 1650. Gli emisferi erano di bronzo ed avevano un raggio di 0,36 m.
Von Guericke calcolò che la forza necessaria per dividerli doveva essere almeno di 12.000 N [Abbiamo trasformato le unità di misura usate da von Guericke in quelle del S. I.]. Un breve calcolo molto approssimato ci suggerisce che la pompa di von Guericke non faceva un buon vuoto e vi era una discreta pressione residua della quale egli era ben conscio, ma la prova riuscì ugualmente.
Con esperimenti di questo tipo si mostravano sia l`effetto della pressione atmosferica, sia l`esistenza del vuoto  (inteso come quasi assenza di gas).
Gli emisferi di Magdeburgo divennero, nel corso del XIX e anche del XX secolo, uno degli esperimenti classici da eseguire nelle scuole.
Nel Laboratorio di Fisica del Montani c’è un esemplare funzionante che viene tuttora usato per la dimostrazione che descriveremo; la differenza costruttiva principale di questo consiste nelle maniglie saldate agli emisferi e nell`incavo nel quale si posiziona un anello di gomma. Si deve subito far osservare che i due emisferi, che combaciano perfettamente, una volta uniti, si possono separare con estrema facilità.
Non vanno usati né grasso né sostanze adesive.
Dunque si uniscono i due emisferi e si posiziona il rubinetto con la chiavetta disposta in senso verticale. Si appoggia poi la base sul disco di gomma della pompa e la si aziona per qualche minuto.
All`inizio è bene premere leggermente sull`emisfero superiore per facilitare l`operazione. Quindi si chiude il rubinetto (chiavetta orizzontale) e si toglie l`apparecchio dal disco. Si noterà che a volte questa manovra richiede un discreto sforzo. Poi si invitano due allievi a separare i due emisferi tirando in versi opposti.
È naturale la loro meraviglia nel constatare che non riescono nell`intento.
Basta infine aprire leggermente il rubinetto per far entrare l`aria e le due parti come per incanto si separeranno agevolmente.
Bisogna accuratamente evitare che gli emisferi in questa fase cadano a terra poiché si possono danneggiare divenendo inservibili. Se il danno è minimo si può eventualmente ricorrere ad una tornitura ben fatta e successiva smerigliatura.
 Si noti che gli emisferi di questo esemplare sono avvitati uno alla base e l`altro alla maniglia. Anche il rubinetto è avvitato. Occorrono dunque delle guarnizioni adatte. All`epoca si usavano rondelle di sottile cuoio ben conciato, imbevuto di olio e spalmato di grasso minerale.
 Nel foglio “Istruzione N. 159” della Paravia, forse risalente ad un`epoca lievemente posteriore a quella stimata per questo esemplare, si raccomanda di non usare rondelle fatte di altri materiali come fibra, gomma, plastica, ecc. .
Se l`insegnante vuole approfondire di poco l`argomento può far fare un calcolo molto approssimato della forza necessaria a separare i due emisferi.
Supposto che la pompa faccia una buona rarefazione, e che vi sia una buona tenuta d`aria, si misura il diametro della sfera e quindi si calcola la superficie del cerchio massimo (poiché le forze dovute alla pressione atmosferica sono perpendicolari alla superficie sferica, questo trucco serve per ottenere una stima approssimata della forza risultante che bisogna vincere per separare gli emisferi). Poi si moltiplica detta superficie per la pressione atmosferica standard (101.300 Pa) e si ottiene la forza di cui si parlava prima, dovuta al peso dell`aria sovrastante. È ovvio che la forza vera da applicare sarà minore per l`effetto dell`aria residua nella sfera.
La meraviglia che destano simili esperimenti è dovuta al nostro vivere immersi nell`aria che nasconde la consapevolezza del peso dell`aria stessa.
Evangelista Torricelli fu il primo a scrivere chiaramente su questo argomento.
Otto von Guericke costruì pure un barometro ad acqua accanto alla sua casa, e si racconta che vi galleggiasse una papera di legno. Quando la pressione atmosferica era alta, la papera superava il tetto della casa ed era bel visibile al viandante.
Il primo a realizzare un tal barometro fu Gasparo Berti a Roma nel 1640 (e quindi tre anni prima di Torricelli che usò il mercurio) e quel barometro deve essere più alto di 11/12 metri (mentre quello di Torricelli è alto un metro). La stampa originale visibile nella quarta immagine è conservata presso il Deutsches Museum di Monaco, insieme agli emisferi di Otto von Guericke, si trova inoltre nel libro di G. Schott, Mechanica hydraulico-pneumatica, Würzburg 1657.
Se si desidera avere informazioni sui barometri di Torricelli o di Fortin, basta scrivere “Barometro” su Cerca.
Foto di Claudio Profumieri, elaborazioni, ricerche e testo di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.

 

 

 

 

Rocchetto di Ruhmkorff Leybold-Heraeus, made in Germany. Matricola N° 521 02. Tensione di alimentazione in C.C. 6/8 V.
Nell`inventario D del 1956 al n° 5008 in data 31 dicembre 1970 è registrato come “rocchetto di induzione”.
Il piccolo esemplare è perfettamente funzionante, come si vede dalla scintilla in alcune  foto, mentre è alimentato da una batteria.

Il rocchetto di E. D. Ruhmkorff (1803-1877) ha avuto un diffusissimo impiego dall`anno della sua invenzione (1851) come generatore di alta tensione.
Era infatti usato per alimentare: i tubi per la produzione dei raggi X in campo medico, i tubi a scarica o a vuoto nelle ricerche scientifiche, l`oscillatore di Hertz, le bottiglie sintoniche di Lodge, ecc. .
Era inoltre l`alimentatore dell`oscillatore di Righi nel primo trasmettitore radio di Marconi.
Secondo F. Cajori esso fu inventato da C. G. Page (1812-1868) nel 1838 negli Stati Uniti.
Ma evidentemente l`invenzione nel 1851 non era nota in Europa.

Il rocchetto di Ruhmkorff è essenzialmente un trasformatore, con un primario costituito da un numero esiguo di spire avvolte su un nucleo ferromagnetico (spesso costituito da fili di ferro) e da un secondario (generalmente diviso in due avvolgimenti separati, costituiti da numerosissime spire e collegati in serie) avvolto sul primario.
Ma mentre un normale trasformatore viene alimentato in corrente alternata, il rocchetto è alimentato da una batteria di pile o di accumulatori, oppure da un alimentatore in C.C., la cui corrente continua viene interrotta bruscamente e periodicamente.
Il più comune dispositivo usato è l`interruttore elettromagnetico a martelletto di Neef, dello stesso tipo dei vecchi campanelli elettrici.
Non appena circola corrente nel primario, il martelletto viene attratto cosicché apre il circuito; la corrente cessa e il martelletto viene richiamato nella sua posizione di riposo dall`asticina elastica di cui è fatto, chiudendo di nuovo il circuito. Questo processo avviene più volte al secondo, ma il funzionamento è capriccioso e richiede una paziente messa a punto.
Per sommi capi, una rapida variazione della corrente al primario genera un flusso di campo magnetico rapidamente variabile che si concatena al secondario, generando in questo una forza elettromotrice indotta di notevole intensità. La tensione all`uscita del rocchetto presenta una semionda a bassa tensione e una semionda con un picco di tensione stretto e molto elevato che ne fa la caratteristica principale per i suoi impieghi.
Bibliografia.
F. Cajori, Storia della fisica elementare, Zanichelli, Bologna 1908.
G. Bruhat, Cours d`électricité, Masson & C., Paris 1924. L. Olivieri ed E. Ravelli, Elettrotecnica, Vol. I, CEDAM, Padova 1959.
 Foto di Claudio Profumieri, elaborazioni, ricerche e testo di Fabio Panfili.
Per ingrandire le imagini cliccare su di esse col tasto destro del mouse e scegliere tra le varie opzioni.

 

 

 Serie di cinque cilindri di acciaio per il limite dell`udibilità dei suoni, Off. Galileo, Firenze.
La serie, negli inventari più recenti, si trova sia al n° D 6187 registrata in data 23/08/1972 dove si legge: “Serie di 5 verghe elastiche”, sia in data 26/09/1972 dove si legge di nuovo: “Serie di 5 verghe elastiche” al costo di ₤ 31.700. Inoltre la serie si trova nel Catalogo delle Officine Galileo del 1957 a pag. 62.
In dotazione vi è un martelletto in lega metallica per la percussione.
I cinque cilindri di acciaio inox sono tenuti da due cordoncini che terminano in una maniglia di legno. Elenchiamo la loro lunghezza e frequenza: L<sub>1</sub> = 21,1 cm f<sub>1</sub> = 2048 Hz; L<sub>2</sub> = 14,6 cm f<sub>2</sub> = 4096 Hz; L<sub>3</sub> = 10,2 cm f<sub>3</sub> = 8192 Hz; L<sub>4</sub> = 7,2 cm f<sub>4</sub> = 16384 Hz; L<sub>5</sub> = 5,1 cm f<sub>5</sub> = 32768 Hz.
Il loro diametro è calibrato ed è di 2 cm.
Le istruzioni del catalogo dicono che le lunghezze decrescono in progressione geometrica con ragione 1/ √ 2 (1/radice di 2), ma è sufficiente fare qualche calcolo per osservare che nella realizzazione pratica le lunghezze sono state aggiustate per ottenere le volute frequenze che sono le quattro ottave successive del Do<sub>7</sub> di 2048 Hz.
L`esperienza consiste nel percuotere al centro e in successione i cilindri partendo da L₁ che genera una nota intensa, mentre le note di L₂ e di L₃ sono più deboli e sibilanti; raramente gli adulti odono la nota di L₅, mentre in genere i ragazzi la sentono distintamente.
L`ultima nota verrebbe udita dai gatti e dai cani che normalmente non sono presenti all`esperimento.
Nella letteratura dei primi del Novecento citata in bibliografia, si leggono formule nelle quali la frequenza è inversamente proporzionale al quadrato della lunghezza.
Si noti che le formule rinvenibili nella letteratura attuale differiscono da quelle antiche solo per i coefficienti. Dunque, a parità del diametro e del materiale impiegato, il prodotto di ogni frequenza per il quadrato della rispettiva lunghezza della barretta dovrebbe essere costante.
Ma, come si è già detto sopra, anche in questo caso basta fare qualche semplice calcolo per avere la conferma dell`aggiustamento delle lunghezze da parte del costruttore per ottenere le frequenze volute.
Abbiamo riportato un disegno che illustra il modo fondamentale di vibrazione di un cilindro pieno secondo la letteratura attuale; si notino le posizioni dei nodi al 22,4 % della lunghezza: la semilunghezza d`onda risulterebbe del 55,2 % della lunghezza della barretta. Di nuovo succede che il prodotto della lunghezza d`onda per la frequenza dovrebbe fornire la velocità dell`onda trasversale nell`acciaio inox ma i valori risultanti sono decrescenti e inattendibili.
La figura H 737, corredata da una breve spiegazione, si trova a pag. 151 di Apparecchi per l’Insegnamento della Fisica, a cura del prof. R. Magini, Officine Galileo, 1940.
Bibliografia: la letteratura sulle verghe elastiche è molto vasta.
Noi citeremo due autori marchigiani:
Oreste Murani, nato a Monterubbiano (1853-1937) professore di Fisica all`Università oggi detta Politecnico di Milano e amico di amico di Temistocle Calzecchi Onesti;
Angelo Battelli, nato a Macerata Feltria (1862 – 1916), professore in diverse Università italiane ed eminente politico.
O. Murani,  Trattato Elementare di Fisica, Vol. I, U. Hoepli, Milano 1905.
A. Battelli e P. Cardani, Trattato di Fisica Sperimentale, Vol. II, F. Vallardi, Milano 1913.
Foto di Claudio Profumieri, elaborazioni, ricerche e testo di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.

 

 

 

 

 

 

ABSTRACT: Beccaria – Coulomb`s sphere.
Dated 1925, manufactured by “Officine Galileo”, Florence.
The metal sphere is hollow and has got a hole at the top, the supporting stick is made of an insulating resin. Its didactic use is to show that within a conductor there are no electric charges in excess and thus the electric field is zero. To carry out the experimental demonstration it is necessary to charge a little ball made of elder pith hanging to an insulating wire and then to lower the ball through the hole. If the ball keeps inside, its charge shows itself outside the sphere due to electric induction. If the ball comes into contact with the metal, then its charge will be transferred to the outside of the sphere and the ball will discharge. If we introduce once again the little ball inside the sphere , we place it in contact with the internal surface of the sphere and then we pull it out again, we will notice that the little ball has picked up no electric charges. The measurement of electric charges is carried out through an electroscope.
Traduzione di Veronica Rosa, supervisione della prof.ssa Meri Biancucci.        Sfera di Beccaria-Coulomb.
Nell`inventario generale n° 6 del 1925 al n° 2241/140 di pag. 68 si legge: “Officine Galileo Firenze Sfera metallica isolata. ₤ 86”. Destinata al Gabinetto di Fisica. Nell`inventario del 1927 al n° 659 – 2241 si legge di nuovo: “Sfera metallica isolata; ₤ 86”.
Nell`inventario D del 1937 ha il n° 376 dove è detta. “Sfera cava di Coulomb”. Della ditta Officine Galileo Firenze, reca il N° 100281, costo ₤ 80.

 La sfera di metallo è cava e presenta un foro sulla sommità, l`astina di sostegno è di resina isolante.
Didatticamente serve per mostrare che all’interno di un conduttore non esistono cariche elettriche in
eccesso e quindi il campo elettrico è nullo, come ci si aspetta dalla comprensione della legge di
Coulomb. Questa è una “prova di zero”, ed ha la sua particolare precisione.
Ne segue che il 2 che compare come esponente di D nella
legge di Coulomb è 2 a meno di una parte su un miliardo; da ciò deriva il secondo nome che usualmente
si da alla sfera.  La legge di Coulomb (formalmente analoga a quella di Newton F = G (M m) / D² ) è la seguente:
F = K (Q q) / D².
Dove F è la forza tra due cariche elettriche puntiformi Q e q poste ad una distanza D. K vale 8,987552 10<sup>9</sup> N m² / C².
 Ma la sorprendente analogia tra le due leggi è nel loro aspetto matematico, non nei significati fisici.
Esperimenti più sofisticati hanno confermato la validità della considerazione sull`esponente 2.
L`importanza del valore di questo esponente è legata alla massa che si attribuisce al fotone che, nella fisica moderna, è il messaggero dell`interazione elettromagnetica forte. Una massa nulla significa distanza di interazione infinita e velocità del fotone pari a c nel vuoto, qualunque sia l`energia trasportata.
Se il fotone avesse una massa pur estremamente piccola, la sua velocità sarebbe minore di c e dipenderebbe dalla sua energia: una maggiore energia corrisponderebbe a una maggiore velocità, comunque sempre inferiore a c. Si avrebbero fotoni lenti e fotoni veloci, cioè se una luce bianca partisse ad un dato istante da una sorgente lontanissima, vedremmo prima i colori violetti poi via via arriverebbero tutti gli altri per finire coi i rosso scuri.
Le equazioni di Maxwell sarebbero sostituite dalle equazioni di A. Proca e l`intero Universo sarebbe diverso da quello che conosciamo. Per la dimostrazione sperimentale, dopo aver misurato con l’elettroscopio che la sfera è scarica, si carica una pallina di midollo di sambuco, appesa ad un filo isolante, e la si cala attraverso il foro. Se la pallina staziona all’interno, la sua carica si rivela all’esterno della sfera per induzione elettrica, come si osserva all’elettroscopio.
Se poi la pallina viene posta a contatto col metallo, la sua carica si trasferisce all’esterno della sfera ed essa si scarica, come risulta da una misura successiva con l’elettroscopio.
Introducendo di nuovo la pallina scarica dentro la sfera carica, e mettendola in contatto con la parete interna, alla successiva estrazione si nota che nessuna carica è stata acquisita dalla pallina; mentre l’elettroscopio segna la presenza di cariche sulla superficie esterna della sfera.
In genere gli storici della fisica più noti tendono a trascurare i lavori pionieristici di G. B. Beccaria (1716 – 1781), dunque si legge che fu B. Franklin nel 1755 ad osservare per primo che una sferetta di sughero, posta all`interno di una semisfera cava metallica carica, non viene attratta dalla superficie interna. Franklin ne diede notizia a J. Priestley. Costui nel 1767, per trovare una spiegazione al fenomeno scoperto da Franklin, si ispirò ad un lavoro di Newton sull`assenza di forze di gravità all`interno di un guscio sferico di materiale omogeneo, e dunque ipotizzò che le forze elettriche agiscono con una legge dell`inverso del quadrato della distanza.
  Prima di C. A. Coulomb, J. Robison verificò sperimentalmente la legge, ma pubblicò i risultati nel 1881, dopo Coulomb.
Subito dopo nel 1773 H. Cavendish eseguì un esperimento con due sfere metalliche concentriche, collegate con un filo conduttore. Si caricava la sfera esterna, si toglieva il filo tra le due sfere e si misurava la carica sulla sfera interna. Questa è una misura di zero, molto più precisa delle altre. Infatti nel 1936 S. J. Plimpton e W. E. Lawton ripeterono sostanzialmente l`esperimento di Cavendish. Coulomb ebbe i meriti di verificare la legge sia con cariche di segno uguale, sia di segno opposto, a distanze diverse, ottenendo una precisione del 10% peggiore di quelle ottenute da Robison e Cavendish, ma pubblicò i suoi lavori nel 1788, ben prima di loro.
Ma cosa accade se la forma del conduttore cavo non è sferica? Esperienze come il Pozzo e la Gabbia di
Faraday mostrano come la forma può essere qualunque, purché la superficie sia chiusa e che questa non
deve necessariamente essere continua.
Infatti nel caso della gabbia è sufficiente che le maglie della rete siano fitte per ottenere uno schermo elettrostatico. Infine, se il conduttore cavo chiuso viene “messo a
terra”, una qualunque distribuzione di cariche fisse al suo interno non può produrre alcun effetto elettrostatico all’esterno.
Vedremo invece alla voce “Gabbia di Faraday”, nella Sezione Radiotecnica, che ciò non è valido per le cariche in moto nel conduttore o per campi elettrici o elettromagnetici variabili.
Bibliografia.
Gli esperimenti di Coulomb sono descritti in E. Bellone, Storia della fisica moderna e contemporanea, UTET, Torino 1998.
Per una chiara sintesi sia dell`importanza dell`esponente 2, sia della storia di questi esperimenti si consiglia l`articolo di A. S. Goldhaber e M. M. Nieto, La massa del fotone, Le Scienze, settembre 1976.
Le figure 5-9 e 5-10 sono state tratte da R. P. Feynman, R. B. Leighton e M. Sands, The Feynman Lectures on Physics, Vol. II, H. Addison – Wesley, P. C. Massachusetts, 1964.
La figura N 1045 è a pag. 249 del catalogo: Apparecchi per
l’Insegnamento della Fisica, a cura del prof. R. Magini, Officine Galileo, 1940.
La sfera è esposta al Museo MITI, su proposta di Fabio Panfili.
Foto di Claudio Profumieri, elaborazioni, ricerche e testo di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.

 

 

 

 

 

 

Vacuometro di Gaede. Prima parte.

Wolfgang Gaede (1878-1945)

«Strumento in vetro utilizzato per misure di vuoto (in particolare nei laboratori di chimica organica per controllare distillazioni a pressione ridotta).
Le estremità sono graduate in mm Hg (una scala più alta ed una più bassa).
Viene caricato con mercurio, e si installa orizzontalmente su un apposito sostegno che gli permette di inclinarsi di 90° verso destra o verso sinistra.
Il raccordo posteriore si collega mediante un tubo per vuoto alla camera o al recipiente da misurare.
Al momento della misura viene ruotato da un lato o dall`altro per portare in basso la scala adeguata al grado di vuoto e si effettua la lettura.
Quindi lo si riporta in posizione di riposo orizzontale affinché la pressione nel vacuometro si adegui ad eventuali variazioni del sistema da misurare, e lo strumento sia pronto per una successiva lettura».
Testo del Dott. Enrico Castelli (To), che ringrazio per le informazioni sul vacuometro che mi hanno reso possibili le ricerche. Fabio Panfili.

Note di Fabio Panfili:
1) Le due scale nel tubo a U vanno da 0 a 40 mm Hg; quella nella parte opposta è muta.
2) Nell`inventario del 1956, in data 15 giugno 1959 al n° 1690 è citato un “vacuometro” senza ulteriori indicazioni.
3) Le due pagine qui riportate sono di un antica scheda di istruzioni della E. Leybold’s Nachfolger senza data rinvenibile all’indirizzo:
http://cerere.astropa.unipa.it/biblioteca/Strumenti/frameset.htm.
Per consultare la seconda parte scrivere: “Vacuometro” su Cerca.
Foto di Claudio Profumieri e Ilaria Leoni, elaborazioni e ricerche di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.