Apparecchio per la dimostrazione dello schiacciamento polare della Terra.
Nell`inventario del 1912, si legge: “Molla d`acciaio per la dimostrazione dello schiacciamento della Terra nei suoi poli, già esistente, in buone condizioni, costo ₤ 4”; nell`inventario del 1919 è detto: “Apparecchio per dimostrare l`ellissoidità della Terra”.
Per chiarire quanto scritto nell`inventario del 1919, ricordiamo che la superficie media dei mari si chiama geoide e in prima approssimazione questo ha la forma di un ellissoide di rotazione, schiacciato ai poli. Nei dati dell`epoca il semiasse polare è di circa 6356752 m mentre quello equatoriale è di circa 6378137 m e il loro rapporto è di 0,9966.
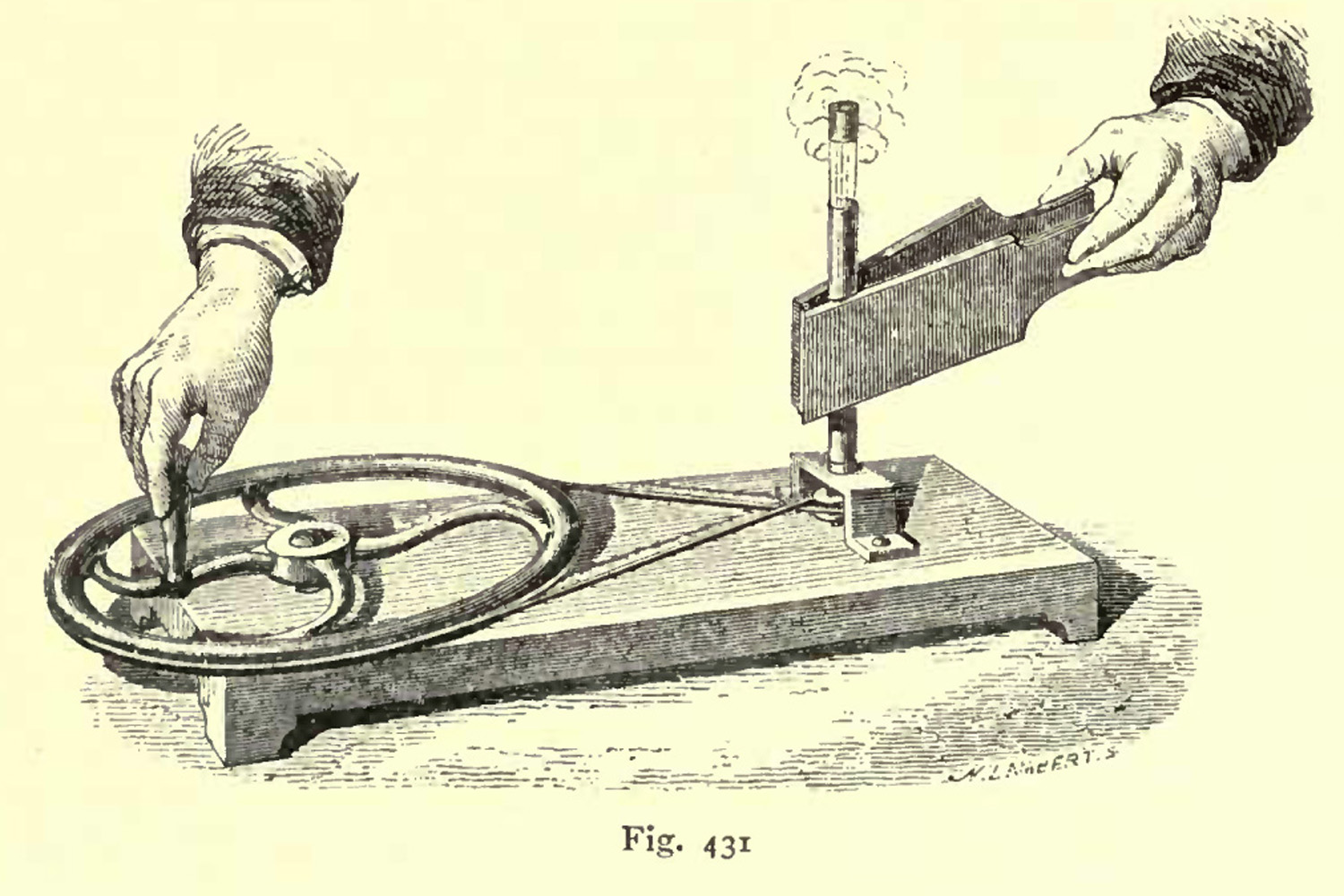
Il dispositivo è costituito da due nastri di acciaio incrociati, foggiati a cerchio, uniti sulla sommità ad un anello che può scorrere sull`alberino centrale, mentre l`anello sottostante è fisso. Il suo funzionamento è di una semplicità tale da indurre a pensare che il fenomeno da mostrare abbia una spiegazione altrettanto semplice. Vedi la figura che lo mostra in moto.
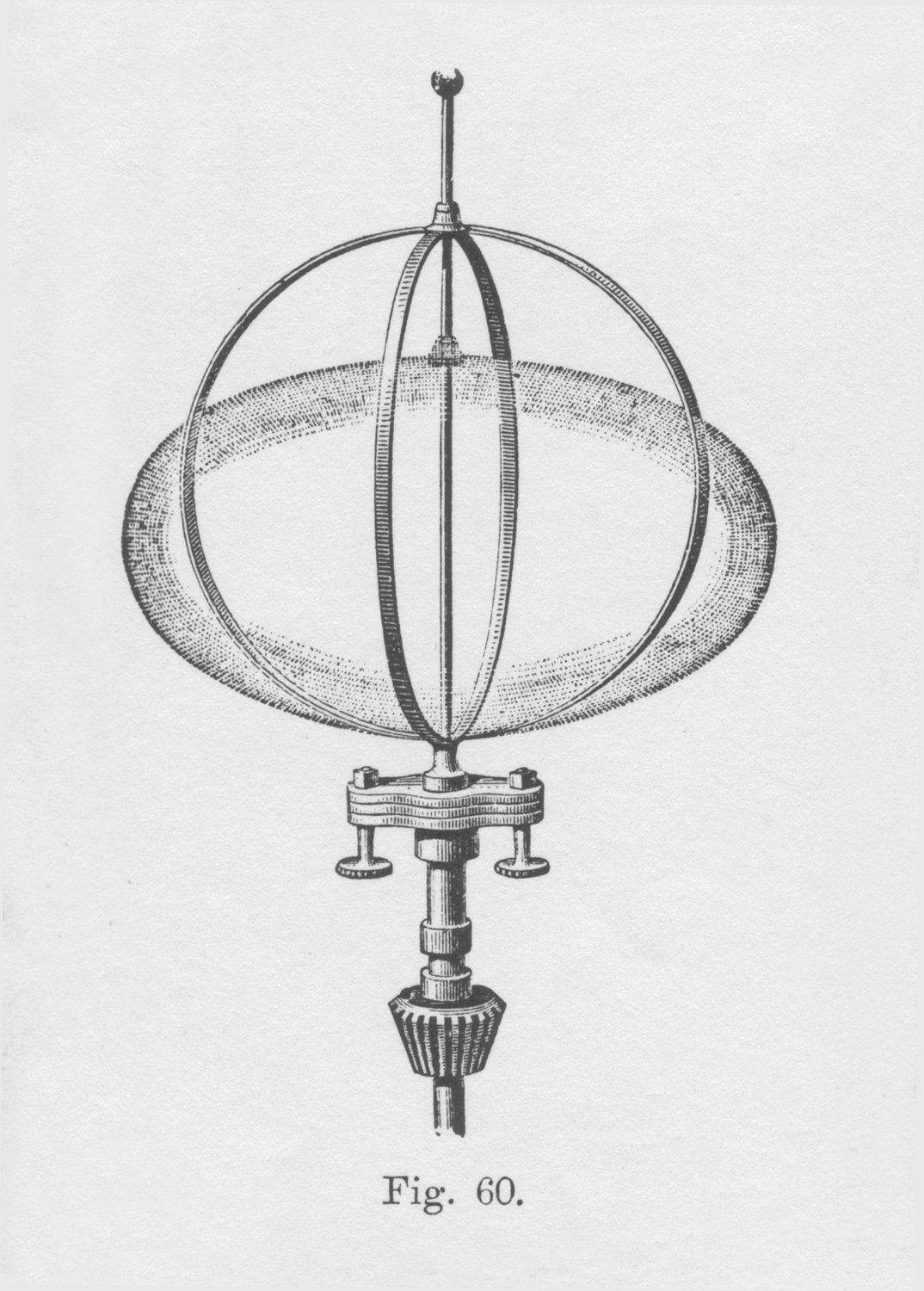
Quando il sistema è a riposo ricorda una forma sferica, ma non appena esso viene posto in rotazione si schiaccia, assumendo l`aspetto di un ellissoide la cui confusa visione è dovuta alla persistenza delle immagini sulla retina. All`aumentare della velocità di rotazione, lo schiacciamento ai poli diventa sempre più accentuato e si suole attribuire questo fenomeno alle cosiddette forze centrifughe. Dunque, per una certa velocità angolare, la forza centrifuga è direttamente proporzionale alla distanza R, quindi essa cresce in valore dai poli all`equatore, risultando massima negli elementi equatoriali dei nastri. All`aumentare della velocità angolare, la forza centrifuga aumenta notevolmente e lo schiacciamento è più evidente. Dal punto di vista dell`equilibrio nel sistema rotante, i nastri flessibili si schiacciano finché la forza elastica non è sufficiente ad equilibrare quella centrifuga.
Questa interpretazione comporta una intrigante ed intricata storia delle idee.
Per chi considera il fenomeno da un punto di vista esterno invece, i nastri si deformano finché non sono capaci di sviluppare la forza elastica centripeta necessaria a mantenere gli elementi di essi sulle loro traiettorie circolari, poiché essi tenderebbero a sfuggire lungo la tangente alla traiettoria, per inerzia.
Le forze centrifughe si dicono apparenti, nel senso che appaiono, come fantasmi, solo in sistemi in rotazione.
Per intenderci meglio, facciamo un giro in giostra. Mentre giriamo, sentiamo una forza che ci spinge verso l`esterno, diretta lungo il raggio; possiamo osservare che essa è più intensa in periferia che non vicino al centro e che agisce su tutti i corpi presenti sulla giostra, anche sugli oggetti che teniamo in tasca.
Un osservatore esterno però ci fornisce una versione molto diversa. Egli afferma che la nostra è solo una sensazione biologica e che la vera forza che ci fa ruotare è diretta verso il centro ed è dovuta ai sostegni cui siamo appoggiati. Se infatti noi lasciamo i sostegni, non veniamo proiettati verso l`esterno, ma piuttosto in avanti nel senso del moto, e contemporaneamente la forza che sentivamo scompare come per magia.
La giostra è un sistema di riferimento non inerziale, mentre il sistema in cui si trova l`osservatore si può, con una certa approssimazione, definire inerziale.
Dopo aver eseguito un famoso esperimento con un secchio ruotante, Newton affermò che esiste un sistema di riferimento assoluto e i moti descritti rispetto ad esso si dicono assoluti (Principia, 1686).
Egli ipotizza infatti l`esistenza di un «qualunque vuoto immenso ove non esiste alcunché di esterno e sensibile», ma cade in un circolo vizioso poiché introduce lo spazio assoluto per giustificare gli effetti delle forze centrifughe, e, per provare l`esistenza dello spazio assoluto, da lui stesso descritto come non osservabile, ha come unica prova il manifestarsi di quelle forze.
Bisogna però aggiungere che, nelle premesse al suo esperimento, mostra una certa perplessità: «È difficilissimo in verità conoscere i veri moti dei singoli corpi e distinguerli di fatto dagli apparenti: e ciò perché le parti dello spazio immobile, in cui i corpi veramente si muovono, non cadono sotto i sensi. La cosa tuttavia non è affatto disperata».
L`esperimento di Newton è il seguente: un secchio contenente abbastanza acqua viene fatto ruotare intorno a un asse verticale, per esempio con una corda ritorta annodata al manico e poi lasciata libera di svolgersi. La superficie dell`acqua si incurva quando il liquido ruota in assoluto e non quando ruota soltanto rispetto al secchio, cioè quando, all`inizio, il contenitore ruota e l`acqua è ancora ferma. La curvatura dipende dal campo di forze centrifughe.
Venti anni dopo la pubblicazione dei Principia, Berkeley mosse alcune critiche notevoli alle idee di Newton: 1) non ha senso parlare di spazio assoluto in quanto non è osservabile; 2) le forze centrifughe si manifestano quando c`è rotazione rispetto alle stelle fisse, mettere in relazione il moto dell`acqua rispetto al secchio non ha alcun significato, poiché questo è un mero contenitore; 3) non ha alcun senso parlare di moto di uno o due corpi in uno spazio vuoto, senza alcun riferimento.
Le stelle fisse sono quegli oggetti celesti luminosi i cui moti, relativi alla moltitudine degli altri corpi del firmamento, osservati per lunghi periodi, risultano irrilevanti. Oggi si possono identificare con le galassie lontane.
Per spiegare le ragioni di Berkeley riportiamo un esempio ormai classico illustrato da Berkeley nel De Motu e poi di nuovo usato da A. Einstein.
Vedi in proposito il nero di china del prof. arch. Giovanni Rastelli, ispirato ad uno scarno disegno di chi scrive.
Si consideri un universo fittizio costituito soltanto da due pianeti luminosi, dello stesso materiale deformabile e delle stesse dimensioni, posti ad una distanza sufficiente a rendere trascurabili gli effetti gravitazionali reciproci. Si supponga inoltre che ciascun pianeta, rispetto ad un osservatore posto sull`altro, ruoti con velocità angolare costante, intorno alla congiungente i loro centri, e che uno sia sferico e l`altro ellissoidale.
Secondo Newton, quest`ultimo è in rotazione assoluta poiché è deformato dalle forze centrifughe, mentre l`altro è in rotazione relativa al precedente.
Ma un abitante del corpo schiacciato potrebbe giungere a una conclusione opposta: «Il mio pianeta è fermo, io sento gli effetti delle forze centrifughe, vedo l`altro pianeta girare di moto rotatorio assoluto e ne deduco che lo schiacciamento del mio pianeta è dovuto al suo stato di quiete rispetto allo spazio assoluto, altrettanto posso dire delle forze centrifughe». Noi non possiamo sapere quali risultati darebbe il nostro apparecchio messo in funzione su uno dei due corpi celesti, poiché non sappiamo se in quell`universo senza galassie e stelle vale la fisica del nostro universo. Inoltre possiamo affermare, come osservatori esterni, che entrambi i corpi ruotano e che non riusciamo a spiegarci come mai essi, pur essendo posti in condizioni simili, abbiano forme così diverse. Infine ci sembra privo di fondamento, da un punto di vista strettamente fisico, che si possa attribuire allo spazio vuoto la causa di tale fenomeno. [Oggi pare che lo spazio apparentemente vuoto del nostro Universo sia “permeato” da materia ed energia oscure di cui, almeno a tutto il 2017, si hanno congetture da provare sperimentalmente.]
Nel 1872 Mach elaborò ulteriormente le affermazioni di Berkeley: «Ovviamente non ha importanza se noi pensiamo che sia la Terra a ruotare intorno al suo asse, o che essa sia ferma mentre le stelle fisse le girano intorno. Da un punto di vista geometrico, in tutti e due i casi, si tratta di un moto relativo della Terra e delle stelle fisse l`una rispetto alle altre. Ma se ammettiamo che la Terra sia ferma e che le stelle fisse le girino intorno, non c`è schiacciamento della Terra, almeno secondo la concezione che noi abbiamo della legge di inerzia. Ora possiamo superare questa difficoltà in due modi: o ogni moto è assoluto, o la nostra legge di inerzia è formulata in modo sbagliato. Io preferisco la seconda soluzione. La legge di inerzia deve essere concepita in modo da portare allo stesso risultato sia nella prima che nella seconda ipotesi. È perciò evidente che nella sua formulazione bisogna tener presenti le masse dell`Universo». Secondo Mach in definitiva le forze centrifughe dipendono da tutte le masse dell`universo, anche le più lontane.
Einstein, in una nota del 1912, chiamò tutto ciò: “Principio di Mach”.
Bisogna pur dire che, nell`enunciare il suo Principio, a Mach era sfuggita l`importanza della relazione tra massa inerziale e gravitazionale. Del resto anche Newton la riteneva una mera coincidenza.
Einstein era affascinato dalle idee di Mach e cercò di includerle nella sua Teoria della Relatività Generale (1916) ma, introducendo l`eguaglianza tra massa inerziale e gravitazionale, ne derivò che le forze di inerzia, come quelle centrifughe appunto, sono equivalenti a forze gravitazionali e con ciò perdono il loro carattere evanescente acquistando una realtà fisica.
Questi concetti sono molto diversi da quelli espressi da Mach.
Proviamo a riassumere quanto esposto: 1°) Newton ritiene che le forze centrifughe sono forze di inerzia dovute alla rotazione rispetto allo spazio assoluto. 2°) Secondo Berkeley e Mach quelle forze appaiono quando la rotazione avviene rispetto alle stelle fisse, che dunque formano un sistema di riferimento privilegiato. 3°) Einstein afferma che non esistono sistemi di riferimento assoluti o privilegiati, ma che i sistemi accelerati, almeno localmente, sono equivalenti ai campi gravitazionali.
Per spiegare quest`ultima frase riportiamo un esempio classico dovuto allo stesso Einstein. Un osservatore si trova in uno strano ascensore, fornito di un finestrino inizialmente chiuso, posto in una regione dello spazio lontanissima da corpi celesti. Egli si sente a suo agio e, salendo su una comune bilancia, vede che il suo peso ha il solito valore; dunque è convinto di trovarsi sulla Terra o quanto meno su un luogo simile. Ma improvvisamente si apre il finestrino e con stupore si accorge che silenziosamente un motore sta tirando le funi dell`ascensore e che questo accelera con la stessa intensità dell`accelerazione gravitazionale alla superficie della Terra. Ciò comporta la sensazione di peso e la distinzione tra l`alto e il basso. Da qui l`indistinguibilità tra gli effetti inerziali e gravitazionali.
Ecco dunque che una innocente rotazione di un semplice apparecchio mostra una deformazione la cui causa, ancora oggi, non è facile spiegare.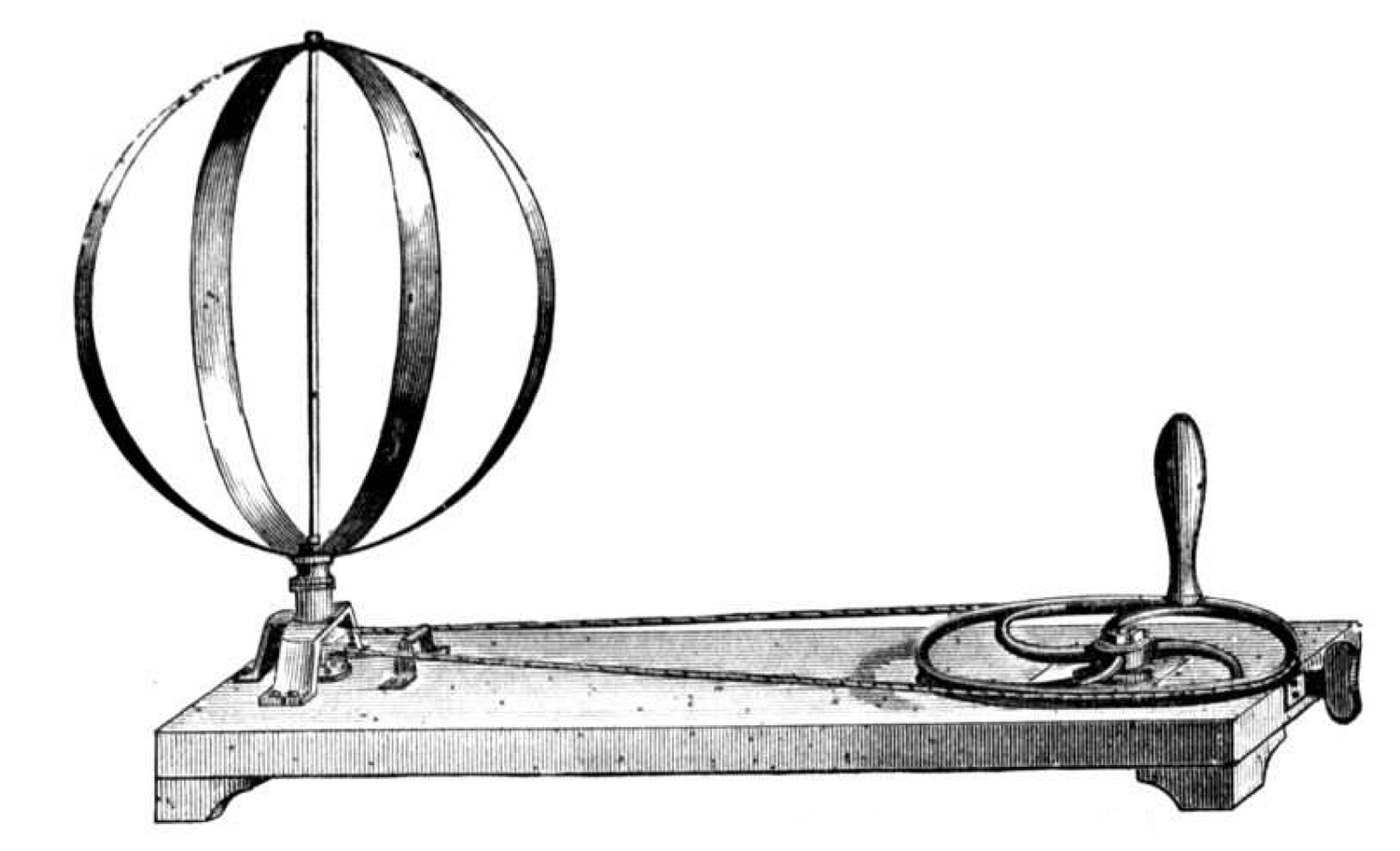
La figura con l`intero dispositivo è a pag. 8 del Priced and Illustrated Catalogue of Physical Instruments. J. W Queen & Co. Philadelphia 1884. Rinvenibile all’indirizzo:
https://www.sil.si.edu/DigitalCollections/trade-literature/scientific-instruments/files/52503/
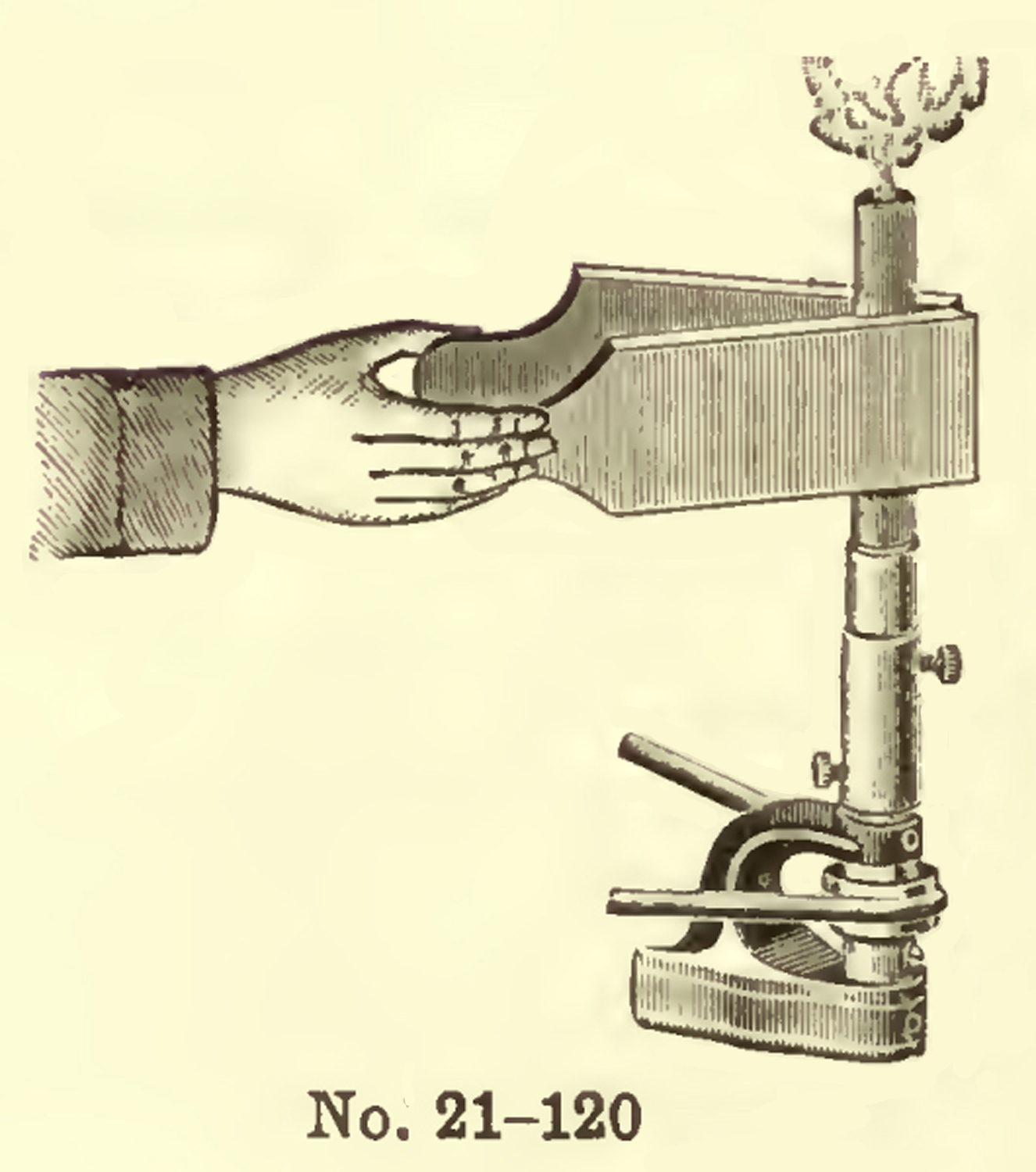
La figura B 285 è a pag. 28 di Apparecchi per l’Insegnamento della Fisica a cura del prof. R. Magini, Officine Galileo, 1940.
Bibliografia.
M. Ceccarelli, Una betulla per la Pio, appunti per insegnare la fisica (o per tentare di dimenticarla), Zanichelli Bologna 1968.
A. Funaro e R. Pitoni, Corso di fisica e chimica, R. Giusti Livorno 1907, da cui è tratta la figura 60 di pag. 59.
L. Segalin, Fisica sperimentale, vol. I, G. B. Paravia & C., Torino 1933.
A. Einstein, La relatività, Newton Compton, Roma 1970.
A. Einstein e L. Infeld, L`evoluzione della fisica, Boringhieri, Torino 1965.
A. Einstein, I fondamenti della relatività, Newton Compton, Roma 1976.
W. Bonnor, Universo in espansione, Boringhieri, Torino 1967.
M. Born, La sintesi einsteiniana, Boringhieri, Torino 1959.
D. W. Sciama, La sintesi dell`Universo, Einaudi, 1965.
L. Gratton, Relatività cosmologia astrofisica, Boringhieri, Torino 1968.
V. de Sabbata, Seminari di un corso di aggiornamento su questioni di base in cosmologia, La Fisica nella Scuola, XXVI, 3IR, Q3, 1993.
E. Gasco, Il Principio di Mach: le prime considerazioni di Einstein (1907-12), Quaderni di Storia della Fisica, n° 13, Giornale di Fisica S.I.F., Bologna 2005.
F. Panfili, Il Girotondo, un secchio, Newton, Berkeley, Mach, Einstein e altri, Il Montani, n°1, Fermo 1984.
Foto di Federico Balilli, nero di china di Giovanni Rastelli, elaborazioni, ricerche e testo di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.
Tubo sonoro a pistone con imboccatura a flauto.
