Categoria: fisica

Proiettore cinematografico sonoro 16 mm Cintia Dominator, mod. S, N° 01108. Seconda parte.
Costruito in Italia dalla S.p.A. Cinelabor – Firenze. Come si legge su una targhetta.
Nell`inventario D del 1933/1937, al n° 1316 in data 20 giugno 1951 si legge: “Soc. Cinelabor – Firenze. Cineproiettore mod. Dominator 15″ sonoro a passo ridotto, completo di autotrasformatore per le varianti di tensione di alimentazione. ₤ 400.000”.
Esso è stato rinvenuto  dall`Ing. Claudio Profumieri e dal Prof. Fabio Panfili; l`Ing. Profumieri con la consueta perizia e meticolosità ha provveduto a smontarlo e ripulirlo in ogni sua parte rendendolo di nuovo efficiente.
Per ora manca il sonoro poiché la fotocellula non funziona; si pensa di sostituirla in seguito con una identica.
In queste foto sono ben visibili i tre tamburi a 12 denti per il trascinamento, poco visibile invece una griffa a tre denti lavorante in un pattino curvo a pressione laterale.
Per consultare le altre sei parti scrivere “Dominator” su Cerca.
Elaborazioni e ricerche su inventari di Fabio Panfili. Restauro, foto e testo di Claudio Profumieri.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.

 

 

 

 

 

 

 

Piccolo rocchetto di Ruhmkorff a flusso variabile.
Costruito dalla Phywe, è anteriore al 1968.
Sullo chassis del secondario reca le seguenti scritte: Phywe 06517.00; Made in Germany ; 1200Wdg ; max 0,08 A 2 KΩ 4 H.
Il condensatore di 0,4 µF è posto in parallelo al contatto del martelletto per attenuare la scintilla dovuta alla f.e.m. di autoinduzione che si manifesta all`apertura del circuito.
La valenza didattica di questo rocchetto è dovuta alla possibilità di variare l`accoppiamento tra primario e secondario, per mostrare che quando i due avvolgimenti sono sovrapposti l`efficienza della macchina è massima; inoltre permette di far osservare agli allievi sia il primario sia il secondario separati.
Per avere notizie sul suo funzionamento si fa riferimento sia alla scheda sui due rocchetti più antichi e di grandi dimensioni, sia alle due schede relative ad un antico rocchetto a flusso variabile; tutte rinvenibili nella voce dedicata all`Elettrotecnica.
L’ultima foto mostra questo esemplare vicino ad un bellissimo rocchetto della Leybold Didactic GHDH, che come dimensioni è il terzo della collezione del Montani.
Foto di Claudio Profumieri, elaborazioni, ricerche e testo di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.

 

 

 

 

Pinzetta a due tormaline per la polarizzazione della luce.Non rinvenibile negli inventari dell`epoca e di difficile datazione, anteriore comunque al 1950.
Nel 1816 J. P. Biot scoprì le proprietà della tormalina e in seguito costruì la pinzetta.
Le due piastrine circolari, tagliate da un cristallo di tormalina parallelamente all`asse ottico, sono fissate su supporti girevoli alle due estremità della pinza.
Esse servono per visualizzare in modo qualitativo la polarizzazione della luce.
La tormalina è un cristallo birifrangente dicroico di vari colori; questo esemplare è di color marrone scuro.
Quando la luce ordinaria non polarizzata entra in una lastrina, che funge da polarizzatore, subisce una doppia rifrazione. Il dicroismo fa si che il raggio ordinario venga assorbito dalla lastrina, se non è troppo sottile, mentre quello straordinario la attraversa passando all`altra tormalina che diventa l`analizzatore.
L`occhio viene posto dopo l`analizzatore e, ruotando una delle due lastrine, si passa gradatamente dal campo visivo luminoso al campo scuro.
Quando gli assi delle tormaline sono paralleli si ha passaggio di luce, mentre quando sono perpendicolari si ha l`assorbimento da parte dell`analizzatore e quindi un campo visivo scuro.
Se si scambiano i ruoli delle tormaline, il fenomeno resta identico.
L`impiego più interessante consiste nel porre tra le due tormaline lamine ritardatrici a quarto d`onda o a mezz`onda, cristalli sottili trasparenti di varia natura o, più banalmente, dello scotch per osservare altre proprietà della luce e della materia con effetti cromatici suggestivi. Tutto ciò si ottiene ruotando in modo opportuno le tormaline.
Bibliografia:
F. Cajori, Storia della Fisica Elementare, Zanichelli, Bologna 1908.
Il disegno che illustra la proprietà del cristallo dicroico è tratto da F.  W. Searse, Ottica, C. E. Ambrosiana, Milano 1982.
Il disegno sull`uso delle due tormaline è tratto da P. Caldirola – G. Casati – F. Tealdi, Fisica 1, Ghisetti & Corvi, Milano 1987 ed è anche rinvenibile in D. Halliday – R. Resnick, Fisica 2, CEDAM, Milano 1982.

Foto di Claudio Profumieri, elaborazioni, ricerche e testo di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.

 

 

 

 

Piramide  tronca a base triangolare per illusione ottica.
Nell’inventario del 1912 al N° 895 si legge: “Prisma a riflessione totale sagomato, già esistente, in condizioni cattive, costo ₤ 1”.
Invece non ci sono elementi sufficienti per identificare questo esemplare con la descrizione di un “prisma a riflessione totale” citato come già esistente nell’inventario del 1906 e che potrebbe riferirsi proprio ad un prisma.
Vista di fronte da l’illusione di osservare una colonna di cristallo. Vista di lato rivela il profilo ottenuto con un preciso lavoro di molatura e lucidatura sul vetro.
L’illusione si basa sul fenomeno della riflessione interna totale.
Non si hanno notizie sul fabbricante.
Alcune foto mostrano sullo sfondo la suggestiva galassia a spirale M51 detta Whirlpool, su idea dell’ing. Claudio Profumieri.
Altre foto sono dovute a un gioco di elaborazioni di Fabio Panfili.
Il manifesto è stato ideato e realizzato da Massimo Ciccola in occasione del 6° premio Mario Guidone; chi scrive tenne una conferenza sulla “Complessità della riflessione ottica” con riferimenti teorico-sperimentali a fenomeni di riflessione, interferenza e diffrazione in ottica, acustica e nel campo delle microonde, accennando sia alle spiegazioni classiche sia all’interpretazione secondo l’elettrodinamica quantistica.
Federico Balilli nell’occasione diede la sua competente collaborazione.
L’oggetto è esposto al Museo MITI, su proposta di Fabio Panfili.
Foto di Claudio Profumieri, elaborazioni, ricerche e testo di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.

 

 

 

 

 

 

 

 

 

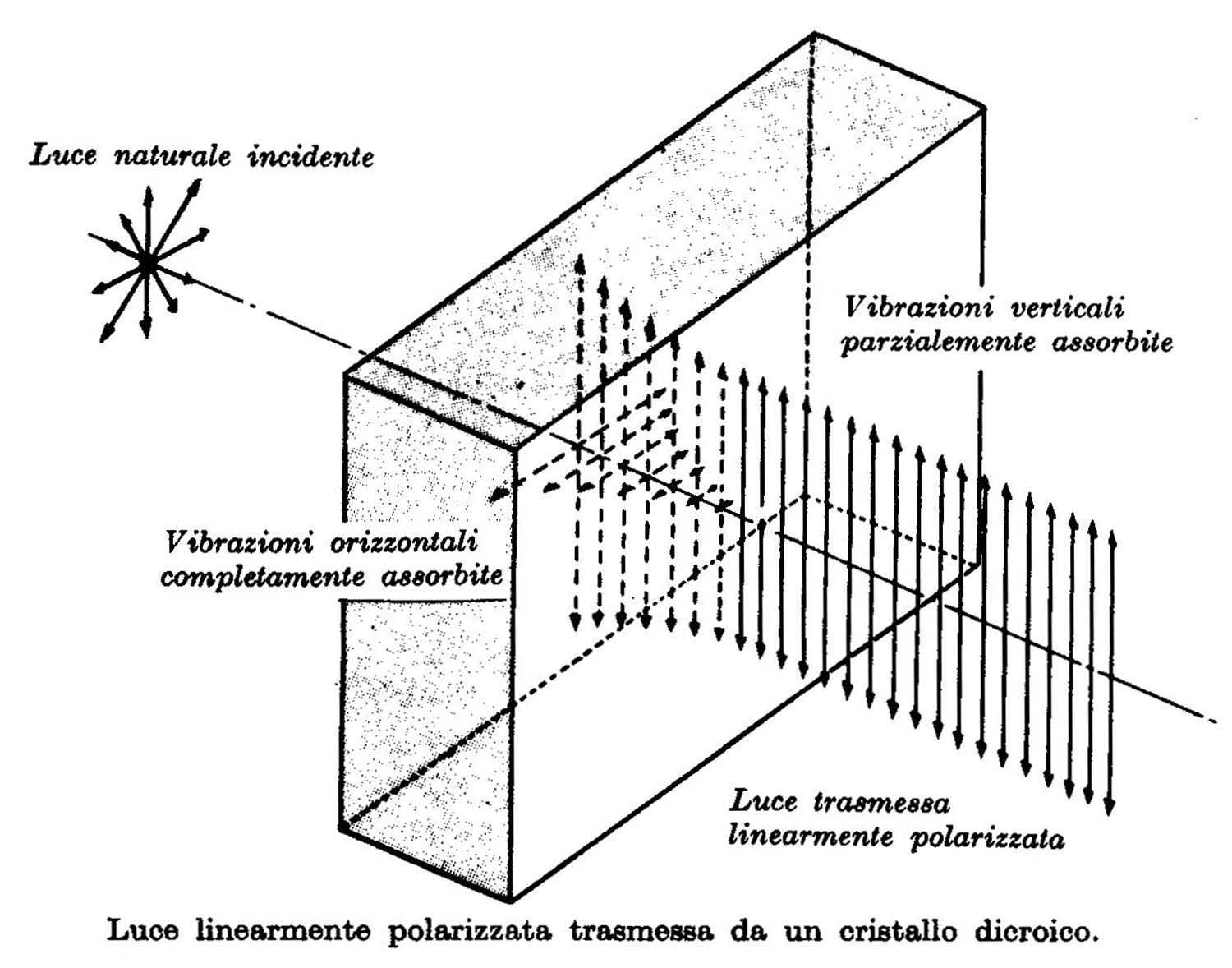
Pista centrifuga.
Inventario D del 1956 n° 1744.
La pista centrifuga mostra essenzialmente che se il cilindretto parte da una posizione della discesa, inferiore a quella corrispondente ad una ben definita altezza minima rispetto alla base, non riuscirà a completare il giro, cadendo nel primo tratto del cerchio.
L`altezza minima si determina per via sperimentale.
Il cilindretto ha i bordi sagomati in modo tale da non farlo uscire dalla pista durante la discesa.
Le foto con stroboflash sono state realizzate da Federico Balilli, coadiuvato da Angelo Sgammini, con una macchina fotografica tradizionale e pellicola in bianconero.

Per rendere stimolante una lezione di fisica sulla conservazione dell`energia meccanica, dapprima si fa osservare l`apparecchio in funzione, poi si invitano gli allievi a fare una previsione approssimata di quella altezza minima. Si suggerisce quindi che, per risolvere il problema, essi possono applicare il suddetto principio di conservazione, unitamente a una particolare equazione che normalmente si usa nel problema dei satelliti in orbita circolare.
 Le considerazioni che seguiranno sono valide  solo se il cilindretto, fin dall’inizio del suo moto, rotola senza scivolare.
Altrimenti è necessario ricorrere al principio generale della conservazione dell’energia e ciò esula dall’intento di queste note.
Nella pratica sperimentale infatti la pendenza della discesa causa un evidente scivolamento iniziale del cilindretto, a cui segue il rotolamento, ciò comporterebbe una difficile trattazione teorica.

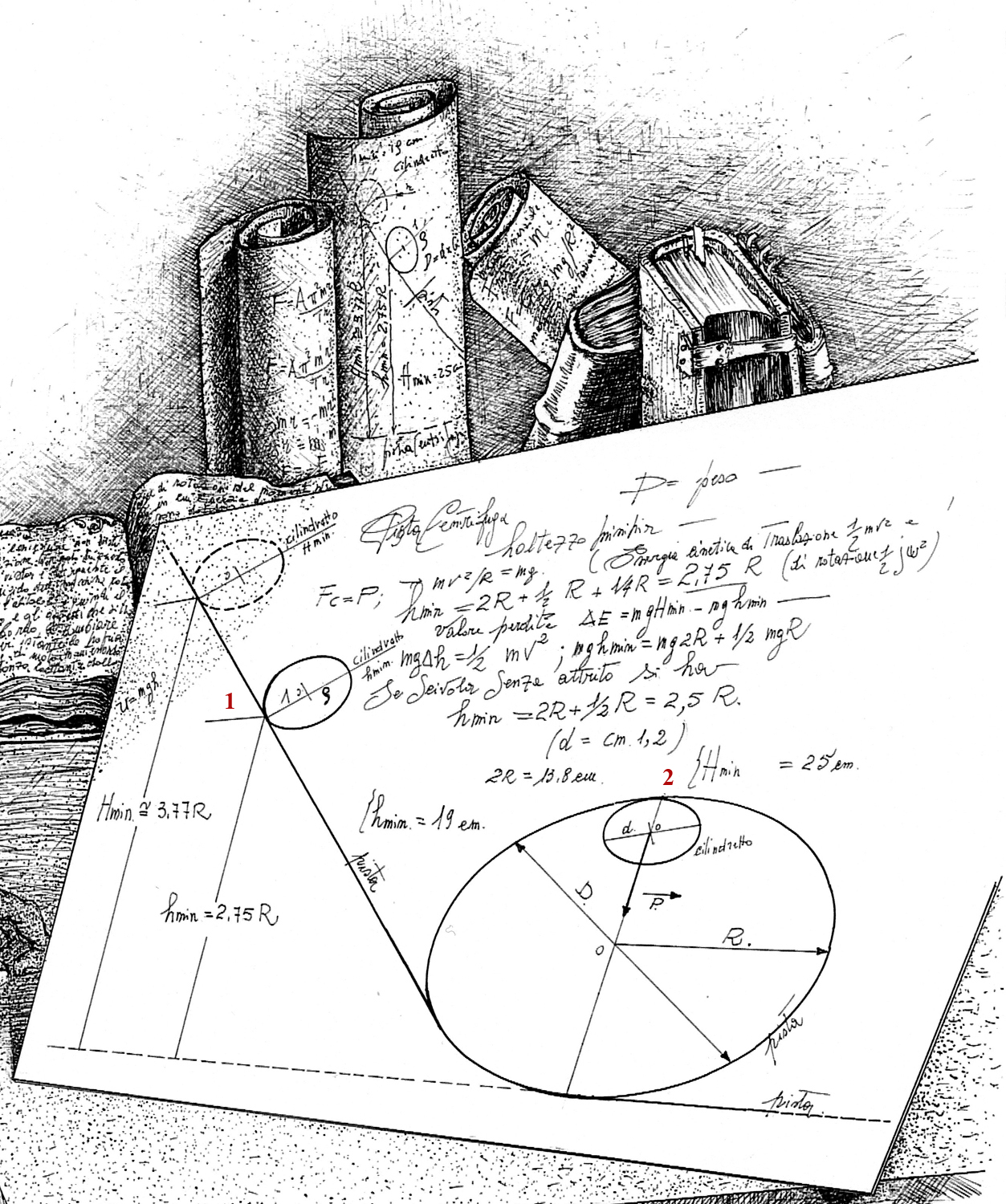
 Quando il cilindretto è posto ad una certa altezza rispetto al piano di appoggio (posizione 1 nel disegno in nero di china), il sistema cilindretto – Terra possiede una energia gravitazionale locale: U = mgh. Non appena viene lasciato libero il cilindretto rotola giù.
Se si trascurano le perdite dovute agli impedimenti, così li avrebbe chiamati Galileo, si può affermare che l’energia potenziale iniziale si è trasformata, al punto 2 nel disegno, in energia cinetica di traslazione ½ mv²  e di rotazione ½Jω² , pur restando una residua energia potenziale di mg2R:
mgh = mg2R + ½ mv²  + ½ Jω²       (A) .
Si trova inoltre che il cilindretto raggiunge agevolmente il punto 2 nel disegno se si verifica la condizione che la forza centripeta  in quel punto è dovuta solo al peso P; si scrive dunque:
F_c = P        (B)
e cioè
mv² / R = mg
dove R è il raggio del cerchio formato dalla pista in quel tratto.
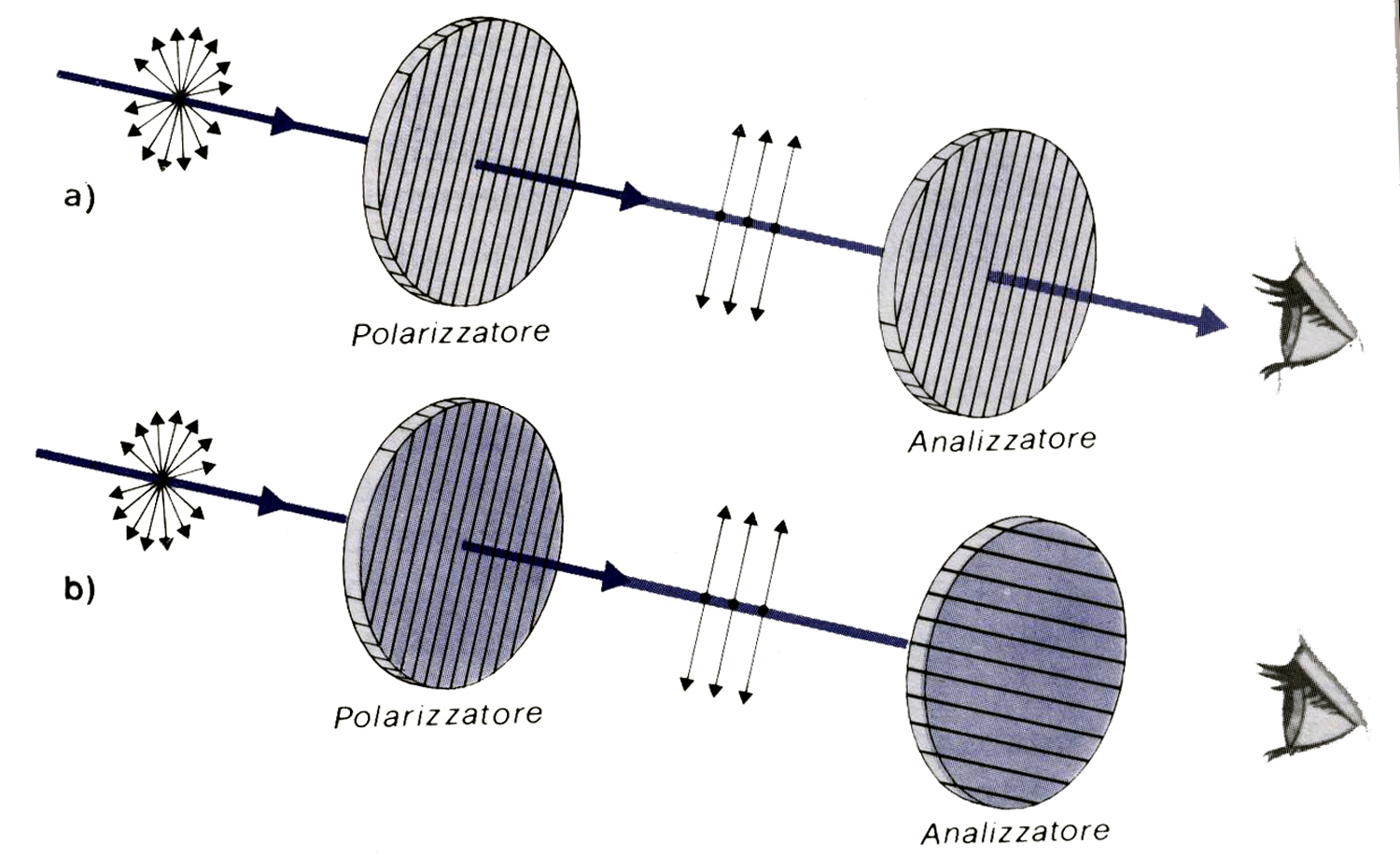
Questa condizione fornisce il limite minimo del valore della velocità al punto 2. Infatti se il cilindretto avrà una velocità inferiore, cadrà prima del punto 2 senza completare il giro, poiché il peso ne curverà eccessivamente la traiettoria, come si osserva nella prima foto qui sotto.
Mentre per velocità superiori, la forza di sostegno della pista si sommerà al peso, per dare la forza centripeta verso il basso, e il cilindretto proseguirà nella sua corsa, come nella foto successiva.
 Dalla (B)  si ha:
v² = gR    (C)
Tenendo inoltre presente che ω²  = v²/r², si ottiene:
ω²  = gR/r²  (D)
dove r è il raggio del cilindretto.
Sostituendo la (C) e la (D) nella (A) si ottiene:
mgh_min = mg2R + ½ mgR + ½ JgR/r²
per il cilindretto, il momento di inerzia J = mr², dunque, sostituendo e semplificando opportunamente si ottiene:
h_min = 2R + ½ R +¼ R = 2,75 R
Fatta la previsione si passa all’esperimento che mostra subito la consistenza delle perdite di energia durante il tragitto, poiché l’altezza minima H_min richiesta per completare il giro è più grande della stima teorica h_min. La differenza
ΔE = mg H_min – mg h_min
fornisce infatti il valore di tali perdite.
Nella pratica sperimentale con questo esemplare, il valore di 2R è pari a  circa 13,8 cm, i calcoli per la previsione teorica danno per h_min poco meno di  19 cm, mentre il valore sperimentale è H_min = 26 cm circa.
Ci si può chiedere ora che cosa accadrebbe se il cilindretto scivolasse senza attrito. In questo caso ideale, ammesso che siano ininfluenti le resistenze dell’aria ed eventuali perdite di energia per fenomeni elettromagnetici e quant’altro, si potrebbe scrivere:
mgh = mg2R + ½ mv²     (E)
sostituendo la (C) nella (E), si ottiene:
mg h_min = mg2R + ½ mgR
da cui semplificando si ha:
h_min = 2R + ½ R = 2,5 R.
Questo valore è leggermente inferiore a quello ottenuto nel caso precedente di rotolamento del cilindretto e vale circa 17 cm.
Il disegno è un particolare di un nero di china del prof. arch. Giovanni Rastelli, dove si osserva una parte dei calcoli semplificati da proporre nello svolgimento della lezione. I numeri 1 e 2 in rosso sono stati aggiunti da chi scrive perché usati nel testo.
Qui sotto si vede il disegno completo.
Foto di Federico Balilli, elaborazioni, ricerche e testo di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.