Categoria: fisica

  Modello di cannocchiale di Porro Off. Galileo Firenze.Nell`inventario D del 1956 è registrato in data 23-08-1972; al n° 6189 si legge: “Modello di cannocchiale di Porro”.
Il cannocchiale di Porro usa due prismi per avere, con una lunghezza ridotta, forti ingrandimenti e campo visivo esteso, conservando comunque una grande distanza focale.   Come si vede nelle foto questo modello non usa i due prismi caratteristici del cannocchiale di Porro, ma due specchi piani posti ad angolo retto che svolgono lo stesso compito, risultando didatticamente solo apparentemente più semplici. Infatti per spiegare che tale configurazione scambia il basso con l`alto e la destra con la sinistra, correggendo le immagini fornite dalle lenti dell`obiettivo, non occorre premettere che con un prisma si può ottenere la riflessione interna totale e che per tale ragione Porro ideò il suo cannocchiale usando due prismi.
Ma questa scelta didattica è sostanzialmente ingenua in quanto da per scontato che l`allievo sappia già il perché uno specchio “specchia”, come se la consuetudine dia la conoscenza.
Dunque la riflessione interna totale non è più difficile da spiegare, è solo più nascosta all`attenzione comune.
Con ciò si vuol dire che i fenomeni che cadono giornalmente sotto i nostri sensi possono essere molto complessi: sia la riflessione dovuta ad uno specchio, sia la riflessione interna totale in un prisma sono appunto fenomeni complessi.
Come si vede nelle foto, l`oculare è costituito da due lenti convergenti poste su una slitta per la messa a fuoco, mentre per obiettivo c`è una lente fissa convergente.
Per l`osservazione oggettiva, si poneva una lampada ad incandescenza ad opportuna distanza dall`obiettivo e si raccoglieva l`immagine reale del filamento a fuoco su uno schermo traslucido, posto vicino alla coppia di specchi prima dell`oculare.
Per l`osservazione soggettiva si usava una seconda lente convergente come oculare composto e si osservava un oggetto lontano posto in direzione dell`asse ottico dell`obiettivo. L`oggetto veniva osservato diritto e ingrandito, ma con molte imperfezioni visive dovute principalmente all`argentatura degli specchi che è posteriore al vetro di supporto e provoca riflessioni multiple.
Nelle foto sono state messe molte altre lenti, che non sono a corredo di questo strumento, per rendere le immagini più suggestive.


La figura L 891 si trova a pag. 203 del catalogo: Apparecchi per l’Insegnamento della Fisica a cura del prof. R. Magini, Officine Galileo, 1940.
Foto di Claudio Profumieri, elaborazioni, ricerche e testo di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.

 

 

 

Modello di cuneo, Officine Galileo Firenze. Matricola N° 94092.
Nell`inventario generale n° 6 del 1925 a pag. 68, n° 2226/125, si legge: “Officine Galileo Firenze. Apparecchio per la teoria del cuneo. ₤ 131”.
Nell`inventario del 1926, al n° 644-2226 si legge: “Officine Galileo-Firenze. Apparecchio per la teoria del cuneo. ₤ 131”.
Un prisma a sezione triangolare viene forzato tra due rulli ad assi di rotazione paralleli e tende ad allontanarli. Sul piatto mobile, unito al rullo superiore, si applica la resistenza ponendovi un peso, mentre la forza motrice viene applicata al prisma con uno spago, una puleggia e un piattello su cui mettere un peso.
Tutto ciò è ben chiaro nel disegno tratto da un catalogo del 1957 della ditta costruttrice.L`esperienza è semplice: si pone l`apparecchio vicino all’orlo di un tavolo, così che il piattello possa scendere liberamente. Quindi si fa equilibrio al cuneo, che tende a retrocedere verso la parete, con una tara sul piattello. Si appoggia un peso noto sul piatto sovrastante il rullo superiore, poi, per impedire che il cuneo retroceda di nuovo, si mettono sul piattello pesi tarati che rappresentano la forza motrice.
Tutti i perni vanno leggermente oliati.
La condizione di equilibrio è: P : R = t : s ; dove P è la forza motrice, R è la forza resistente, t è lunghezza della testa e s la lunghezza del fianco.
La seconda foto mostra che abbiamo forzato il cuneo tra i due rulli per allontanarli dalla posizione di riposo senza ricorrere al piccolo peso, ma semplicemente spingendo l’asticella, che termina sulla testa del cuneo, verso la carrucola. Questo solo al fine di far vedere il cuneo che solleva il piatto sovrastante, anch’esso privo del secondo peso.


La figura B 245 si trova a pag. 12 del catalogo: Apparecchi per l’Insegnamento della Fisica a cura del prof. R. Magini, Officine Galileo, 1940.

La figura 732 è tratta dal Catalogue des Appareils pour l’Enseignement de la Physique construits par E. Leybold’s Nachfolger Cologne (1905?), che si trova all’indirizzo:
http://cnum.cnam.fr/PDF/cnum_M9915_1.pdf ;
dove a pag. 86 si legge: “*732. Dispositif servant à expliquer le fonctionnement d’un coin, daprès Frick. Trois coins d’angles différente, filet carré. Francs 53”.
La prima foto è di Daniele Maiani.
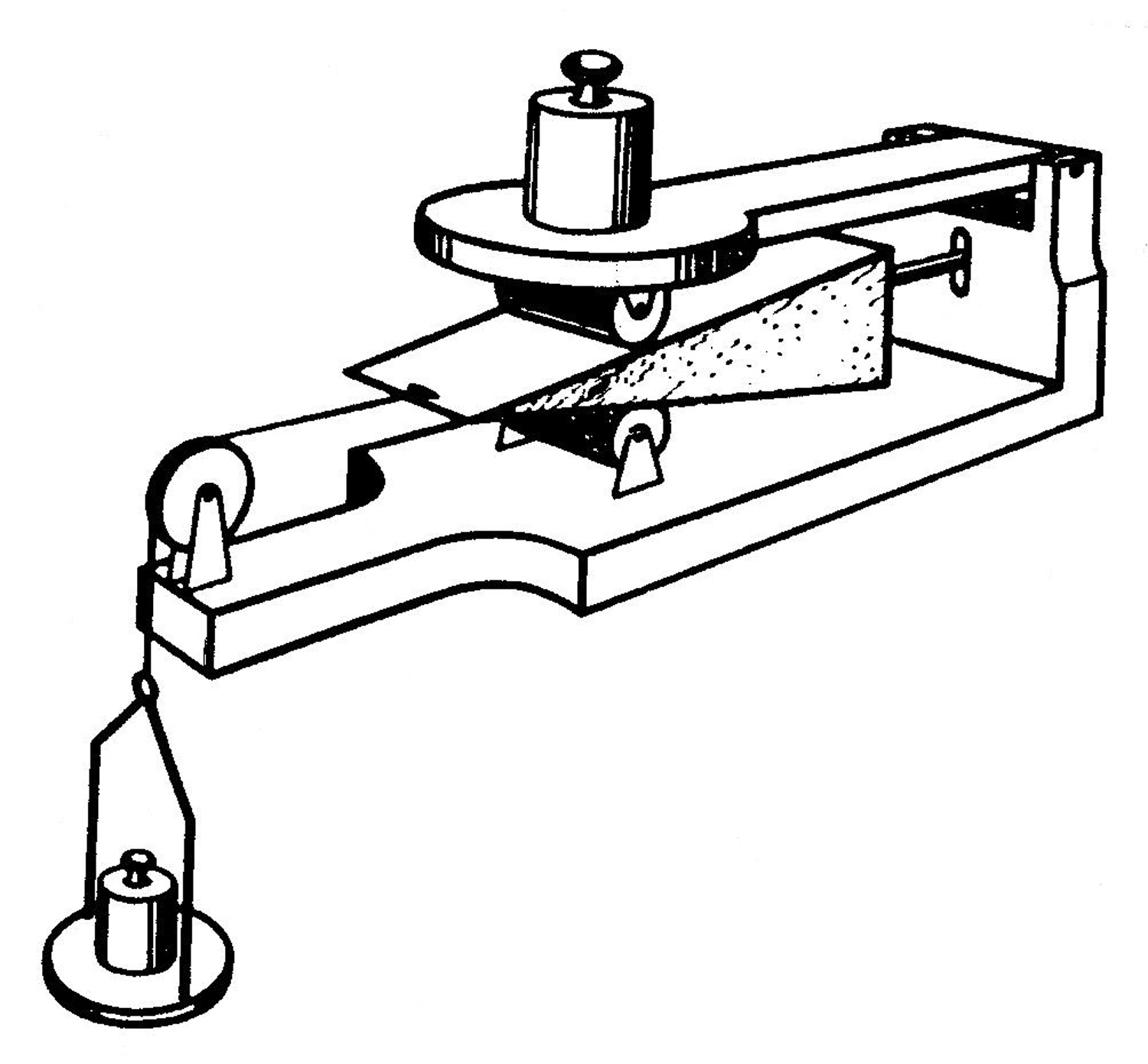
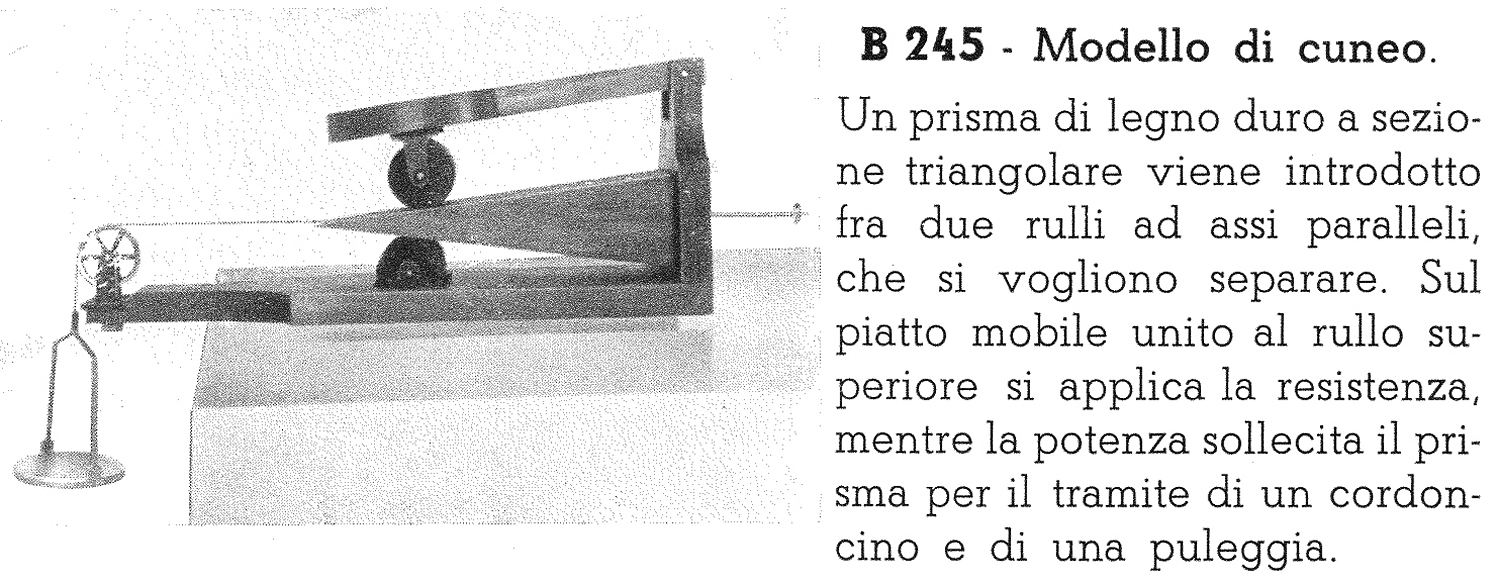
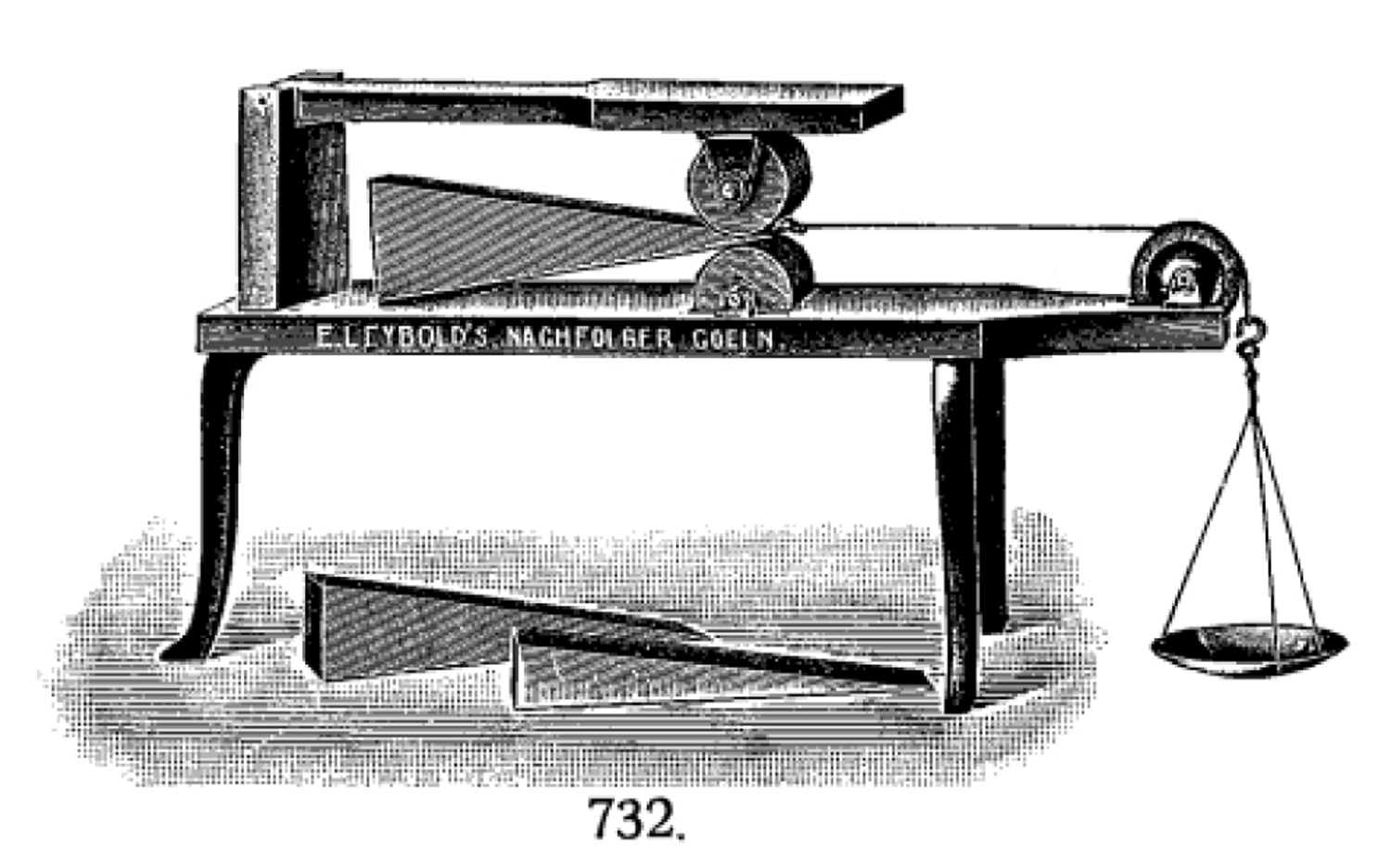
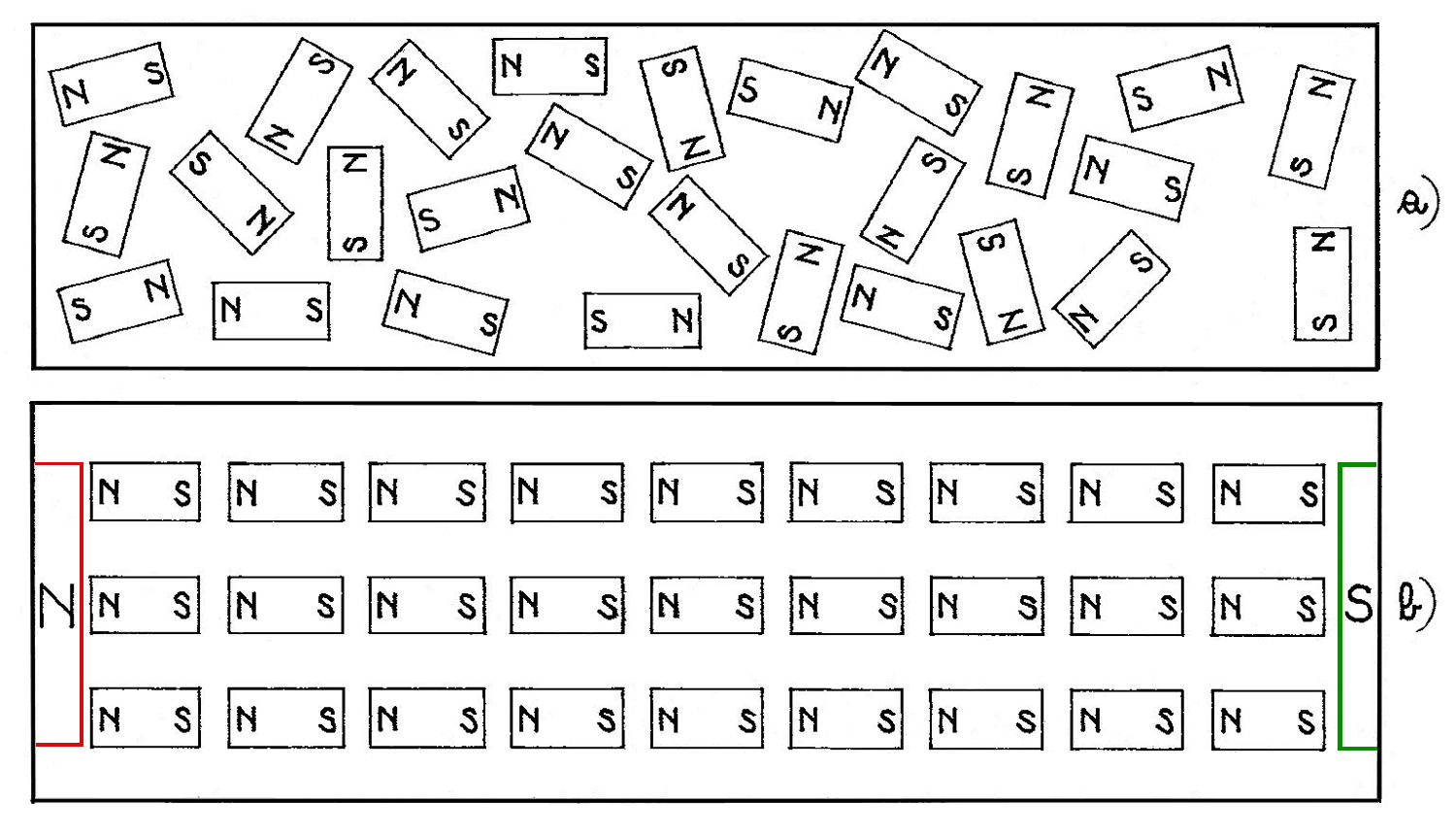
Foto di Claudio Profumieri, elaborazioni, ricerche e testo di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.   

 

 

 

 

 

 

 

 

 

 

   Modello molecolare di magnete (ovvero dei domini di Weiss).
  Inventario D del 1937 n° 368.
 Il più semplice modello idoneo a giustificare alcune proprietà del ferromagnetismo è basato sull`ipotesi che i corpi soggetti ad essere magnetizzati siano costituiti da un insieme di piccoli magneti.
Se il corpo non è magnetizzato significa che i magnetini sono orientati disordinatamente, dando luogo ad un effetto complessivo nullo; se invece esso è sottoposto ad un campo magnetico esterno, i magnetini si orientano nello stesso verso in lunghe catene il cui risultato è la magnetizzazione del corpo stesso.
L`esemplare qui descritto è costituito da una cornice di legno che regge una lastrina trasparente (forse di celluloide).
Su di essa sono fissati alcuni aghetti di acciaio su cui possono ruotare altrettanti magnetini colorati in verde e rosso per visualizzarne le polarità.
Per eseguire la breve dimostrazione dapprima si provoca manualmente un certo disordine nell`orientamento dei magnetini che, per attrazioni e repulsioni mutue, formano comunque dei gruppi orientati; poi si avvicina al dispositivo il polo di una lunga calamita e si nota il costituirsi di un ordine collettivo.
Il procedimento può essere proiettato con una lavagna luminosa.
Storicamente il primo ricercatore ad ipotizzare che il magnetismo, che si osserva nei magneti cosiddetti permanenti, fosse dovuto a minuscole correnti elettriche circolanti all`interno delle molecole fu A. M. Ampère nel 1820 circa.
Ma il suo modello, pur se ben congegnato, incontrò molte difficoltà nello spiegare i molteplici aspetti del magnetismo.

Nel 1907 P. E. Weiss sostituì questo modello con l`ipotesi, tutt`ora ritenuta valida, che entro il materiale esistano delle zone microscopiche, dette domini di Weiss, in cui i dipoli atomici sono rigidamente paralleli ed equiversi (vedi figura sopra).
Mentre in un materiale non magnetizzato questi domini sono orientati a caso, nello stesso materiale, sottoposto ad un campo magnetico esterno, si hanno sostanzialmente due effetti: a) i domini già orientati come il campo aumentano le loro dimensioni coinvolgendo quelli vicini; b) all`interno di un dominio tutti i dipoli atomici si orientano nel verso del campo esterno. Questi effetti provocano dunque la magnetizzazione del materiale.
Quindi la validità didattica di questo dispositivo sperimentale resta intatta.
La figura 80-150 è a pag. 389 di A Catalogue of Physical Instruments catalogue 17 L. E. Knott Apparatus Company Boston 1912; rinvenibile all’indirizzo:
https://archive.org/details/catalogofphyinst00knotrich?q=Catalogue+of+Physical+Instruments .
A pag. 159 del Catalogue of Physical Apparatus  E. Leybold’s Nachfolger Cologne [1910?]; rinvenibile all’indirizzo:
https://www.sil.si.edu/DigitalCollections/trade-literature/scientific-instruments/files/52546/, si attribuisce l`invenzione del dispositivo a W. von Beetz , e il costo era di $ 5,00.
La figura dei domini di Weiss è all’indirizzo:
https://it.wikipedia.org/wiki/Dominio_magnetico

Bibliografia: L. Pearce Williams, André- Marie Ampère, Le Scienze, Marzo 1989.
E. Ravagli – R. Cerruti Sola, Fisica Applicata, Vol. II, Calderini, Bologna 1983da cui è tratta la figura con le situazioni a) e b) .
D. Halliday – R. Resnick, Fisica 2, CEDAM, Milano 1982.
M. Fazio – M. Montano, Una Fisica Nuova 2, Morano, Napoli 1984.
P. Caldirola – G. Casati – F. Tealdi, Fisica 2, Ghisetti e Corvi, Milano 1987.
L`oggetto è esposto al Museo MITI, su proposta di Fabio Panfili.
Foto di Claudio Profumieri, elaborazioni, ricerche e testo di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.

                  Modello di regolatore di Watt.
 Nell`inventario del 1912 al n° 853 di pag. 49 si legge:  “Regolatore a forza centrifuga di Watt”.
 J. Watt (1736 – 1819) inventò questo “governor” intorno al 1788 forse su suggerimento di M. Boulton.
 Il regolatore di Watt serviva a mantenere costante il numero di giri della macchina a vapore agendo sul flusso del vapore.
 Quando il numero di giri della macchina scendeva per un carico eccessivo, le due sfere si abbassavano e facevano aumentare il flusso del vapore aprendo una valvola a farfalla così da far aumentare il numero di giri del motore; viceversa quando il numero di giri aumentava troppo il flusso di vapore veniva ridotto.
Vedere un esempio di applicazione all’indirizzo:
https://commons.wikimedia.org/wiki/File:Steam_engine_in_action_(two-thirds_speed).gif
E qui in Immagini d’epoca, l’articolo:
La centrale termoelettrica nelle Officine dell’Istituto Montani ricostruita su una documentazione parziale da integrare. Di Fabio Panfili,
 Se trascuriamo per ora l`azione della molla, il regolatore si basa sul concorrere di due forze: la cosiddetta forza centrifuga e la forza peso che agiscono sia sulle sfere visibili nelle foto, sia sui braccetti che sostengono le sfere.
 Due modelli più semplici per la sua comprensione sono il pendolo conico e un tipo di giostra molto diffuso nel quale i ragazzi seduti su un seggiolino sono appesi mediante robuste catene alla giostra.
 La forza centrifuga (diretta verso l`esterno) cresce con il prodotto del quadrato della velocità angolare moltiplicato per il raggio, mentre la forza peso (rivolta verso il basso) resta costante; pertanto le sfere tendono a sollevarsi allontanandosi dall`asse di rotazione (come si vede nel disegno) con un angolo di inclinazione la cui tangente è il rapporto tra la forza centrifuga e il peso.
 In questo modellino in realtà entra in gioco anche la forza della molla che tende a contrastare il sollevamento delle sfere fino a bloccarlo quando la molla è tutta contratta. La molla agisce mediante i braccetti trasversi forniti di uno snodo con una forza verso il basso F = – K x (legge di Hooke) e quindi il suo effetto cresce con l`innalzarsi delle due sfere.
 Le forze centrifughe si dicono apparenti, nel senso che appaiono solo in sistemi in rotazione.
Per intenderci meglio, facciamo un giro in giostra.
Mentre giriamo, sentiamo una forza che ci spinge verso l`esterno, diretta lungo il raggio; possiamo osservare che essa è più intensa in periferia che non vicino al centro e che agisce su tutti i corpi presenti sulla giostra, anche sugli oggetti che teniamo in tasca.
Un osservatore esterno però ci fornisce una versione molto diversa. Egli afferma che la nostra è solo una sensazione e che la vera forza che ci fa ruotare è diretta verso il centro ed è dovuta ai sostegni cui siamo appoggiati.
 Se infatti noi lasciamo i sostegni, non veniamo proiettati verso l`esterno, ma piuttosto in avanti nel senso del moto, e contemporaneamente la forza che sentivamo scompare come per magia. 
 La giostra è un sistema di riferimento non inerziale, mentre il sistema in cui si trova l`osservatore si può, con una certa approssimazione, definire inerziale.
Del resto le forze centrifughe non rientrano nella classificazione delle forze: gravitazionali, elettromagnetiche forti e deboli, inter-quark.La prima figura è a pag. 102 A Catalogue of Physical Instruments catalogue 17 L. E. Knott Apparatus Company Boston 1912, rinvenibile all’indirizzo:
https://archive.org/details/catalogofphyinst00knotrich?q=Catalogue+of+Physical+Instruments , e mostra come il modello era già usato nelle scuole dell’epoca.Così come la figura 855 di pag 84 del Catalog M Physical & Chemical Apparatus May 1912, Central Scientific Company. Chicago. U.S.A . Rinvenibile all’indirizzo:
https://www.sil.si.edu/DigitalCollections/trade-literature/scientific-instruments/pdf/sil14-51680.pdf
 Foto di Claudio Profumieri, elaborazioni, ricerche e testo di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.

 

 

Macchina di Palmieri, Santi Linari e Delezenne delle Officine Galileo Firenze.
Nell`inventario del 1956, in data 30-12-1968, al n° 4463 si legge: “Corrente campo terrestre”, probabile laconica descrizione di questa macchina del costo di ₤ 45.000.
Costruita dalle Officine Galileo di Firenze, anche se non ne riporta la sigla, essa è un generatore di corrente in C.C. e C.A. che, al posto del magnete permanente, sfrutta il campo magnetico terrestre, evidenziandone gli effetti.
Consiste in un telaio circolare di legno sul quale sono avvolte molte decine di spire di rame.
I capi dell’avvolgimento sono collegati ad un collettore costituito agli estremi da due anelli per ottenere un alternatore, mentre al suo centro vi è un anello spezzato per funzionare come dinamo. La macchina viene posta su un meccanismo che la fa ruotare e dunque, a seconda di come si collegano le spazzole, può generare o corrente continua o alternata, come si vede nella figura tratta dalle “Istruzioni per l’uso del nuovo apparecchio di rotazione” a cura di R. Magini. Dette istruzioni delle Officine Galileo – Firenze si trovano in una raccolta senza data risalente probabilmente agli anni ’40 -’50 del Novecento.
La figura B 315 si trova a pag. 37 del catalogo: Apparecchi per l’Insegnamento della Fisica a cura del prof. R. Magini, Officine Galileo, 1940.

Inizialmente questo apparecchio era un generatore di corrente a induzione elettromagnetica chiamato macchina telluro-magnetica (o semplicemente anello), dispositivo ideato indipendentemente da Luigi Palmieri (1807-1896) nel 1845 (che però pare certo abbia condiviso il progetto col Prof. D. Santi Linari) e da C. E. Delezenne ( 1776-1866) fisico francese. Vedere in proposito della vicenda dei due italiani: Raccolta Fisico-Chimica Ossia Collezione di Memorie di F. Zantedeschi, 1847.
Una figura del tutto simile a questa (tranne per le scritte in inglese) si trova a pag. 1011 di
Elementary Treatise on Physics Experimental and Applied translated from Ganot’s Éléments De Physique by E. Atkinsons, W. Wood & Co. New York 1910. Rinvenibile all’indirizzo:
https://archive.org/details/treatphysics00ganoric .
Abbiamo qui voluto riportare diversi disegni tratti da cataloghi e libri dei primi del Novecento che attribuiscono la macchina sia a Palmieri sia a Delezenne.Le figure 8231 e 8232, con opportune modifiche, sono a pag. 735 del Catalogue des Appareils pour l’Enseignement de la Physique construit par E. Leybold’s Nachfolger Cologne, 1905; rinvenibile all’indirizzo:
http://cnum.cnam.fr/PDF/cnum_M9915_1.pdf .
La figura 1246 è a pag. 184 di Illustrated and Descriptive Catalogue of Physical Apparatus F. E. Becker & Co., 1924; rinvenibile all’indirizzo:
http://cnum.cnam.fr/PDF/cnum_M9847.pdf

La figura 8706 è a pag. 292 del Physikalische Apparate Ferdinand Ernecke Berlin S.W. Preiliste N° 18. Rinvenibile all’indirizzo:
https://www.sil.si.edu/DigitalCollections/trade-literature/scientific-instruments/files/51667/

La stessa figura (Fig. 524) si trova a pag. 552 dell’edizione italiana del Ganot: Trattato di Fisica di A. Ganot, versione del Dott. G. Gorini, F. Pagnoni, Milano 1861. Rinvenibile all’indirizzo:
https://ia802506.us.archive.org/9/items/bub_gb_1BsQibxllmYC/bub_gb_1BsQibxllmYC.pdf
La figura 81-155 è a pag. 380 di A Catalogue of Physical Instruments, catalogue 17 L. E. Knott Apparatus Company Boston 1912; rinvenibile all’indirizzo:
https://archive.org/details/catalogofphyinst00knotrich?q=Catalogue+of+Physical+Instruments .
E per ultima:

Foto di Federico Balilli, elaborazioni, ricerche e testo di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.