Categoria: fisica

   Pendolo compensato di Harrison
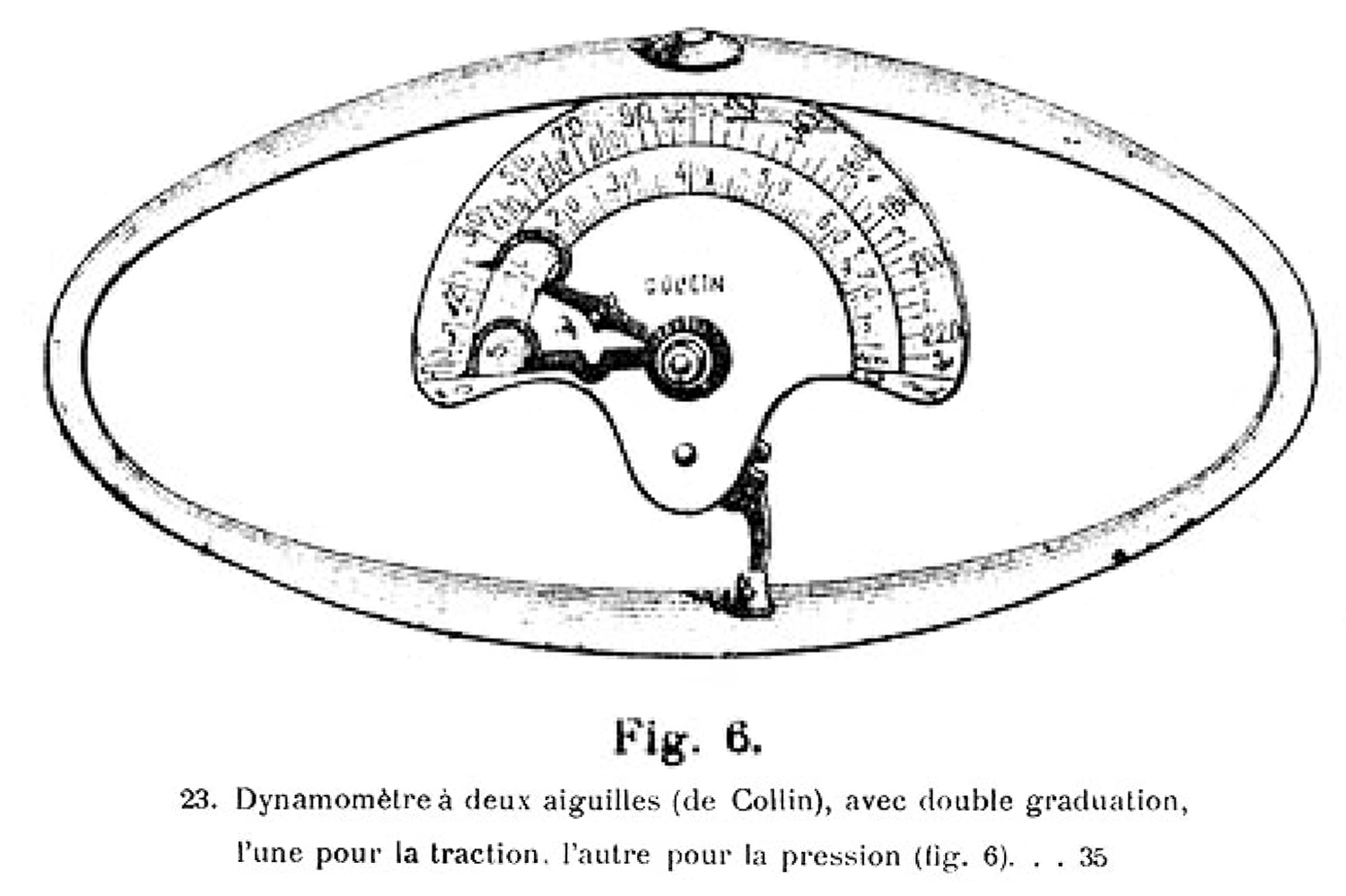
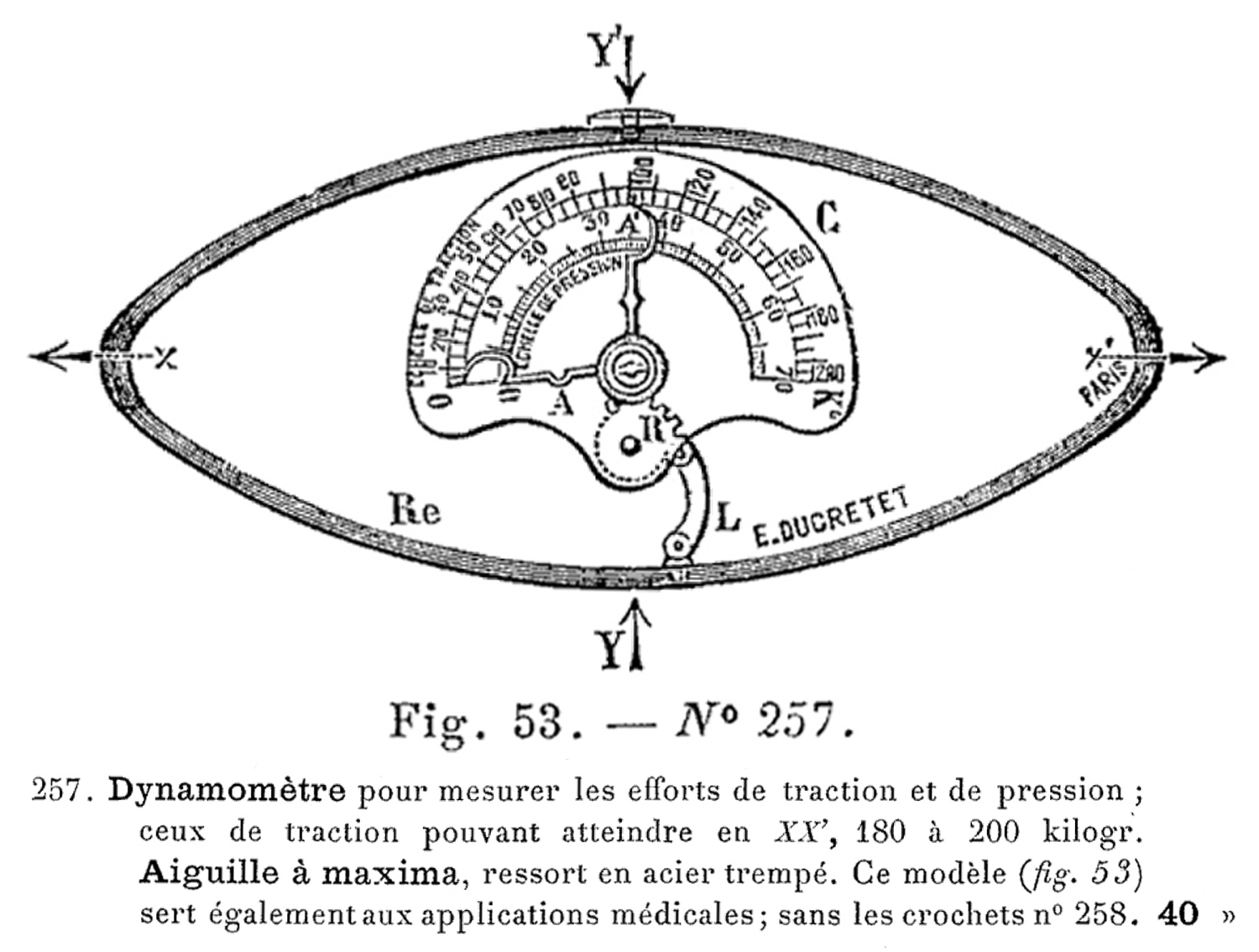
Nell`inventario del 1906 a pag. 232 n° 822 viene detto già esistente e descritto come: “Pendolo compensatore a 9 azze”.
Nell’inventario del luglio del 1912, pag. 50 n° 855 viene descritto come: “Pendolo compensatore a 9 branche di acciaio e ottone con supporto”.
Il periodo di un pendolo fisico, cioè il tempo che impiega a compiere una oscillazione completa, dipende dal suo momento di inerzia e dalla distanza tra il suo baricentro e il punto di sospensione.
Una variazione di temperatura dell`ambiente in cui il pendolo è collocato, provoca una variazione delle sue dimensioni e di conseguenza del suo periodo.
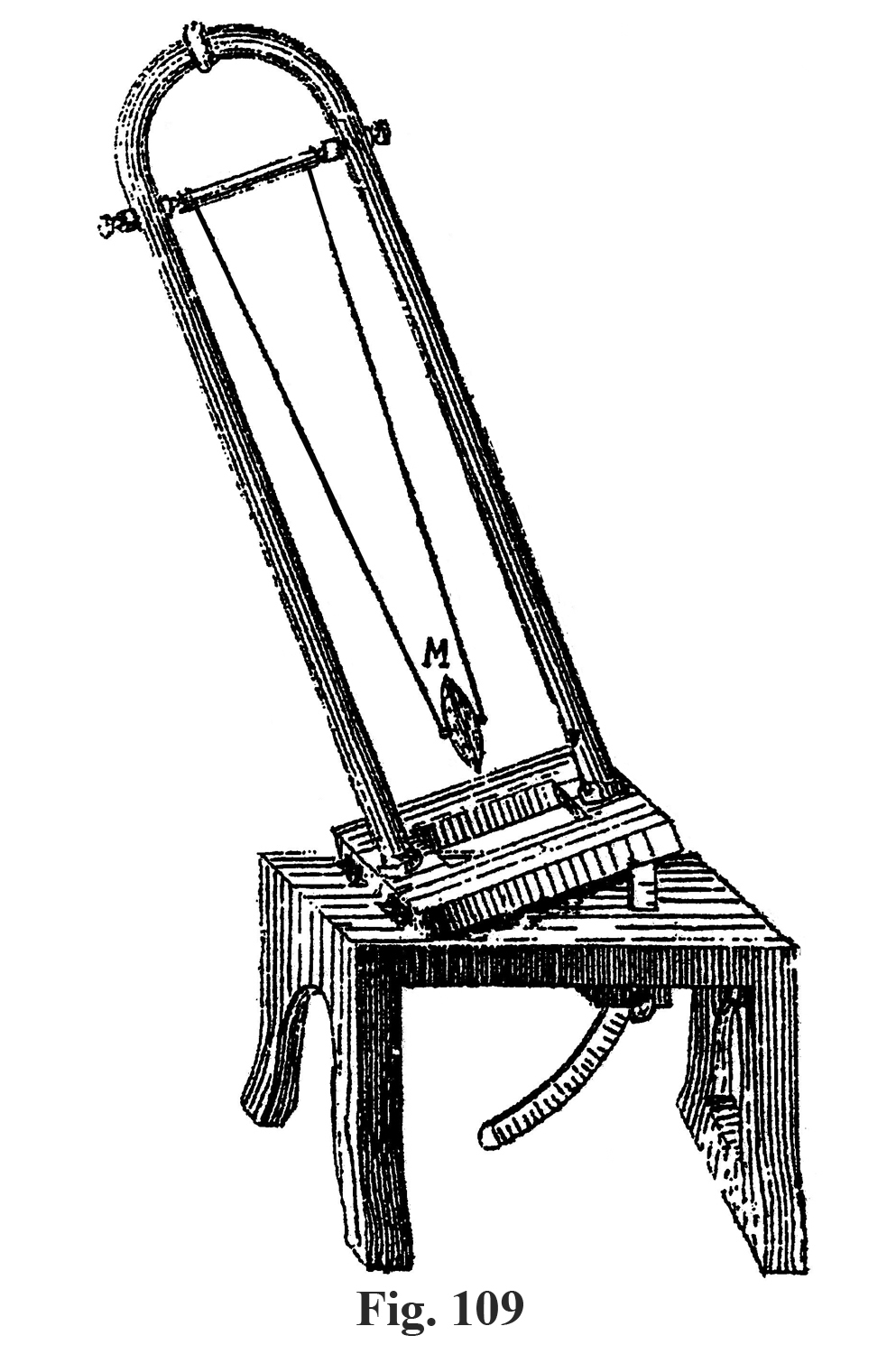
Galileo aveva osservato che, per piccole oscillazioni di un pendolo semplice, il periodo non dipende dalla loro ampiezza, e nel 1641 ideò un regolatore a pendolo per orologi di cui ci è pervenuto il disegno di V. Viviani.
Però, l`applicazione del pendolo all`orologio che ebbe amplissima diffusione, fu ideata da C. Huygens forse nel 1657; egli pubblicò sia la teoria completa del pendolo che i dettagli della costruzione di orologi col sistema “scappamento ad ancora” nel 1673 nel suo “Horologium Oscillatorium”.

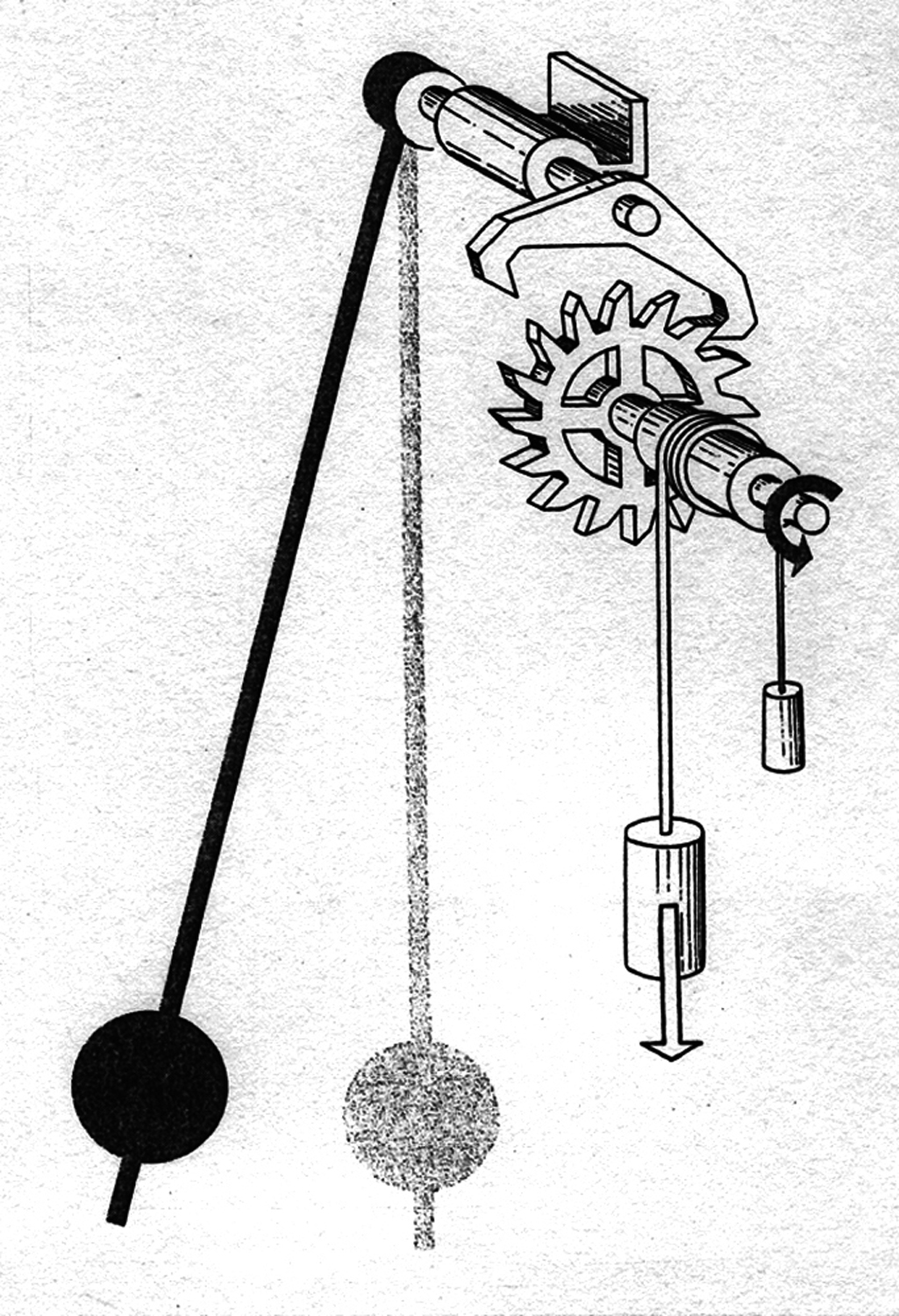
In un comune orologio a pendolo si può mutare la lunghezza dello stesso agendo su una vite; la deriva si corregge per tentativi confrontando giornalmente l`ora segnata con un tempo campione (segnale radio, ad esempio).
Nella costruzione di un buon pendolo per un orologio meccanico di precisione si usano particolari accorgimenti per renderlo insensibile alle variazioni di temperatura.
Un sistema molto diffuso è il pendolo a compensazione.
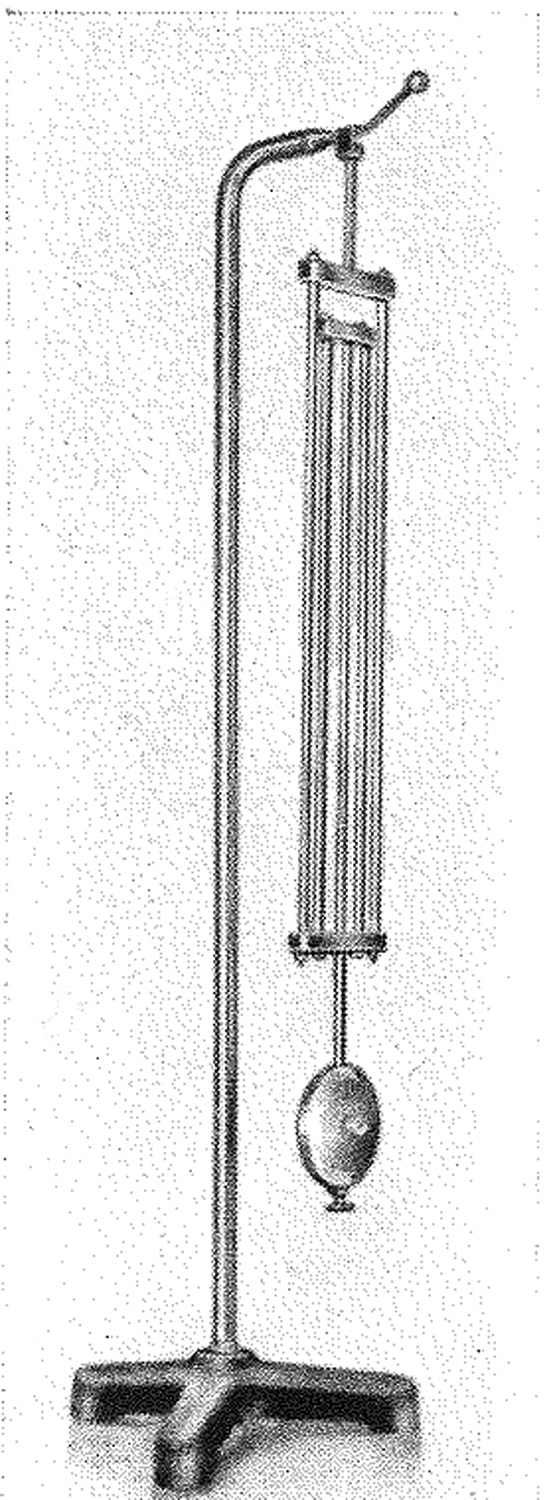
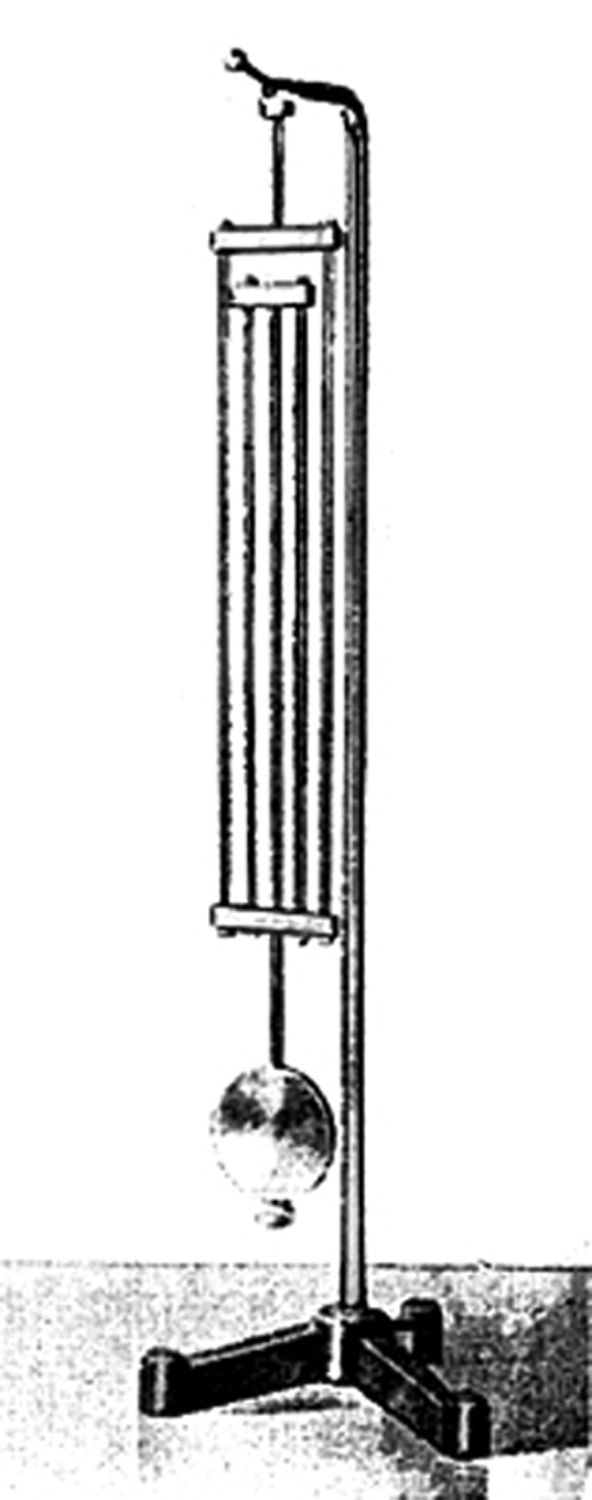
L`esemplare del Montani è del tipo Harrison.
Il sistema di più aste che sorregge la massa lenticolare oscillante è fatto con sbarrette di due materiali a diverso coefficiente di dilatazione: le sbarrette che si dilatano verso il basso sono di acciaio, mentre quelle che si dilatano verso l’alto sono di ottone; la loro lunghezza è stata scelta in modo tale che le dilatazioni, dovute alle variazioni di temperatura ambiente, si annullino a vicenda. In tal modo il periodo di oscillazione resta invariato.
J. Harrison nel 1762 vinse una parte di un premio di 20.000 sterline per avere costruito il migliore cronometro nautico, la cui precisione è essenziale nella navigazione per determinare la longitudine.
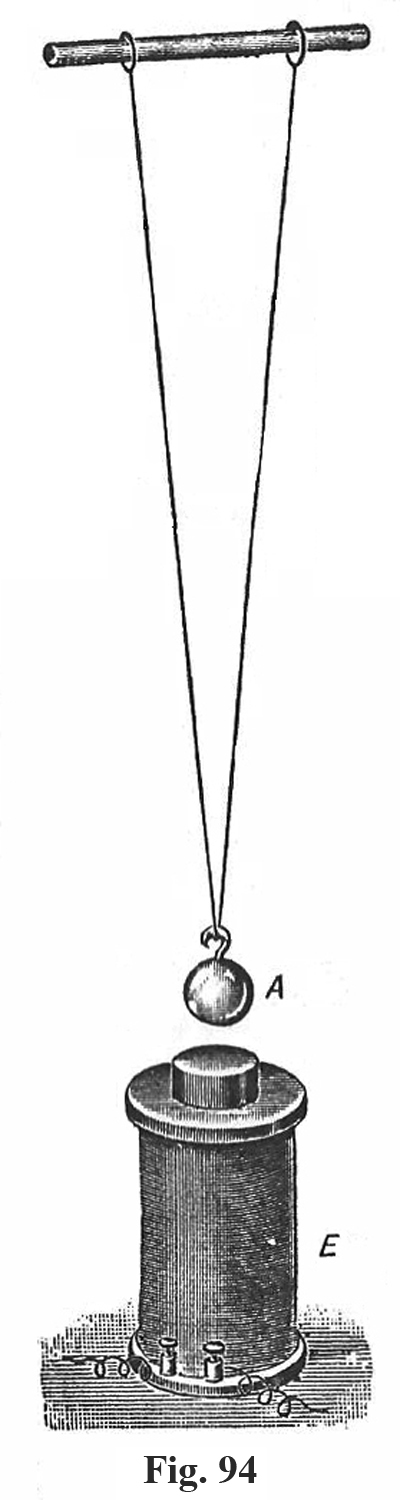
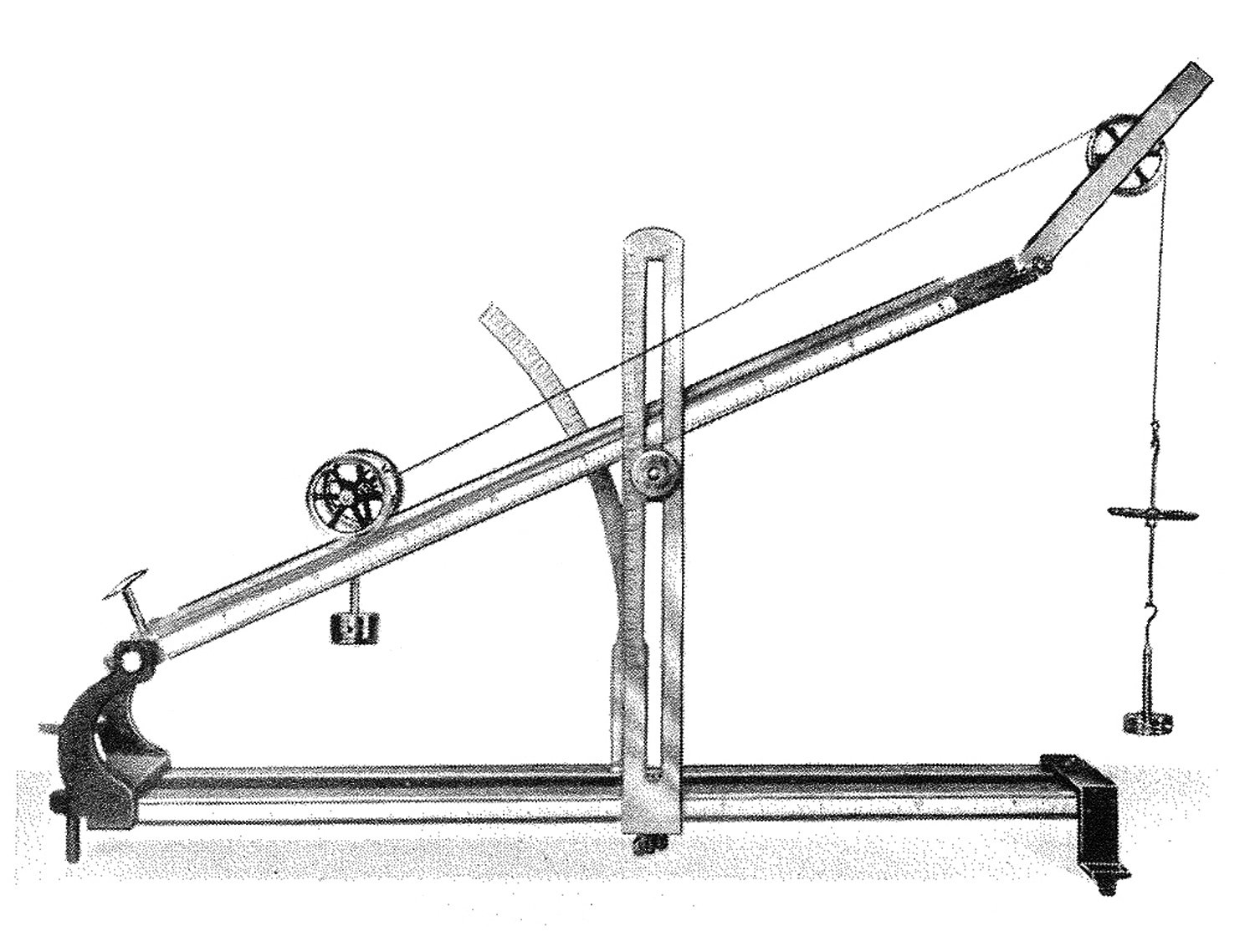
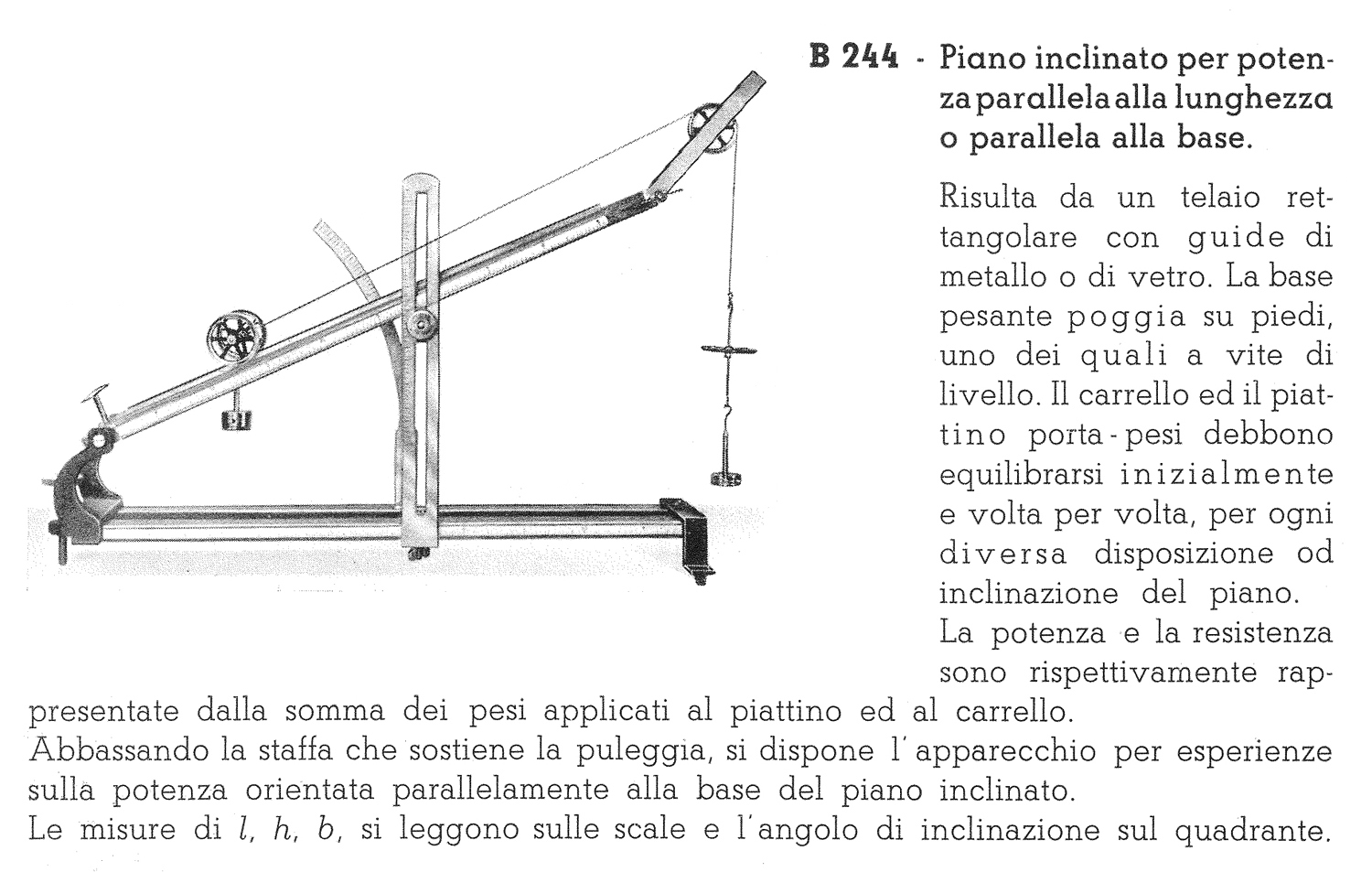
La figura B333 è a pag. 44 del catalogo Apparecchi per l’Insegnamento della Fisica a cura del prof. R. Magini, Officine Galileo, 1940.
Anche l’ultima figura è tratta da un catalogo delle Officine Galileo di Firenze.
Bibliografia.
M. Guidone, La misura del tempo e il battito del polso, Il Montani n° 1-2, Fermo. Giugno 2002.
A. Battelli e P. Cardani, Trattato di Fisica sperimentale, Vol. I, F. Vallardi, Milano 1913.
G. Goretti Miniati, Elementi di Fisica, Vol. II, F. Cuggiani, Roma 1909.
B. Dessau, Manuale di Fisica, Vol. II, SEL, Milano 1938.
AA. VV., PPC Progetto Fisica, Zanichelli, Bologna 1986.
S. Donati, Nozioni di fisica, Lattes & C., Torino 1972, da cui è stata tratta la figura del sistema scappamento ad ancora.
Foto di Daniele Maiani, elaborazioni, ricerche e testo di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.

 

 

 

 

      Pendolo di Mach.
Inventario D del 1937, n° 212.
È un pendolo fisico particolare ideato per ricavare la relazione tra il periodo T e l’accelerazione di gravità g.
Infatti, senza variare la sua lunghezza cioè senza variare la posizione della massa mobile, fornisce la possibilità di variare in modo noto l’accelerazione a cui è soggetto, cambiando l’angolo di inclinazione α del piano di oscillazione rispetto alla verticale secondo l’espressione
  a = g cos α.
Ciò è didatticamente molto interessante in quanto non è affatto agevole mostrare, con un pendolo semplice, la dipendenza del periodo T dalla accelerazione di gravità g.
Per fare una simile dimostrazione a volte  si ricorre ad un elettromagnete posto sotto la massa di acciaio di un pendolo semplice: non appena si eccita l’elettromagnete, si nota che il pendolo oscilla più rapidamente poiché l’attrazione magnetica simula un aumento della forza di gravità. Si può variare l’attrazione magnetica regolando opportunamente la corrente nell’elettromagnete.
Ma questo artificio non ha l’eleganza del pendolo di E. Mach (1838-1916).

La figura 94 relativa a quest’ultima soluzione è stata tratta da pag. 82 di L. Segalin, Fisica sperimentale, Vol. I, G. B. Paravia & C., Torino 1933.

La figura B 323 è a pag. 40 del catalogo: Apparecchi per l’Insegnamento della Fisica a cura del prof. R. Magini, Officine Galileo, 1940. L’ultima figura è stata tratta da un catalogo delle Officine Galileo.
Bibliografia.
A. Cantoni, L’esperimento fisico, U. Hoepli, Milano 1938, da cui è stata tratta la figura 62 di pag. 109 dove è scritto: «Per eseguire l’esperienza le Officine Galileo mettono in vendita l’apparecchio di Mach (vedi fig. 62) …».
A. Battelli e P. Cardani, Trattato di fisica sperimentale, Vol. I, F. Vallardi, Milano 1925, da cui è stata tratta la figura 109 di pag. 116.
Il pendolo è esposto al Museo MITI, su proposta di Fabio Panfili.
Foto di Daniele Maiani, elaborazioni, ricerche e testo di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.

 

 

 

 

 

 

 

Pendolo reversibile di Kater della ditta Leybold.
Detto anche pendolo geodetico poiché serve per misurare l`accelerazione di gravità locale.
Matricola N° 346 11, made in Germany.
Nell`inventario D del 1956, in data 6 maggio 1964, al n° 3737 si legge: “Pendolo reversibile su treppiede”.
Questo pendolo fisico è reversibile nel senso che può oscillare rispetto a due “punti” diversi costituiti dai due coltelli di sospensione posti lungo l`asta con il fulcro a V, situato in alto sul sostegno.
La lunghezza dell`asta è di 1,625 m; la distanza tra i coltelli è di 0,95 m; le due masse scorrono lungo l`asta e possono essere fermate per mezzo di una vite in qualunque posizione: una massa reca la scritta 1000 g e il N° 346 11, mentre l`altra è di 1400 g.
Sull’asta i due coltelli di acciaio temperato sono in posizione simmetrica rispetto al centro. Per mezzo di essi il pendolo può essere sospeso su di un piano di acciaio duro  (con il fulcro a V) sistemato all’estremità superiore di un pesante stativo con piedi regolabili. Lo strumento è realizzato in maniera tale che i centri di massa delle varie parti costituenti siano allineati su di una retta, intersecante gli assi definiti dai coltelli. In tale modo l’oscillazione del pendolo può essere confinata (nei limiti sperimentali) ad un piano verticale, ortogonale all’asse orizzontale di rotazione e passante per il centro di massa del sistema.
Il procedimento è il seguente: si misura il periodo T del pendolo appeso ad un coltello e con le masse in una certa posizione; poi si rovescia il pendolo e si ripete la misura di T; quindi  si confrontano i valori dei due periodi; poi si spostano le masse per tentativi successivi fino ad ottenere l`uguaglianza dei due periodi (nei limiti degli errori sperimentali).
Si tenga presente che il pendolo si muove di moto armonico solo per oscillazioni di piccola ampiezza (dell`ordine di 10°) per le quali dunque vale la legge del periodo che sarà usata.
Al solito, per avere una buona misura di T si consiglia di misurare il tempo di almeno 20 oscillazioni complete e di dividere il tempo ottenuto per 20; in tal modo si diminuisce l`errore dovuto ai riflessi di chi cronometra.
Per determinare il valore dell`accelerazione di gravità g, una volta raggiunta l`eguaglianza tra i due periodi rispetto ai due coltelli di sospensione, si usa la formula
g = 4 π ² l / T ².
Dove l è la distanza tra i due coltelli.
La teoria che mostra la validità di questo motodo è piuttosto complessa e non è questa la sede per illustrarla; si tenga conto comunque che altre fonti di errore sono: la temperatura che influenza la lunghezza fra i coltelli, l`attrito tra questi e la sospensione, e l`effetto dell`aria che rallenta il moto.
Il pendolo reversibile fu ideato dall` ingegnere francese Gaspard Claire François Marie Riche barone di Prony (1755 – 1839), ma le esperienze furono realizzate dal geodeta inglese Henry Kater (1777 – 1835) che mostrò come il valore dell`accelerazione di gravità diminuisce dai poli all`equatore.
Per chi desidera approfondire gli argomenti trattati, si consiglia di leggere una esauriente spiegazione al seguente indirizzo:
https://www.fisica.uniud.it/~santi/didattica/kater.htm
Foto di Claudio Profumieri. elaborazioni, ricerche e testo di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.

 

 

 

 

Piano inclinato Officine Galileo  Firenze.
Nell’inventario generale n° 6 del 1925 a pag 68, n° 2227/126, si legge: “Officine Galileo Firenze. Piano inclinato nuovo modello. ₤ 376”.
Nell’inventario del 1926 al n° 645-2227 si legge di nuovo: “Officine Galileo Firenze. Piano inclinato nuovo modello. ₤ 376”.
Il piano inclinato riveste un ruolo importante nella storia della fisica, visto dapprima come macchina semplice utile per sollevare oggetti pesanti fin dalla più remota antichità, poi da Galileo Galilei come mezzo di indagine sulla caduta dei gravi e, in questo contesto, il suo studio assume un aspetto fondamentale nella storia della fisica.
Galileo infatti, non potendo studiare come cadevano i corpi per l’impossibilità di misurane i tempi di caduta, fece l’ipotesi alquanto azzardata che il moto lungo un piano inclinato segue le stesse leggi del moto di caduta, se si possono trascurare gli attriti.
Il piano inclinato gli permetteva infatti di ottenere piccole accelerazioni con tempi di discesa misurabili col suo orologio ad acqua.
Ma, essendo Galileo il primo ad eseguire un simile esperimento, ignorava altri aspetti cruciali che comportavano errori all’epoca inevitabili. (Vedi sia il disegno di G. Gamow sia il dipinto di G. Bezzuoli del 1841, riportati qui sotto).

 Questo esemplare serve principalmente nell’insegnamento della statica ed è costituito da un telaio rettangolare con guide, che può ruotare intorno ad un asse posto all’estremità in basso, permettendo di scegliere l’inclinazione del piano e quindi l’altezza h. All’altra estremità c’è una staffa snodata, provvista di una puleggia, che, opportunamente orientata, permette di ottenere la direzione della forza equilibrante o parallela al piano “l” o parallela alla base “b”.
Al carrellino può essere appesa una massa aggiuntiva.
Nel caso della direzione della forza F parallela al piano “l” si può mostrare come varia la componente parallela al piano inclinato del peso dell’oggetto, posto sul piano stesso, al variare dell`angolo α formato da “l” rispetto all’orizzontale. Per fare ciò si procede nel modo seguente: inclinato il piano di un certo angolo α, si sceglie il peso da aggiungere al carrellino a due ruote, a sinistra nella foto, poi si cerca di equilibrare il tutto con alcuni pesetti posti a destra sotto la puleggia. Siccome i pesetti usati normalmente in laboratorio sono tra loro uguali, si ottiene l’equilibrio variando leggermente l’angolo di inclinazione e si prende nota delle grandezze l, h, α. Lasciando invariato il peso complessivo del carrellino, si sceglie un angolo maggiore tentando di nuovo di ottenere l’equilibrio dapprima aumentando il numero dei pesetti sotto la puleggia, poi aggiustando l’angolo, fino a mostrare che vale:
F = P sen α
dove P è il peso sul piattello di destra e F è la componente parallela al piano di cui sopra. Ovvero:
F / P = h / l
dove h è l’altezza e l è la lunghezza del piano.Nel caso della forza F parallela alla base b si può mostrare che vale:
F = P tang α ovvero: F / P = h / b
con una procedura simile a quella precedentemente descritta.

Questo apparecchio non permette misure quantitative per esperimenti di dinamica o sulla conservazione dell’energia meccanica, poiché non è agevole misurare il tempo di discesa del carrellino durante il moto.
Esso può comunque essere utile per una dimostrazione qualitativa, introduttiva di quegli argomenti, facendo osservare agli allievi il comportamento dei corpi in moto, sia al variare dei pesi sia al variare dell’angolo di inclinazione.
La figura con Galileo è stata tratta da G. Gamow, Biografia della Fisica, EST Mondadori, Milano 1963.
La figura B 244 si trova a pag. 12 del catalogo: Apparecchi per l’Insegnamento della Fisica a cura del prof. R. Magini, Officine Galileo, 1940.

Il piano inclinato è esposto al Museo MITI, su proposta di Fabio Panfili.
Foto di Daniele Maiani, elaborazioni, ricerche e testo di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.

 

 

 

 

 

 

Piccolo dinamometro tipo Collin.
Privo di marca, non rinvenibile negli inventari e di difficile datazione, forse risalente ai primi del Novecento.
È un dinamometro in miniatura che ricorda il tipo Regnier.
Ho trovato diversi cataloghi Collin, tutti con la figura del piccolo dinamometro simile a questo esemplare. Ad esempio all’indirizzo:
http://cnum.cnam.fr/PDF/cnum_M9865.pdf
si trova il Collin Fabrique d’Instruments de Chirurgie. Instruments pour l’Antropologie et l’Antropométrie, del 1930; e a pag. 3 vi è la fig. 6 riportata qui sotto, con la scritta: «23. Dynamomètre à deux aiguilles (de Collin), avec double graduation, l’une pour la traction, l’autre pour la pression (fig. 6)».
Inoltre ho trovato un disegno di un dinamometro sempre simile a questo in un catalogo del 1905 di E. Ducretet, costruttore di Parigi. All’indirizzo:
http://cnum.cnam.fr/PDF/cnum_M5591.pdf
si trova il Catalogue Raisonné des Instruments de Précision de E. Ducretet.
A pag. 45 vi è la figura qui sotto riportata con la seguente didascalia: «Dynamomètre pour mesurer les efforts de traction et de pression; ceux de traction pouvant atteindre en XX’, 180 à 200 kilogr. Aiguille à maxima, ressort en acier trempé. Ce modèle (fig. 53) sert également aux applications médicales; sans les crochets n° 258. 40 Francs», cioè: «Dinamometro per misurare gli sforzi (muscolari) di trazione e di pressione, quelli di trazione possono raggiungere in XX ‘, 180 e 200 kg. Ago di massima, balestra in acciaio temperato. Questo modello è utilizzato anche per applicazioni mediche, senza i ganci n° 258».
Lo strumento misura sia la compressione, esercitata da una mano serrata sullo strumentino in Y Y’ nella figura; sia la trazione fatta con entrambe le mani in X X’.
Non si è indagato sulla veridicità delle unità di misura riportate nelle due scale: quella di trazione corrisponde alle caratteristiche del Ducretet: 200 -K- 0 fondo scala, mentre la scala di compressione arriva a 70, come si vede bene nelle foto.
Prima della misura si azzera il tutto, l’indice a sinistra è collegato alla piccola balestra di forma ellittica mediante una levetta e un ingranaggio, mentre quello più a destra è folle.
Durante la prova l’indice a sinistra sposta l’altro fino al massimo valore raggiunto e, a prova terminata, ne permette la comoda lettura. Se in una prova successiva il valore della compressione risultasse maggiore, lo strumentino ne permetterebbe il confronto.
Durante alcune prove, svolte per diletto, il Sig. Gaetano Marini (della Segreteria Didattica) ha agevolmente superato il fondo scala in entrambi i modi d’uso dello strumento, mentre altri sono arrivati solo a metà nella prova di compressione e hanno trovato grosse difficoltà nella prova di trazione.
Dopo la pubblicazione della prima versione di questa scheda, il 20 febbraio del 2014 il Prof. Emerito Jean-Francois Loude di Losanna mi scriveva: «Dear Dr. Panfili, concerning the “Piccolo dinamometro tipo Ducretet”. As I am currently preparing a presentation about “Early Dynmometers”, what I can say is the following.
The Regnier Dynamometer, described in 1798, was still manufactured, without significant changes, late in the XIXth c. – you have one by Santarelli. For medical and para-medical uses, it was too large. According to Broca (Instructions générales …, 1862 and 1875), a smaller dynamometer, with the dial inside the oval, closed spring was designed by Mathieu in the early part of the second half of the XIXth c. It was manufactured by the “Maison Collin”, and thus is known as the “Collin dynamometer”, still produced, sold and used today. Google it and you will find many sellers! I don’t know who was the actual maker of your small Collin dynamometer. Ducretet was probably the seller of a common apparatus. …».
Traduzione: «Caro Dottor Panfili, riguardo al  “Piccolo dinamometro tipo Ducretet”. Dato che sto preparando una presentazione su “antichi dinamometri”, posso darle le seguenti informazioni. Il dinamometro Regnier è stato fabbricato senza significativi cambiamenti come il modello del 1798 fino al tardo XIX secolo. Voi ne avete uno prodotto da Santarelli. Esso però era troppo grande per usi medici e paramedici. Stando a Broca (Instructions générales, 1862; 1875) all’inizio della seconda metà del XIX secolo Mathieu progettò un dinamometro più piccolo, con la scala graduata all’interno della molla chiusa e ovale. Veniva prodotto dalla “Maison Collin”, da qui il nome “Dinamometro Collin”, il quale viene tutt’oggi ancora prodotto, venduto e usato. Cercalo su Google e troverai molti rivenditori! Non so chi sia il produttore del tuo piccolo dinamometro Collin. Ducretet era probabilmente il venditore [o rivenditore N.d.T] di attrezzature generiche».
Ringrazio il Prof. Loude sia per le preziose informazioni, sia per avermi inviato il catalogo Collin [Maison Charrière, Collin, Fabrique d’Instruments de Chirurgie, Paris (collezione P. Brenni)] ed un depliant del 1921 nel quale si vede il Prof. di Psicologia Elementare Éduard Claparède che usa il dinamometro Collin in trazione.
Foto di Claudio Profumieri, elaborazioni, ricerche e testo di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.