Categoria: fisica

Generatore-Motore in C.C. C.A. PHYWE a magnete permanente da dimostrazione.
  Nell`inventario del 1956, al n° 933 si legge: “Modello scomponibile di motorino elettrico – in esistenza”.
La definizione data non è appropriata, ma il numero di inventario riportato sull`etichetta posta su questo esemplare coincide.
Come si vede nelle foto, questo modello di piccole dimensioni per uso squisitamente didattico è costituito da un magnete permanente ad U sormontato dal dispositivo che può ospitare sia il tamburo per la corrente alternata C.A. con il collettore a tre anelli, sia il tamburo con il collettore ad anello spezzato per la corrente continua C.C. .
Esso dunque può funzionare da motore sia in C.C. sia in C.A. semplicemente cambiando il rotore, posizionando opportunamente le spazzole e alimentandolo con tensioni dell`ordine di 6/8 V.
Mentre per fare una dimostrazione come generatore sia in C.C. sia in C.A. si sceglie il rotore opportuno, si posizionano le due spazzole e si gira la manovella o lo si fa ruotare con una macchina apposita mediante una cinghia.
Per misurare la tensione generata, che si aggira sui 3 o 4 V, si usa un voltmetro di portata idonea; per misurare la corrente si usa un amperometro da pochi mA fondo scala; oppure si può mettere una lampadina di pochi volt (3,5 V /0,2 A) come carico per mostrare qualitativamente l`energia generata. Come si vede nelle foto, il tamburo per C.C. è un anello Pacinotti con il collettore diviso in 4 settori.
Il dispositivo è stato sottoposto a prove di funzionamento dall`ing. Claudio Profumieri ed ha dato buoni risultati.
Bibliografia: Schede di istruzioni Phywe Göttingen del 1958 E 3351; E 35123; E 35124.
Foto di Claudio Profumieri, elaborazioni, ricerche e testo di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.

 

 

 

 

Goniometro da dimostrazione tipo Noack.
Inventario D del 1937 n° 317.
Il goniometro tipo Noack serve essenzialmente per misurare l`angolo compreso tra due facce piane riflettenti (ad esempio di un prisma o di un cristallo) di un oggetto ottico. Serve inoltre per la misura degli angoli di deviazione di prismi ottici o di liquidi, messi in apposite vaschette, e quindi per la ricerca dei relativi indici di rifrazione.
Ma se al posto di questi oggetti si mette un prisma ad alta dispersione, il goniometro diventa uno spettroscopio del tipo Kirchoff e Bunsen.
Sopra una massiccia piattaforma circolare sono disposti radialmente il collimatore e il collettore, provvisti di obiettivi uguali.
La piattaforma reca sul lembo le incisioni in gradi.
Il collimatore ha una fenditura nel fuoco di una lente, è girevole sulla piattaforma e la lettura della sua posizione si fa osservando l`indice scorrevole sul lembo graduato della piattaforma.
Il collettore è formato da una lente che proietta l`immagine su uno schermo traslucido, anch`esso è girevole sulla piattaforma e la sua posizione si determina per mezzo di un indice così come col collimatore.
Su un piattino centrale, girevole e munito di indice, si dispone l`oggetto ottico di cui si vuole misurare l`angolo. Il piattino porta incisa una croce di riferimento.
L`aspetto dello strumento sembra di fattura piuttosto artigianale; inoltre la lettura per mezzo degli indici è rudimentale in quanto non apprezza che il grado sessagesimale. Tutto ciò fa pensare che il suo uso fosse limitato a una dimostrazione qualitativa.
Ne ignoriamo il costruttore.
Le figure IX-1 e IX-2 mostrano un goniometro Noack costruito dalle Off. Galileo che permette misure più accurate.
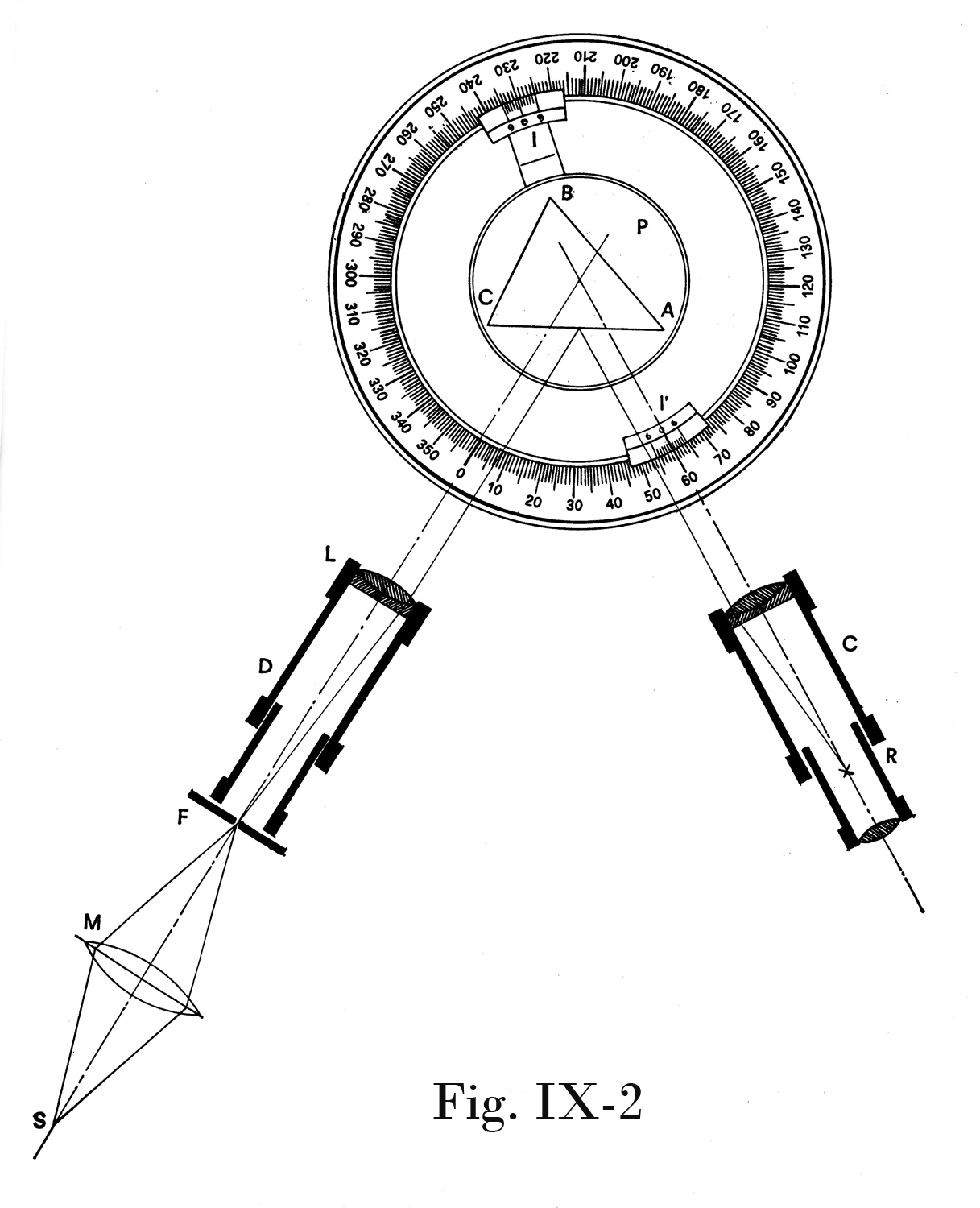L`uso del goniometro Noack, per la misura dell`angolo tra due facce, richiede una preparazione attenta che si divide in due fasi: prima si fa una messa a punto senza l`oggetto ottico in esame; poi si pone questo sul piattino e si procede per tentativi fino ad avere l`immagine della fenditura, riflessa dalla faccia dell`oggetto, bene a fuoco sullo schermo traslucido. Fatto ciò si rileva l`angolo ß , leggendo la posizione dell`indice del piattino sul lembo graduato della piattaforma. Poi si ruota il piattino fino a che l`immagine, riflessa dalla seconda faccia dell`oggetto sullo schermo opalino, sia nella stessa posizione della precedente e si misura il secondo angolo δ. Si trova infine che ß – δ = 180° – x , dove x è l`angolo tra le due facce dell`oggetto ottico in esame.
Ben più complessa è la procedura per la misura dell’indice di rifrazione.
La misura dell’angolo di rifrangenza di un prisma col metodo del cannocchiale fisso o del prisma girevole è rappresentato nelle figure IX-4 e IX-6. 

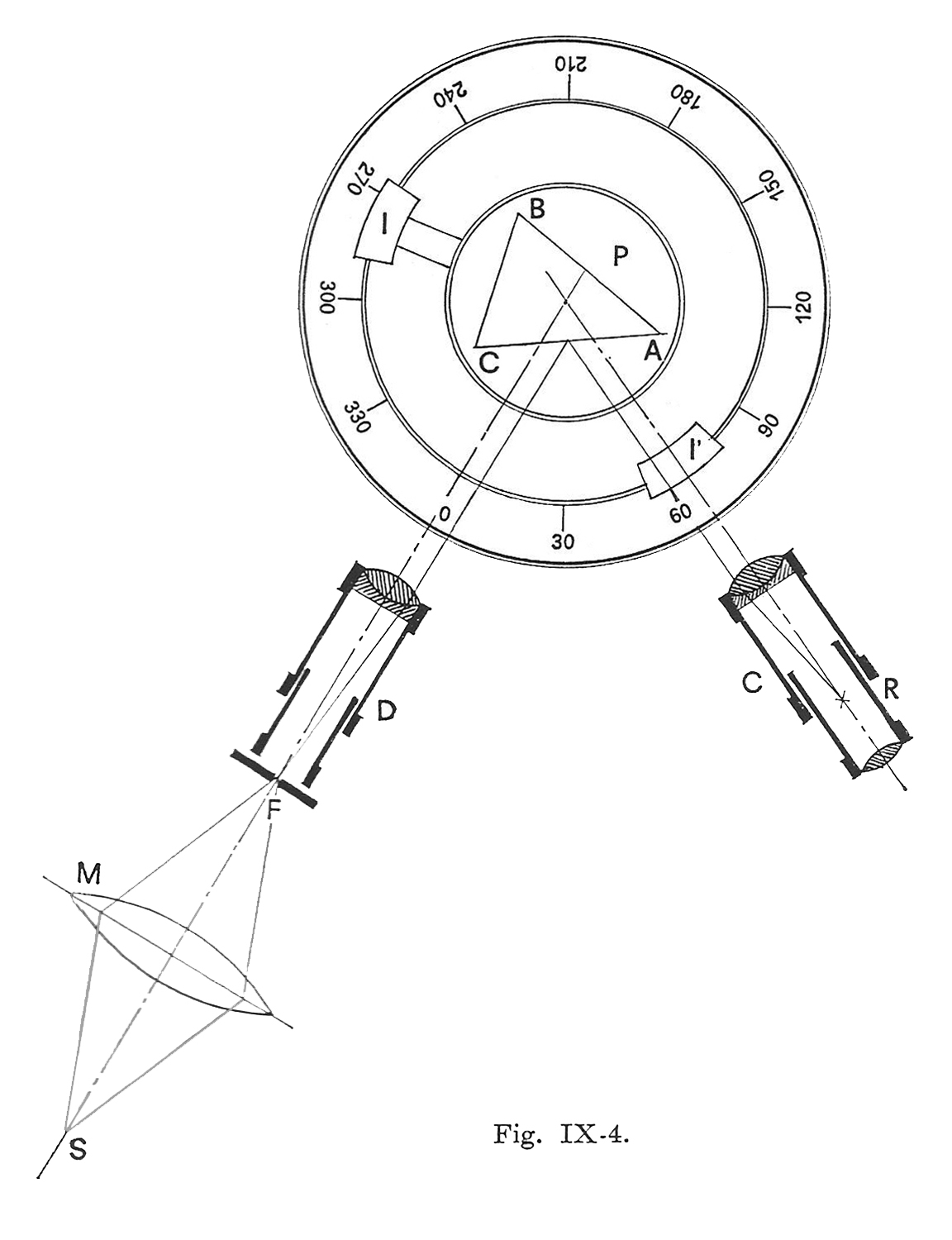
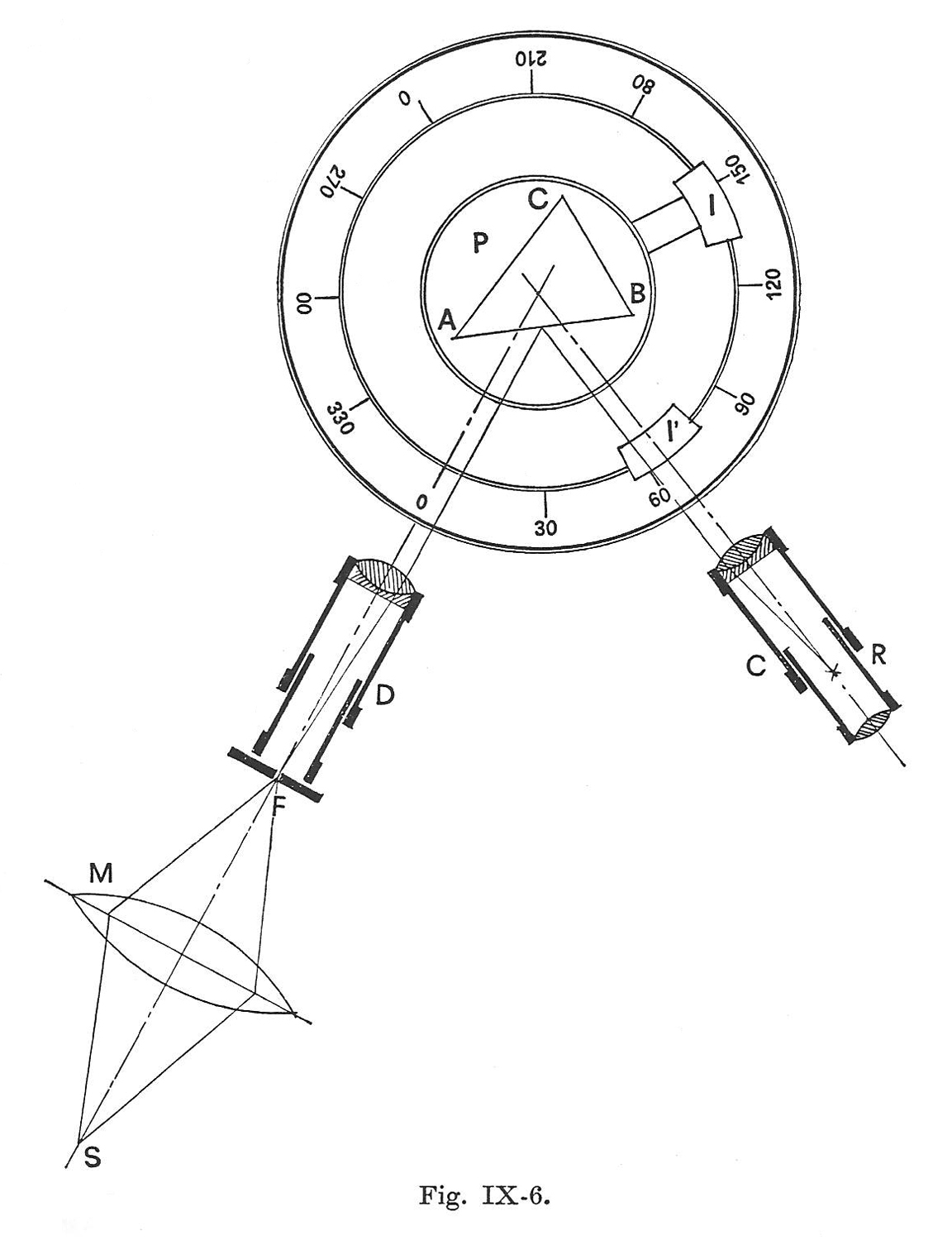
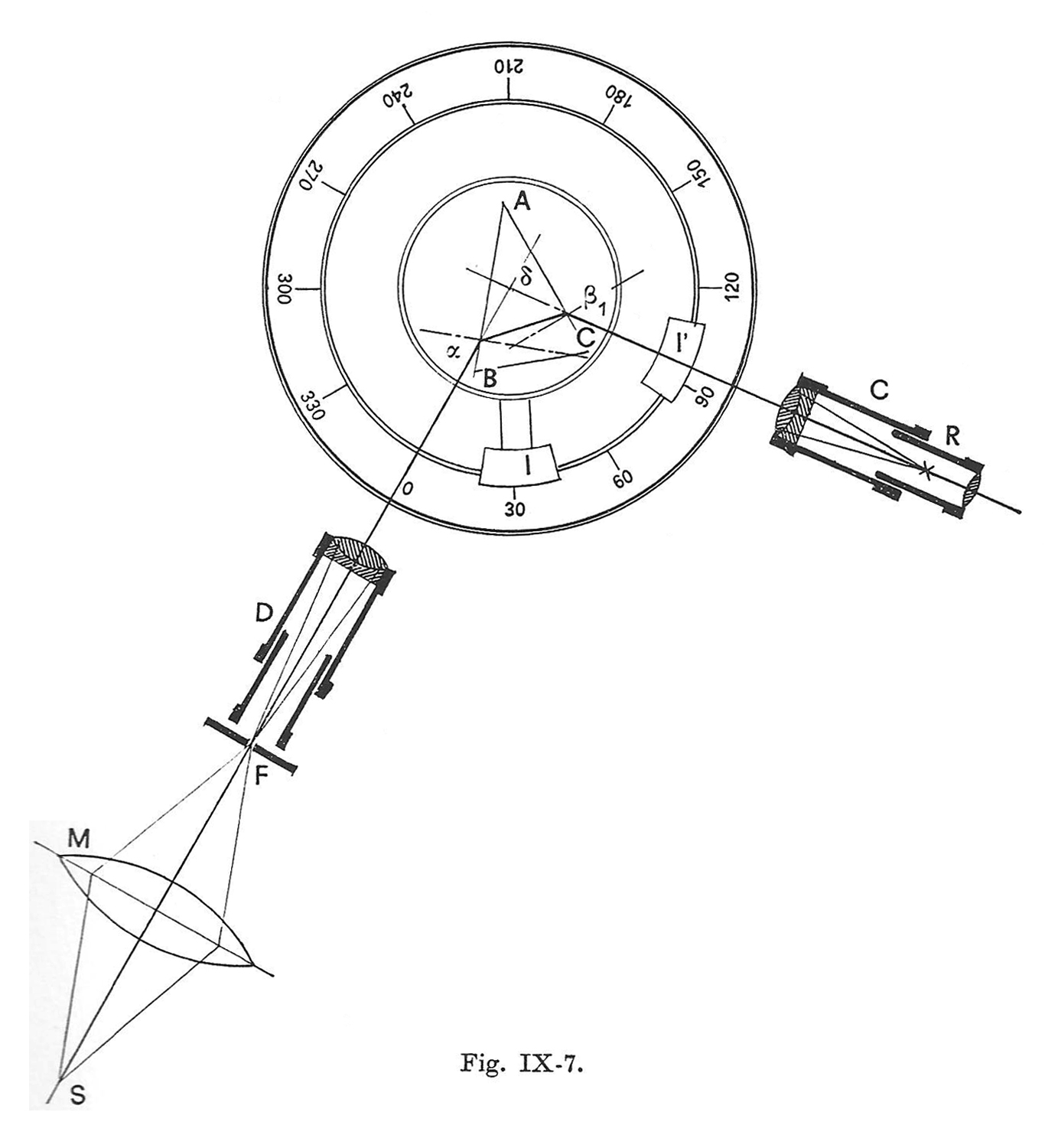
La misurazione dell’angolo di deviazione minima è
rappresentata nelle figure IX-7 e IX-8. Queste lunghe procedure sono descritte minuziosamente in Complementi di fisica e laboratorio (vedere Bibliografia).

La figura A 141 si trova a pag. 54 del catalogo: Apparecchi per l’Insegnamento della Fisica a cura del prof. R. Magini, Officine Galileo, 1940. La figura precedente mostra un esemplare costruito dalle Officine Galileo intorno agli anni ’60.
Bibliografia e note.
La procedura di misura dell`indice di rifrazione con questo strumento si trova in B. Dessau, Manuale di fisica, Vol. II, S.E.L., Milano 1938.
Una descrizione del goniometro, unita ad istruzioni minuziose del suo uso e delle procedure di messa a punto, si trova in E. Perucca, Guida pratica per esperienze didattiche di fisica sperimentale, Zanichelli, Bologna 1937.
E. Perucca, Fisica generale e sperimentale, Vol. I, UTET, Torino 1937.
M. Panitteri – S. Barcio – D. Marucci, Complementi di fisica e laboratorio, G. B. Paravia, Torino 1966; da cui sono tratte la foto in bianco nero le figure IX-2; IX-4; IX-6; IX-7; IX-8 necessarie per le spiegazioni. Per inciso gli autori hanno insegnato al Montani e M.
Panitteri ne è stato Preside.
Scheda n° 14100 delle Officine Galileo Firenze.
Foto di Federico Balilli, elaborazioni, ricerche e testo di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.

 

 

Grande prisma per la riflessione interna totale. Accessorio dell`apparecchio di proiezione della E. Leybold`s Nachfoger, Cöln-Rhein.
Nell`inventario generale n° 6 del 1925, al n°2281/180 si legge: “Provenienza Zambelli Torino. Specchio e prisma a riflessione totale. ₤ 332,60”.
Nell`inventario particolare per categoria n° 7/8 del 1925/1927 al n° 699-2281 si legge di nuovo: “Specchio e prisma a riflessione totale. ₤ 532,60” e si trova nell`elenco degli accessori del proiettore.
Nell`inventario D del 1937, si trova al n° 347 insieme allo specchio 20 × 20 cm in dotazione che ci è pervenuto in buono stato.
    Questo prisma retto serviva per dirigere le immagini sullo schermo a seconda delle esigenze didattiche.
La riflessione interna totale si ha quando il raggio incidente supera l`angolo limite, definito come l`arcoseno del rapporto tra l`indice di rifrazione dell`aria rispetto a quello del vetro.
La riflessione interna totale presenta un assorbimento della luce minore di quella di un buon specchio tradizionale e una maggiore stabilità meccanica.
Nelle foto si è fatto in modo tale che l`osservatore abbia la netta impressione che ci sia un foro nel fondo, mentre in realtà la limpida immagine è dovuta al prisma.
In particolare nella quarta foto si vede parte di una mano molto vicina, mentre nella seconda foto la macchina fotografica mette a fuoco automaticamente l`immagine delle foglie di Monstera Deliciosa che si trovano a qualche metro di distanza.
Ai lati dell`involucro di metallo verniciato in nero vi sono due viti che scorrono su due guide per posizionare il prisma.
Le figure 2132A, 2132F, 2132G, 2132K e 2132L sono tratte dal Catalogue of Physical Apparatus (with descriptions for use) E. Leybold’s Nachfolger Cologne, (Germany) dei primi del Novecento; rinvenibile all’indirizzo:
https://www.sil.si.edu/DigitalCollections/trade-literature/scientific-instruments/files/52546/
Per vedere gli altri accessori dell`apparecchio di proiezione della E. Leybold`s Nachfoger, Cöln-Rhein scrivere: “Rhein” su Cerca.
Foto di Claudio Profumieri, elaborazioni, ricerche e testo di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.

 

 

 

 

 

 

 

 

                         Igrometro Daniell.
Nell`inventario del 1906 a pag. 557, n° 1391, si legge:  “Un igrometro Daniell. Condizione buona. ₤ 8”. Destinato alla Scuola di Chimica e Fisica, Sezione Z16.
Nell`inventario del 1912, si trova al n° 876, prezzo: ₤ 8. Esso fu proposto da J. F. Daniell nel 1820 e serve per misurare l`umidità relativa dell`aria col metodo detto “a punto di rugiada”.
La bolla di vetro sottile (a sinistra nelle foto) ha una fascia dorata e contiene etere per circa 3/4 del suo volume.
Nel liquido è immerso il bulbo di un termometro di portata da -10 °C  a +50 °C con incertezza di 1 °C.
La bolla a destra è ricoperta da una camicia di mussolina.
Le due bolle sono situate alle estremità di un tubo piegato due volte, come si vede nelle foto.
Nell`apparecchio è stato fatto il vuoto.
Il termometro al centro ha una portata da -20 °C a +60 °C con incertezza di 1 °C.
Per la misura si procede nel modo seguente. Si capovolge il tutto e si fa scorrere l`etere nella bolla dorata; poi, dopo aver rimesso in posizione normale lo strumento, si bagna la mussolina con etere che, evaporando, raffredda la bolla situata in alto.
A causa della differenza di temperatura tra le due bolle, l`etere contenuto in quella dorata evapora e va a condensarsi nella bolla più alta. Questo provoca un raffreddamento della bolla dorata.
Si procede in tal modo fino a che compare un velo di rugiada sulla doratura; a questo punto si leggono le temperature segnate dai due termometri.
Infine, consultando apposite tabelle della tensione di vapore saturo, si determina l`umidità relativa ambientale.
Questa misurazione è delicata ed è bene ripeterla più volte di seguito usando particolari accorgimenti.
Bibliografia: M. Panitteri e V. Ruggiero, Esercitazioni di Laboratorio di Fisica, Vol. I, G.B. Paravia & C., 1961.
L`igrometro è esposto al Museo MITI, su proposta di Fabio Panfili.
Foto di Claudio Profumieri, elaborazioni, ricerche e testo di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.

Il baroscopio e la forza di Archimede. Nell`inventario del 1906, pag. 232 n° 821 si legge: ” Baroscopio (rotto il palloncino) £ 10″. Nell`inventario generale del 1923 al n° 12999/24 si trova registrato un baroscopio. Esso serve per mostrare l`effetto della forza di Archimede, dovuta all`aria, sulla misura del peso di un oggetto, ed è essenzialmente una bilancia di piccole dimensioni. Negli esemplari dei primi del Novecento, un braccio, che termina con una vite, ha un cilindretto con madrevite che può essere spostato lungo il braccio stesso; l`altro braccio reca un palloncino cavo in posizione fissa. Questo esemplare manca del palloncino, che si vede nei disegni qui sotto riportati. All`epoca il palloncino era o di metallo cavo molto leggero o di vetro; oggi spesso si usa una sfera di polistirolo. La forza di Archimede, detta impropriamente spinta per consuetudine (la spinta o impulso in fisica è il prodotto di una forza per un tempo), si manifesta quando un corpo è immerso in un fluido. Essa ha il punto di applicazione nel baricentro che avrebbe l`aria se occupasse il volume dell`oggetto, ha un valore uguale al peso che avrebbe un volume d`aria corrispondente al volume dell`oggetto ed è rivolta verso l`alto. Si consiglia per fini didattici di svolgere calcoli e misure quantitative accompagnati alla dimostrazione sperimentale. La forza di Archimede è F = d g V, dove d è la densità dell`aria g è l`accelerazione di gravità e V è il volume del palloncino. Nel caso di un palloncino di forma sferica il volume si trova con V = 4/3 π R³; conoscendo d e g si calcola F . Per eseguire la dimostrazione sperimentale si pone il baroscopio sopra una macchina pneumatica per produrre una buona rarefazione dell`aria. Prima di iniziare è bene togliere sia il cilindretto sia il palloncino per controllare che la bilancia con i soli bracci sia all`equilibrio. Si rimettono al loro posto il cilindretto e il palloncino e si agisce sul cilindretto scorrevole per realizzare l`equilibrio, poi si poggia la campana di vetro sulla macchina con dentro il baroscopio ( vedi la figura sotto).

Man mano che l`aria viene tolta si osserva che la bilancia perde l`equilibrio e pende sempre di più dalla parte del palloncino. Si ferma allora la macchina per mostrare che l`abbassamento del palloncino non è dovuto alla macchina che porta via l`aria, poi si immette lentamente l`aria per far vedere che l`equilibrio si ristabilisce.

Sempre per spiegare quantitativamente ciò che si è mostrato bisogna pesare con buona precisione il cilindretto e il palloncino. Ad essere pignoli si dovrebbe misurare anche il volume del piccolo cilindro di metallo per non trascurare anche la piccola forza di Archimede che agisce su di esso, ma per ragioni di semplicità possiamo tralasciare questo particolare a causa del piccolo volume dell`oggetto confrontato col volume del palloncino.

Chiamando `a` la distanza tra il cilindretto e il fulcro e `b` la distanza tra il punto in cui è appeso il palloncino e il fulcro, `p` il peso del disco e `P` quello del palloncino, scriviamo la condizione di equilibrio in presenza d`aria: p · a = (P – F) · b. Misuriamo con accuratezza `a` e `b`! Quando il baroscopio è dentro la campana e in aria rarefatta, la F diventa trascurabile e così il suo momento, dunque l`equilibrio viene a mancare. Nel vuoto il palloncino “appare” più pesante che nell`aria dove è “sostenuto” dalla forza di Archimede. Gli allievi dovrebbero infine dedurre che, quando è richiesta una buona precisione nelle misure di massa di oggetti di discrete dimensioni fatte in presenza d`aria, la forza di Archimede introduce un errore non trascurabile. Il primo disegno è tratto dal Revised and Illustrated Catalogue N° 10 Physical Instruments di F. Ernecke Berlin S. W. dei primi anni del Novecento; il secondo è tratto dal Priced and Illustrated Catalogue of Physical Instruments di J. W. Queen & CO. della stessa epoca. Il baroscopio fu inventato da Otto von Guericke (1602 – 1686).

Foto di Claudio Profumieri, elaborazioni, ricerche e testo di Fabio Panfili.