Categoria: fisica

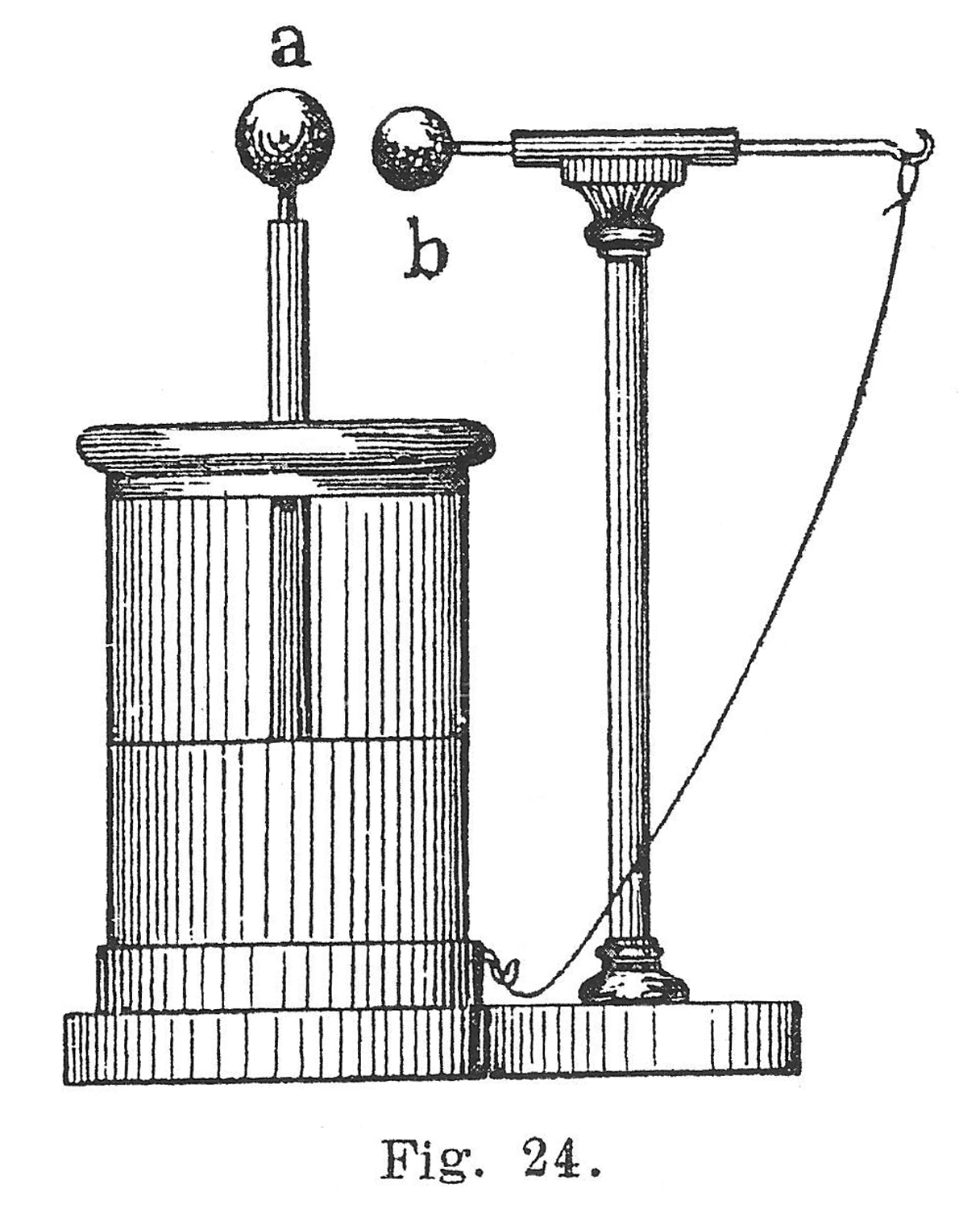
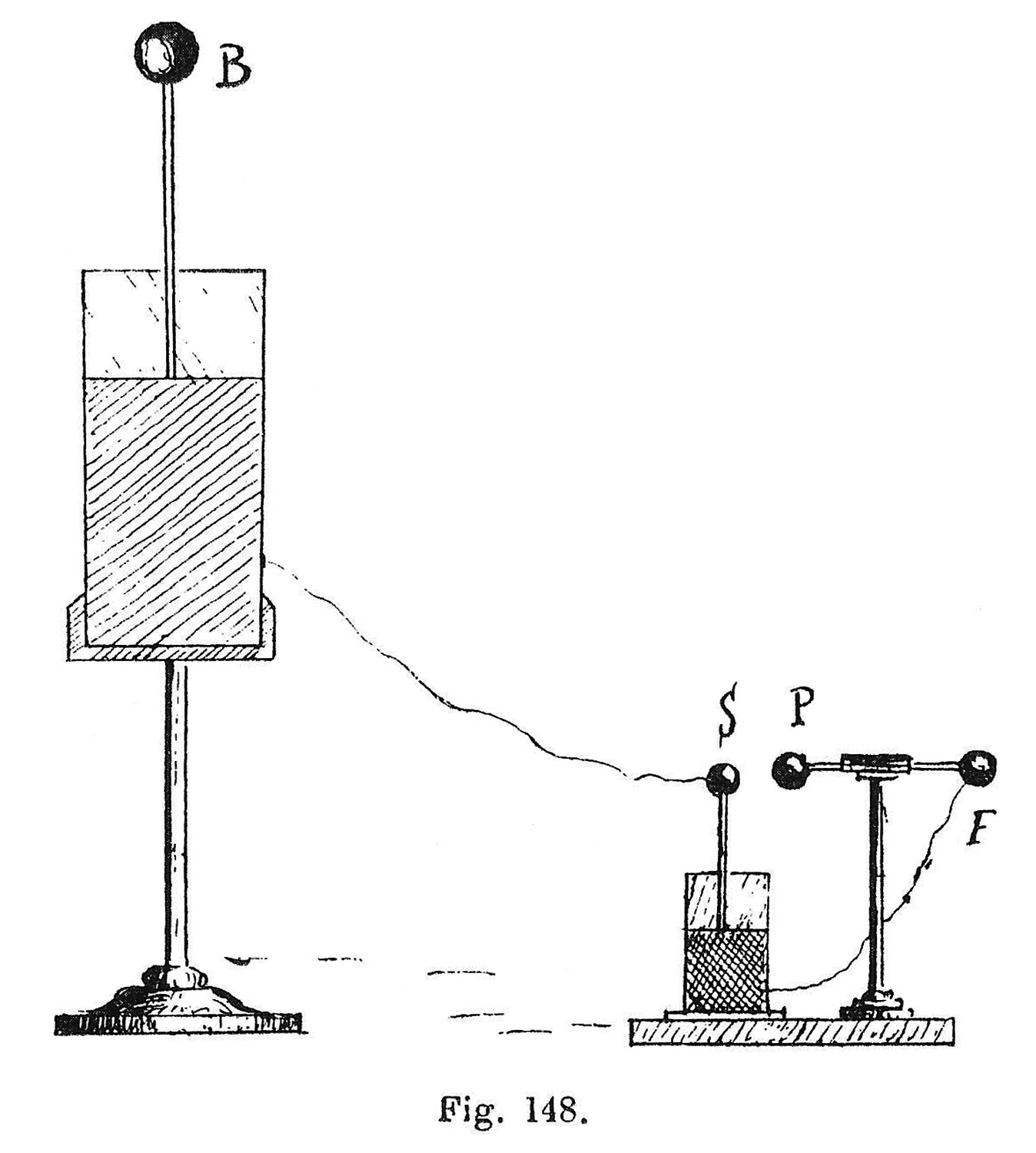
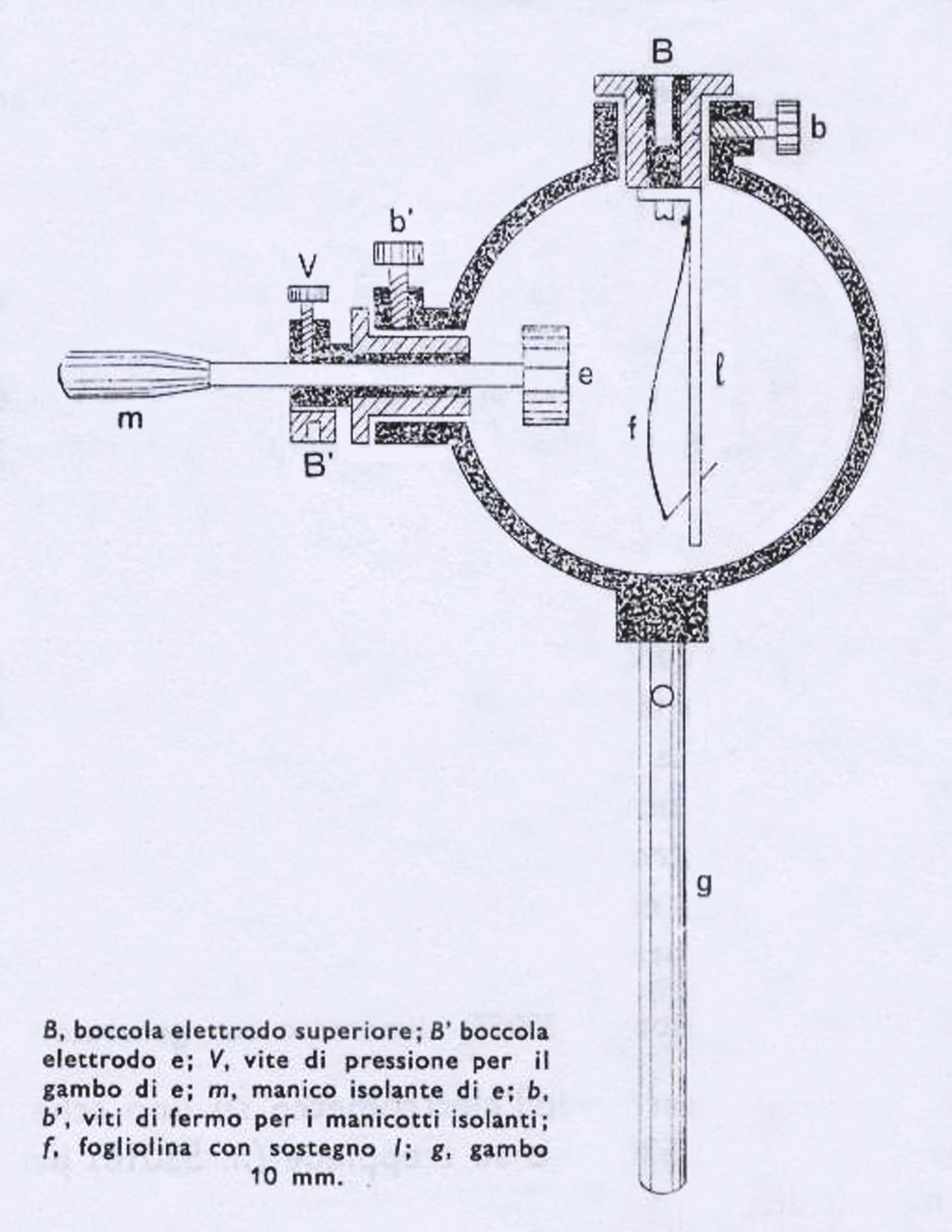
Elettrometro simile al tipo assoluto Braun della E. Leybold`s Nachfolger A. G. Colonia.
La presunta epoca di acquisto di questo particolare elettrometro è stata dedotta dall`aspetto, dall`esame dei materiali impiegati e dallo stile delle scritte; inoltre nelle schede di istruzioni della casa costruttrice, risalenti agli anni 1956-1962, un elettrometro del tipo Braun si trova spesso associato a quello di Wulf.
Si può pensare dunque che sia stato acquistato qualche anno prima del 1937, se corrisponde al n° 389 dell`inventario D del 1937, oppure poco tempo dopo e che non sia stato riportato negli inventari.
Questo modello non compare in nessun catalogo di strumenti in possesso del Montani e in nessuno dei numerosi cataloghi consultati.
Nelle foto sono stati  tolti o il pannello anteriore o quello posteriore per farne vedere i particolari costruttivi.
L`elettrometro indica o la carica prelevata per contatto dall`oggetto in esame o la presenza di oggetti carichi nelle vicinanze per induzione elettrostatica.
Inoltre, se opportunamente tarato, può misurare una differenza di potenziale.
Fra quelli esistenti al Montani questo elettrometro è il più antico, sensibile e affidabile nelle indicazioni.
L`ago sottile, leggero e ben bilanciato, gira intorno ad un perno orizzontale costituito da un filo sottilissimo; agendo su questo si può regolare la posizione dell`ago in modo tale che, a riposo, esso giace vicino a una lastrina metallica fissa.
Quando l`elettroscopio viene caricato, l`ago assume una posizione di equilibrio dovuta agli effetti della forza di repulsione elettrostatica fra l`ago e la lastrina e della componente non bilanciata del suo peso.
L`angolo che forma l`ago con la lastrina dipende in modo non lineare dal numero di cariche presenti sui due oggetti. L’elettrometro ha una piccola capacità e, quando assume cariche in eccesso, indica, entro una larga approssimazione, la differenza di potenziale elettrostatico raggiunto dall’elettrodo rispetto alla carcassa.
La piccola variazione della sua geometria non ne cambia apprezzabilmente la capacità, piuttosto vi sono altri fattori che lo rendono poco affidabile nella misura.
L’esperienza infatti mostra che il funzionamento degli elettrometri è molto capriccioso per farne uno strumento di misura vero e proprio: risultano critiche sia l’umidità dell’aria (che se eccessiva lo scarica rapidamente), sia la geometria e la natura degli oggetti vicini. La carcassa di metallo fa da schermo ma non è sufficiente ad evitare queste influenze. Una taratura delicata può rendere la misura quantitativa, ma, ad esempio, una mano che si avvicina può mutare la divergenza dell’ago.
L`uso didattico prevalente di tale strumento, oltre a rilevare la presenza di cariche, è il riconoscimento del loro segno, inoltre serve per mostrare l`induzione elettrostatica, il funzionamento della gabbia o del pozzo di Beccaria-Faraday, e negli esperimenti col condensatore di Epino, con le Bottiglie di Leyda, con l`elettroforo di Volta ecc.

La figura 135 dell’elettrometro di Braun è tratta da pag. 232 di A. Battelli e P. Cardani, Trattato di Fisica sperimentale, vol. IV, F. Vallardi edit., Milano 1925 ed è quasi identica alla figura 5532.

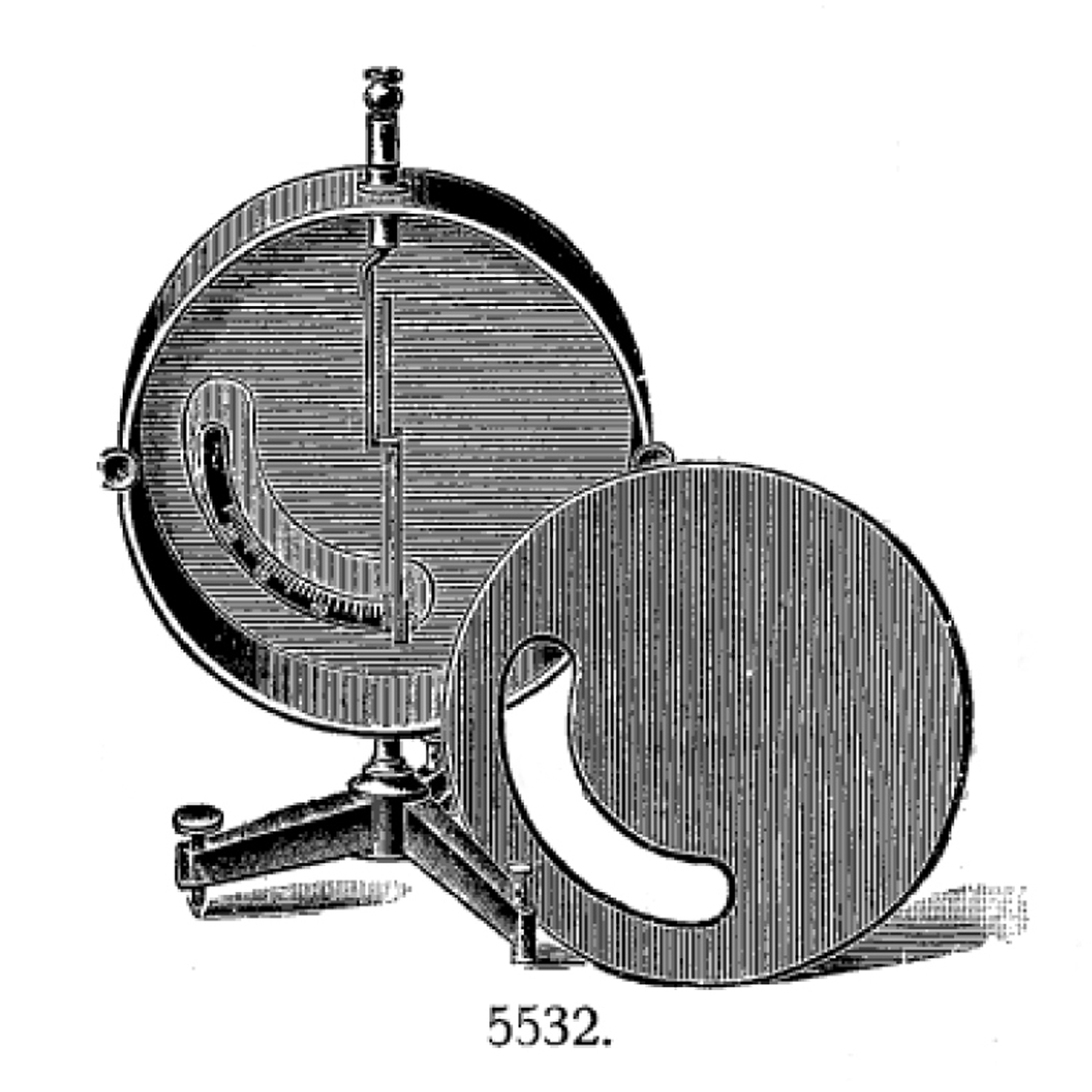
Figura che è a pag. 543 del Catalogue des Appareils pour l’Enseignement de la Physique construit par E. Leybold’s Nachfolger Cologne, 1905. Che si trova all’indirizzo:
http://cnum.cnam.fr/PDF/cnum_M9915_1.pdf .

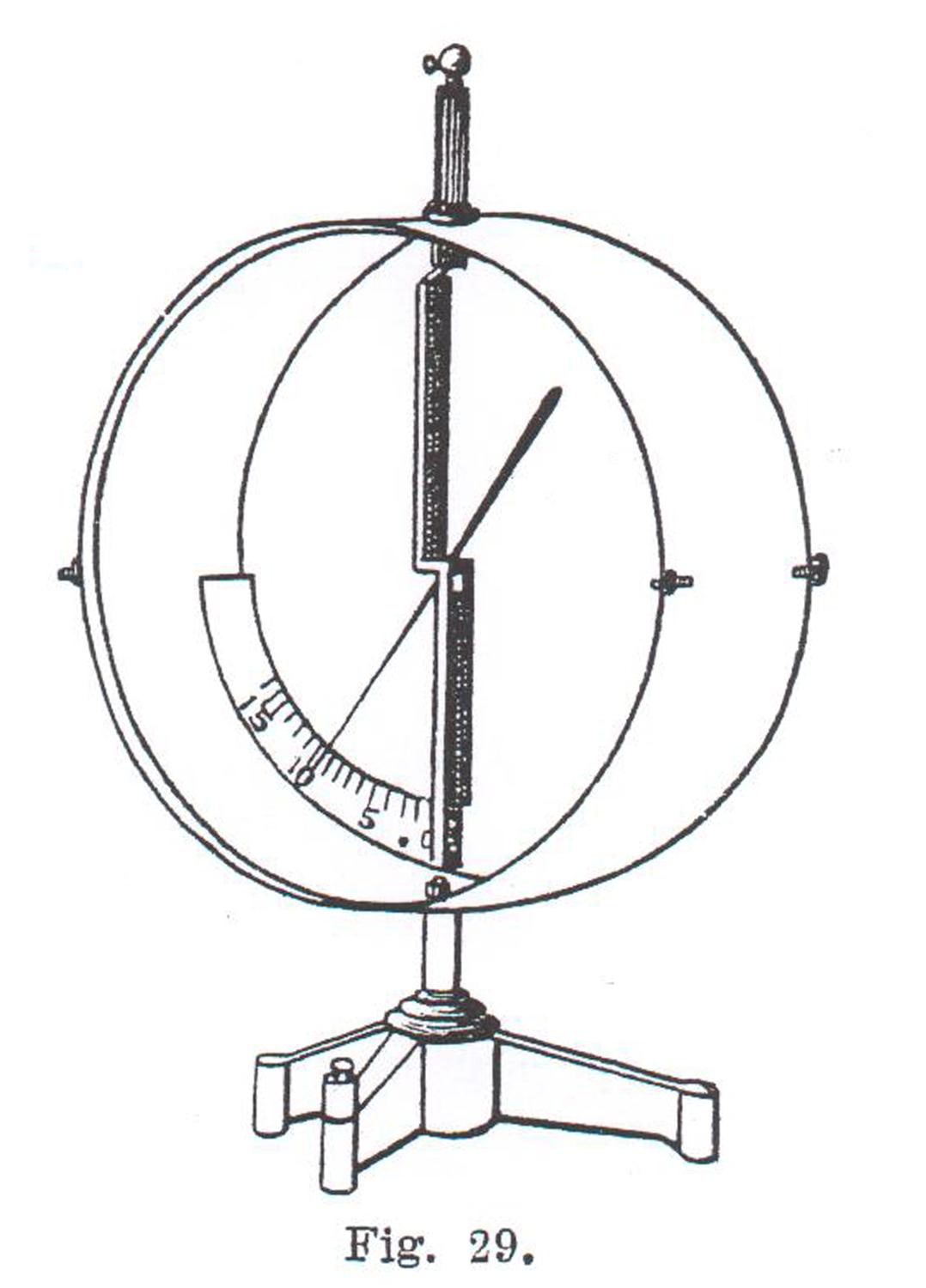
La figura 29 è tratta da B. Dessau, Manuale di fisica, vol. III S.E.L Milano 1935.

La figura 7 è a pag. 18 di Die Elektrizität und Ihre Anwendungen von Dr. L. Graetz Stuttgart Velag von J.
Engelhorn 1906; che si trova algli indirizzi:
https://archive.org/details/dieelektrizittu00graegoog/page/n29/mode/2up
https://ia802604.us.archive.org/21/items/dieelektrizittu00graegoog/dieelektrizittu00graegoog.pdf
L’elettrometro è esposto al Museo MITI, su proposta di Fabio Panfili.
La foto con lo strumento poggiato su un panno rosso è di Daniele Maiani e lo strumento è visto dal retro.
Foto di Claudio Profumieri, elaborazioni, ricerche e testo di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.

 

 

 

 

 

        Elettrometro di Lane.
Della ditta A. Dall`Eco Ing. Santarelli successore, Firenze.
Nell`inventario del 1912 a pag. 64 n° 1074 si legge: “Bottiglie di Leyda”.
Nell`inventario del 1919 al n° 964/30 si legge: “Bottiglia di Leyda con spinterometro regolabile su base di legno, Ing. Santarelli” che corrisponde a una descrizione sintetica dell`esemplare del Montani.
L`elettrometro di Lane serve per una misura relativa della carica fornita ad esempio da una bottiglia di Leyda o da una macchina elettrostatica ecc.
Esso è costituito da una piccola bottiglia di Leyda, la cui armatura esterna comunica con un`asta metallica che termina in una sferetta.
Di fronte a questa vi è un`altra sferetta connessa all`armatura interna.
La distanza tra le sferette è regolabile.


 La scintilla tra le due sferette, di due cm di diametro ciascuna, avviene quando si raggiunge una certa differenza di potenziale, nell`aria secca infatti occorre una tensione V di circa 32 kV per ogni centimetro di distanza tra di esse, a pressione atmosferica e temperatura standard *(nota 1). Quanto detto può far concludere che una scintilla trasferisca tra le armature della bottiglia una quantità di cariche
Q = C V,
dove C è la capacità della bottiglia di Lane.
Ma è noto che il fenomeno disruptivo è molto complesso: basti dire che la prima scintilla richiede una maggiore differenza di potenziale della successiva, anche se tutti gli altri parametri sono rimasti invariati, poiché l`aria presenta una ionizzazione residua che facilita la scarica.
Pertanto nella letteratura si raccomanda ai fini del conteggio delle scintille, di scartare le prime. Con una certa approssimazione, si può comunque affermare che, ad ogni scintilla, passi, attraverso il filo che connette lo spinterometro all`armatura esterna, una quantità costante di elettricità.

Descriviamo qui brevemente la disposizione più importante con l`impiego della bottiglia di Lane: la misura della carica accumulata da un condensatore, o meglio da una bottiglia di Leyda.

Il polo positivo di una macchina elettrostatica viene collegato all`armatura interna della bottiglia in esame, mentre il negativo va a terra. Si connette quindi l`armatura esterna con quella interna dell`elettrometro di Lane e l`armatura esterna di questo va unita sia con l`astina regolabile dello spinterometro sia con la terra. Questa connessione viene detta in serie: la stessa quantità di cariche che si accumula nella bottiglia in esame si affaccia tra le armature della bottiglia di Lane.
All`aumentare delle cariche cresce la differenza di potenziale tra le due sferette, quando questa raggiunge il valore critico avviene la scintilla, la bottiglia di Lane si è scaricata mostrando che una quantità di cariche Q si è depositata sulla bottiglia in esame.
Subito dopo la bottiglia di Lane inizia la ricarica e il processo si ripete. Si nota ben presto che le scintille diventano via via meno frequenti poiché il condensatore in esame sta completando la sua carica.
Il conteggio delle scintille fornisce una valutazione relativa delle cariche accumulate.
Condizione necessaria per il buon funzionamento di questo sistema di misura è che la capacità della bottiglia di Lane sia più piccola di quella da esaminare, altrimenti può accadere che quest`ultima raggiunga più rapidamente una differenza di potenziale critica tale da far scoccare la scintilla fra i suoi terminali, piuttosto che allo spinterometro di misura, ancorché le sferette di questo siano molto vicine.
Nota 1: vi sono apposite tabelle in proposito.
Bibliografia: B. Dessau, Manuale di fisica-elettrologia, Vol. III, SEL, Milano 1931, da cui è tratta la figura 24.
A. Battelli e P. Cardani, Trattato di Fisica Sperimentale, Vol. IV, F. Vallardi, Milano 1925, da cui è tratta la figura 148.
Scheda di istruzioni della ditta Galileo di Firenze. L. Olivieri ed E. Ravelli, Elettrotecnica-Misure Elettriche, Vol. III, CEDAM, Padova 1962.
La figura N 1065 è a pag. 256 del catalogo: Apparecchi per l’Insegnamento della Fisica a cura del prof. R. Magini, Officine Galileo, 1940.La figura 5819 è a pag. del Catalogue des Appareils pour l’Enseignement de la Physique construit par E.
Leybold’s Nachfolger Cologne, 1905; che si trova all’indirizzo:
http://cnum.cnam.fr/PDF/cnum_M9915_1.pdf
Foto di Federico Balilli e di Ilaria Leoni, elaborazioni, ricerche e testo di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.

 

 

 

 

  Elettroscopio di Wulf. Prima parte.
Costruito dalla E. Leybold`s Nachfolger n° 2841 D.R.P., Köln.
Inventario D del dicembre 1941, n° 1086.
Ditta fornitrice Ing. Barletta, Milano, (N° 5626).

ABSTRACT: Wulf’s electroscope. Dated 1941; manufactured by the company E. Leybold’s
Nachfolger A. G. ; Cologne Germany. Through a complex method of calibration, the device allows to
measure the amount of charge present in every “drop” and then to measure the total charge of the
charged body under examination. To measure the amount of electricity in a capacitor set at a specific
voltage, you must connect one of its armatures with the stem “g” and the electrode “e”, and the other
armature with the upper electrode by means of a wire and a very high resistance. We can observe that
the little leaf  “f” , connected at the bottom to a quartz spring clip is attracted by the electrode “e”,
when it touches the electrode the leaf loses its charge and falls, then recharges and it is attracted again
and after a new contact it falls again and so on. If  “q” indicates the small charge lost (drop) with each
contact and “n” represents the number of contacts, at the end of the process we can say that, with a
slight approximation, the charge Q of the capacitor is:
Q = q n .
Traduzione di Alex Vlasovs, supervisione della prof.ssa Meri Biancucci.
L`elettroscopio di Wulf  (detto nell`inventario del 1941 elettroscopio universale) deriva dall`elettrometro a scarica di Gaugain, che è un elettroscopio a foglie d`oro con accanto a una di esse una lastrina di metallo collegata a terra; ogni volta che la carica sulla fogliolina raggiunge un valore determinato, questa diverge fino a toccare la lastrina scaricando l`elettroscopio.
È risultata parzialmente infruttuosa la ricerca degli accessori elencati nell`inventario.
Per consultare la scheda relativa a un condensatore, usato  probabilmente come accessorio dell’elettroscopio di Wulf per la misura di corrente, scrivere “Schott” su Cerca.

L`astina con relativa fogliolina metallica è stata rinvenuta nel 2004 dal tecnico del laboratorio di fisica Federico Balilli e sostituisce l`originale. Il ricambio probabilmente faceva parte della dotazione primitiva.
La figura 1 di questo delicato equipaggio è stata tratta dalla scheda n° 3/36 CD 537.721;a del 1962 edita dalla casa costruttrice; la parte superiore del sottilissimo foglio di alluminio è fissata all`astina, e viene tesa in basso da un fermaglio elastico di quarzo, estremamente sottile, di forma circolare (quasi invisibile a occhio nudo).
L`oro si può ridurre in striscioline quasi trasparenti, ma l`alluminio ha un peso specifico molto minore.
Quando la forza elettrica supera quella elastica del fermaglio di quarzo, la fogliolina va a toccare l`elettrodo scaricandosi.
La lente serve per osservare meglio il comportamento della fogliolina nel processo di scarica. Tra gli accessori c`era un proiettore per mostrare il processo di scarica alla classe.
Un elettrometro di T. Wulf (1868-1946) più antico (1909), sostanzialmente diverso nel principio di funzionamento, usava due fili di quarzo metallizzati come foglie, tesi da un lievissimo anello di quarzo, che, osservati al microscopio, fornivano indicazioni fino a un volt.

Si osservi la figura, tratta dalla Scheda di Istruzione N. 424 della Paravia, che rappresenta l’apparecchio
in sezione.
La boccola “B” fa parte dell`elettrodo su cui è sospesa la fogliolina metallica. Di fianco (a sinistra nella figura) è applicato l`altro elettrodo “e” a testa circolare. Questo può essere spostato in modo da avvicinarlo o allontanarlo dalla fogliolina mobile, agendo così sulla sensibilità dello strumento. Se si vuole misurare la quantità di elettricità posseduta da un condensatore, si deve collegare una sua armatura con il gambo “g” e l`elettrodo “e”. Poi si carica il condensatore con una tensione nota, infine si collega l`altra armatura con l`elettrodo superiore per mezzo di un filo e di una resistenza molto elevata (di almeno 50 MΩ). Si osserva che la fogliolina “f”, respinta dall`astina a cui è appesa, viene attratta dall`elettrodo “e”, lo tocca, si scarica e poi ricade; viene di nuovo attratta e dopo un altro contatto ricade e così via. Questo processo in gergo si chiama: “a goccia a goccia”. Se q è la piccola carica perduta ad ogni contatto ed n è il numero di contatti, all`esaurirsi del processo si può dire, con una certa approssimazione, che la carica del condensatore è:
Q = q n .
La resistenza serve a evitare che avvenga subito una scarica troppo intensa che potrebbe bruciare la fogliolina.
La misura descritta non ha senso se non si conosce la quantità q. Ciò si può fare, non senza approssimazioni e difficoltà, col procedimento di taratura dell`elettrometro.
Si prende un condensatore di cui sia nota la capacità e dunque
Q = V C,
essendo noto V, si trova Q. Pertanto si può ricavare q dall`espressione:
q = Q/n.
Purtroppo questa taratura vale solo per la distanza tra l`elettrodo “e” e la fogliolina “f” usata nell`esperienza. Esiste una trattazione più rigorosa dei fenomeni descritti (scheda 3/36 del 1962 della casa costruttrice) riportata nelle figure della terza parte.
Tutto quanto si è detto dà un`idea della delicatezza richiesta dall`impiego di questo strumento, non adatto alle moderne esigenze didattiche.
Bibliografia.
L’elettrometro a scarica di Gaugain è brevemente descritto da O. Murani in Trattato elementare di Fisica, vol. II, U. Hoepli, Milano 1933.
Un più antico elettrometro di Wulf, sostanzialmente diverso, viene descritto sia da G. Goretti Miniati,
Elementi di Fisica, vol. II, F. Cuggiani, Roma 1909, sia da E. Perucca, Fisica generale e sperimentale, vol. II, UTET, Torino 1934.
Per consultare le altre parti scrivere: “Wulf” su Cerca.
L`elettroscopio di Wulf è  esposto al Museo MITI, su proposta di Fabio Panfili.
Foto di Federico Balilli, Daniele Maiani e Claudio Profumieri, elaborazioni, ricerche e testo di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.

 

 

 

 

 

Elettroscopio di Wulf. Seconda parte.
Costruito dalla E. Leybold’s Nachfolger n° 2841 D.R.P. Köln.
Inventario D del dicembre 1941, n° 1086. Ditta fornitrice Ing. Barletta, Milano, (N° 5626)
Diamo qui un elenco di alcune applicazioni sperimentali dello strumento:
1) Determinazione della capacità dell`elettroscopio stesso per la sua taratura prima delle misure;
2) Misura dell`intensità dei raggi X;
3) Effetto fotoelettrico;
4) Rivelazione di particelle alfa e beta.
Oggi le prove 2) e 4) sono proibite per legge nelle scuole.

Inoltre riportiamo la scheda N. 424 pubblicata dalla Paravia.Ciò che desta meraviglia è l`acquisto in quell`epoca di un tale delicato e complesso strumento.
Per consultare le altre parti scrivere “Wulf” su Cerca.
L’elettroscopio di Wulf è esposto al Museo MITI, su proposta di Fabio Panfili.
Foto di Claudio Profumieri, elaborazioni, ricerche e testo di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.

 

 

 

 

Dispositivo elettromagnetico bifase a campo rotante per tubo di Braun.
Nell`inventario generale n° 6 degli anni 1925-1927, al n° 2714/229 si legge: “Dispositivo per campo magnetico rotante per il tubo di Braun; ₤ 15; Fisica” acquistato nel 1927.
Un tubo di Braun infatti è citato nella stessa pagina al n° 2706/221. Di questo tubo non si hanno altre notizie.
Nella collezione del Montani esistono due dispositivi elettromagnetici per il tubo di Braun risalenti alla stessa epoca e non si sa a quale dei due si riferisca l`inventario del 1926 – 1927; mentre nell`inventario D del 1937 sono citati entrambi come già esistenti: infatti al n° 87 si legge:  “Modello dimostrativo per campo rotante bifase – Kohl – ₤ 200”. Prima destinazione Lab. Misure Elettriche; e al n° 86 si legge: “Modello dimostrativo per campo rotante trifase – Kohl – ₤ 200”. Prima destinazione Lab. Misure Elettriche.
Quest’ultimo si può vedere nella sezione di Fisica.
Questo dispositivo è identico a quelli che si trovano nei cataloghi della Max Khol Chemnitz dei primi anni del Novecento, come si può vedere nella figura 61502a che si trova a pag. 898 del catalogo Price List No 50 Vols. II and III Physical Apparatus Vol II Max Khol A.G. Chemnitz [1909-11?]; rinvenibile all’indirizzo:
https://ia802605.us.archive.org/4/items/pricelistno5023kohlrich/pricelistno5023kohlrich.pdf .

Dalla pagina 899 del catalogo abbiamo tratto (con lieve modifica) anche la scritta dedicata al tubo di Braun disegnato nella figura 61502 che è rappresentato da solo nella figura 61499 di pag. 898.
Il campo elettromagnetico rotante bifase fu scoperto nel 1885 da G. Ferraris, fisico e ingegnere piemontese (1847-1897), nell`autunno di quell`anno dimostrò pubblicamente che, disponendo due bobine perpendicolarmente tra loro e facendole percorrere da due correnti alternate di ugual valore e sfasate a 90°, si generava, nello spazio compreso tra esse, un campo magnetico rotante.
Il campo magnetico provoca su un elettrone in moto una deviazione (nella didattica si usa la regola della mano sinistra); se il campo magnetico è rotante, anche la deviazione sugli elettroni provenienti dal catodo subisce una continua rotazione. Rotazione che appare sullo schermo disegnando ad esempio un cerchio.
Questo dispositivo serviva dunque per la deviazione degli elettroni nel tubo mediante il campo magnetico generato dalle due bobine, che potevano essere alimentate o con correnti continue, o meglio con correnti alternate, opportunamente sfasate tra loro, per ottenere sullo schermo le figure dovute agli effetti dinamici della combinazione dei campi magnetici variabili. Si potevano ottenere in tal modo le figure di Lissajous, agendo sulle fasi e sui valori delle due correnti. Ovviamente si poteva alimentare una sola bobina in C.C. o in C.A.; oppure osservare gli effetti che si ottenevano spostando una delle due bobine in varie posizioni. Ognuna di esse reca la scritta 0,1 ohm. La bobina mobile è fissata ad un anello che scivola sull`altro fisso dopo aver allentato la vite ben visibile sulla destra nella prima foto; mentre per spostare eventualmente l`altra bobina bisogna intervenire sulle tre piccole viti che la tengono stretta all`anello fisso.
Foto di Claudio Profumieri, elaborazioni, ricerche e testo di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.