

 Arganetto idraulico.
Arganetto idraulico.
Nell`inventario del 1919, a pag. 37 n° 834/12, si trova elencato fra diversi oggetti del Gabinetto di Fisica, il suo costo era di ₤ 25. Ne ignoriamo il costruttore poiché l`oggetto probabilmente è stato riverniciato.
Alcuni autori ne attribuiscono l`invenzione a J. A. Segner (1704 – 1777), che in effetti nella sua turbina ad acqua usò lo stesso genere di ugelli; altri indicano J. T. Desaguliers (1683 – 1744).
Il suo funzionamento si basa su due principi della fisica: la trasformazione dell`energia potenziale in cinetica e il cosiddetto principio di azione e reazione (che sarebbe meglio chiamare principio di interazione).
Bisogna subito dire che non tutta l`energia potenziale diventa cinetica per le inevitabili perdite e che nella didattica non è molto chiaro cosa si intende per “azione” e per “reazione”.
Il mulinello è costituito da un`ampolla di vetro che viene riempita d`acqua; nella sua parte superiore vi è una tazza di metallo aperta per immettere l`acqua e con un incavo al centro che ben si adatta alla punta conica di una vite fissata sul sostegno che ne regola l`altezza (come si vede in una foto).
Nella sua parte inferiore invece vi è una tazza che presenta quattro tubicini sagomati in modo tale da permettere la fuoriuscita dell`acqua nello stesso verso; anche questa tazza sotto ha un dispositivo per la rotazione dell`ampolla intorno al suo asse di simmetria verticale con attriti molto bassi.
La vite nella parte superiore consente di togliere l`ampolla con facilità dal contenitore di metallo e regola anche la distanza del cono dall`appoggio per una rotazione ottimale. La parte inferiore dell`arganetto è costituita da un contenitore che evita lo spruzzamento dell`acqua nell`ambiente durante la dimostrazione, esso è munito di uno scarico che non fa accumulare il liquido nel contenitore stesso, accumulo che impedirebbe il normale voluto deflusso veloce dell`acqua dai quattro tubicini.
Dunque, per semplificare la spiegazione, trascuriamo sia le perdite di energia sia la velocità di abbassamento del livello superiore dell`acqua contenuta nell`ampolla e affermiamo che l`energia potenziale dell`acqua, dovuta al dislivello tra il pelo libero dell`acqua e gli ugelli di uscita, si trasforma in energia di pressione nella parte più bassa, secondo il noto teorema di Bernoulli sulla conservazione dell`energia per i liquidi ideali in moto stazionario, e ancora che questa energia si trasforma in energia cinetica dando luogo ad una certa velocità di efflusso dell`acqua.
Con queste approssimazioni si potrebbe dire che la velocità di uscita è pari alla radice quadrata di 2 g h, dove g è l`accelerazione di gravità del luogo e h è il dislivello.
A questo dispositivo non si può applicare facilmente il principio della conservazione del momento della quantità di moto poiché la massa dell`intero sistema diminuisce nel tempo, pur senza considerare le perdite per attriti e altri aspetti. Ma, per spiegare “l`azione e la reazione”, consideriamo un intervallo di tempo sufficientemente breve (diremmo meglio infinitesimo) tale da “fingere” di poter trascurare la diminuzione della massa totale d`acqua.
Allora il momento della quantità di moto della massa d`acqua che esce dai quattro tubicini in quell`intervallo di tempo deve equivalere al momento della quantità di moto dell`intera ampolla con il suo contenuto, e dunque quest`ultima deve ruotare in senso opposto al verso della velocità di efflusso dell`acqua per conservare la quantità di moto totale del sistema!
Ulteriore complicazione nel voler applicare il principio della conservazione del momento della quantità di moto vien dal fatto (già suggerito) che la velocità di efflusso nel tempo diminuisce col diminuire del dislivello dell’acqua. Nella realtà, al solito, le cose sono molto più complicate di come apparirebbe solo a vedere l`arganetto in funzione, ma nella scienza le cose vanno sempre così.
Chi parla di scienze esatte, non conosce veramente le scienze.

La figura sopra è tratta da L. Segalin, Fisica sperimentale, Vol. I, G. B. Paravia & C., Torino 1933.
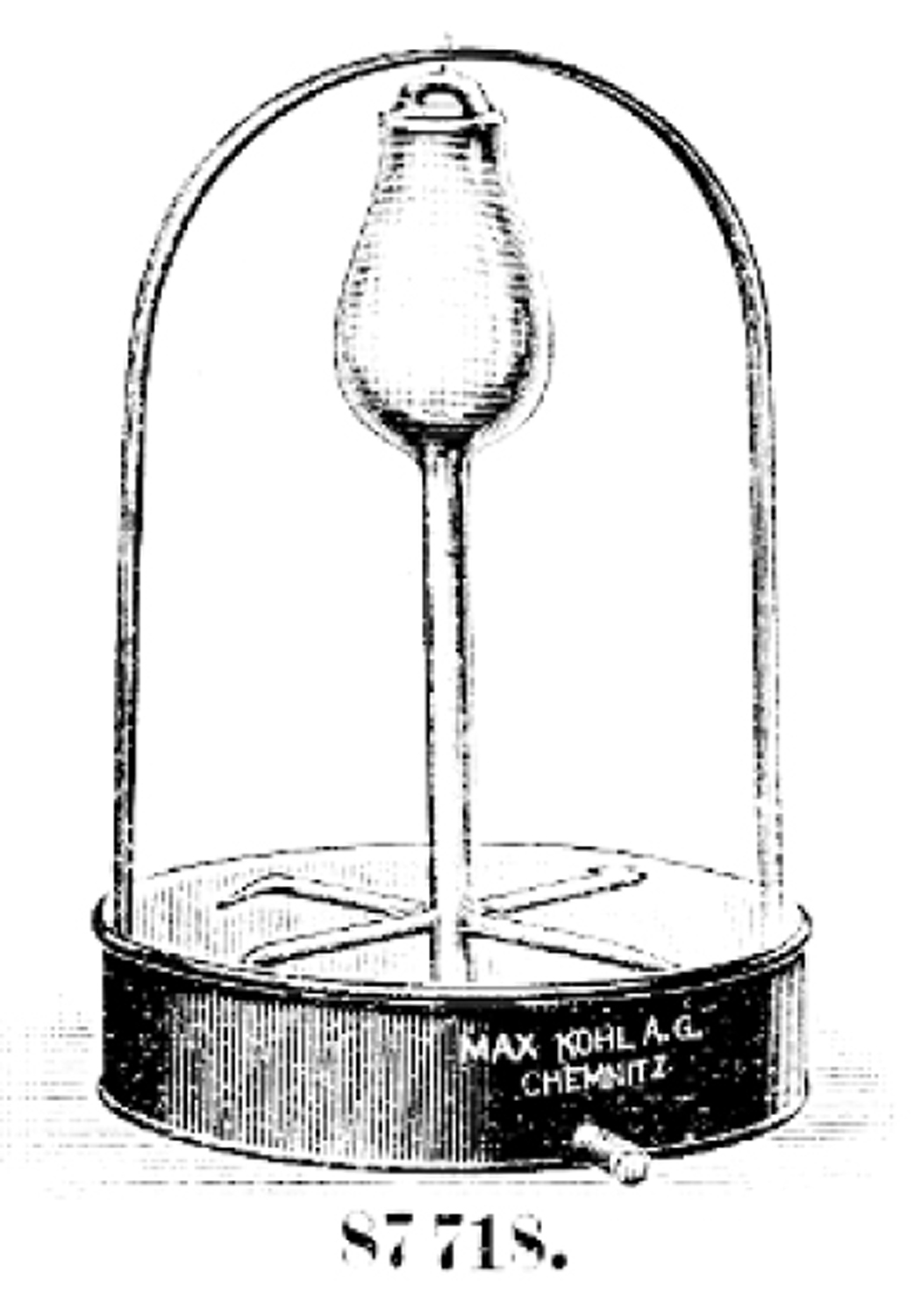
La figura 87718 è a pag. 308 del catalogo Preiliste Nr. 100, Band II. Physikalische Apparate Max Kohl
Chemnitz [1928?], rinvenibile all’indirizzo:
https://vlp.mpiwg-berlin.mpg.de/library/data/lit21057?
Tra quelli riportati dai cataloghi più noti dell’epoca, l’esemplare della Max Kohl è il più somigliante a
questo esemplare.
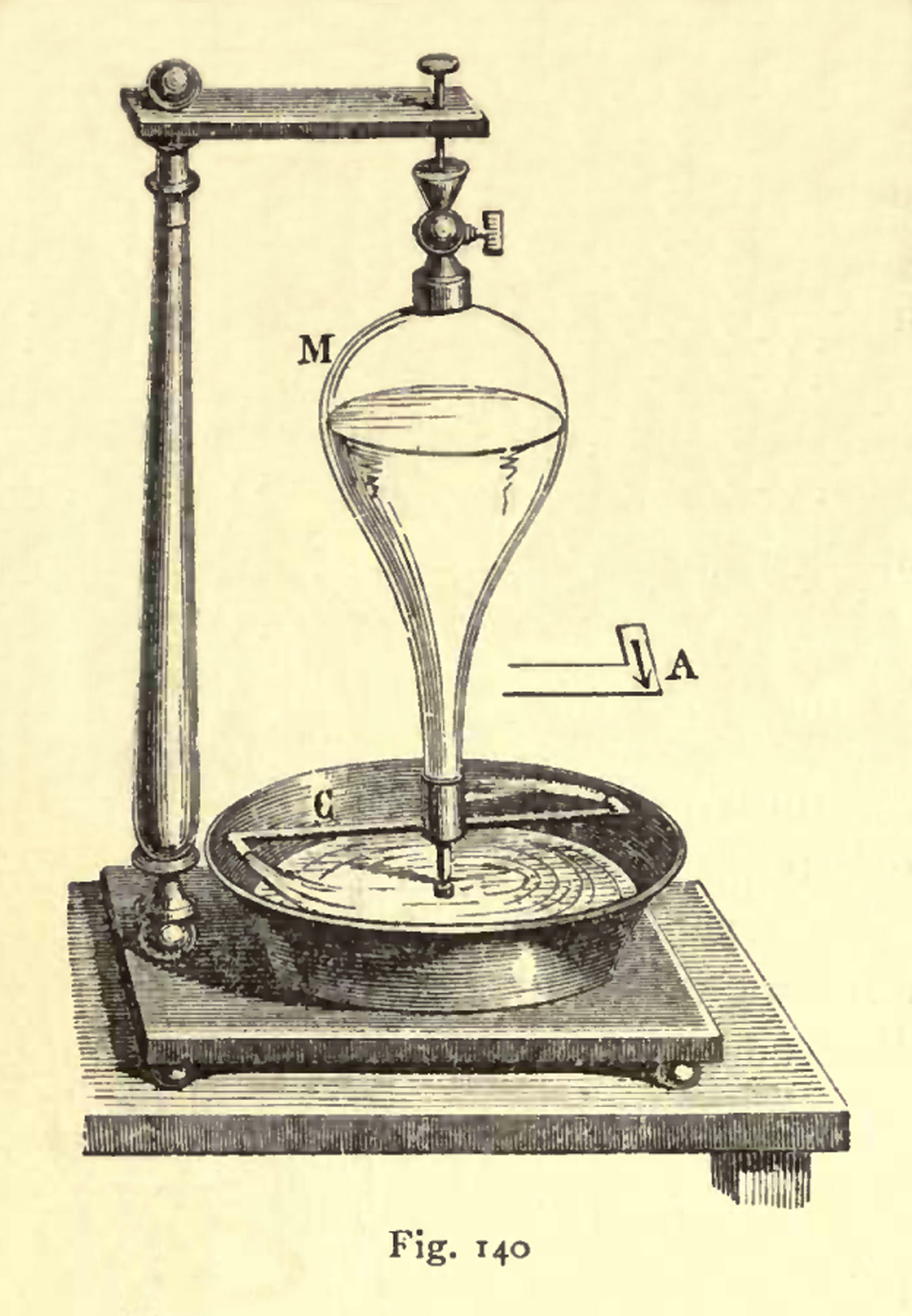
La figura 140 è a pag. 140 di Elementary Treatise on Phisics Experimental and Applied transalted from
Ganot’s Éléments De Physique by E. Atkinsons, W. Wood & Co. New York 1910, rinvenibile
all’indirizzo:
https://archive.org/details/treatphysics00ganorich .
Nelle ultime due foto i tubicini sembrano mossi poiché l’arganetto è in moto.
Foto di Claudio Profumieri, elaborazioni, ricerche e testo di Fabio Panfili.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.



